|
Robert J Casson DPhil FRANZCO and Lachlan DM Farmer MBBS
Clinical and Experimental Ophthalmology 2014; 42: 590–596 doi:
10.1111/ceo.12358
摘要
如果使用得當,線性迴歸 (LR)
是一種強大的統計模型。由於該模型是任何事件的長期序列的近似值,因此需要對其所代表的數據保持適當假設。然而,這些假設經常被誤解。我們介紹了
LR 模型中使用的基本假設,並提供了一種簡單的方法來檢查它們在使用前是否得到滿足。這樣做的目的是提高
LR 在研究中的有效性和適用性。
介紹
本質上,所有模型都是錯誤的,但有些模型是有用的。(Essentially, all models
are wrong, but some are useful. George Box)
統計模型是用數學語言表達的對現實的簡化。為了實現這種簡化,所有統計模型都做出假設。線性迴歸 (LR)
也不例外。如果使用得當,LR
是一種強大的統計工具,可以解釋和預測現實世界的現象,但對其假設的誤解可能會導致錯誤和誤導性的結論。許多研究人員對
LR 的假設存在誤解,尤其是所謂的“常態假設”。這種混淆可能部分是由於各種文章和網路資源中關於
LR 基礎假設的不一致的描述造成的。
在此針對臨床研究人員的目標讀者討論 LR
的數學基礎及其假設。提出了一種簡單的方法來檢查這些假設在應用 LR
之前是否得到滿足,並且這種滿足在統計方法的討論是否被例行報告。首先簡要討論相關性。
相關性
相關性和迴歸是變數之間關聯的度量。相關性描述了兩個隨機變數之間線性關係的強度,即 -1 和
1 之間的單個較小單位值(表示為 r;相關係數)。如果
r = 0,則兩個變數之間沒有關係(它們是獨立的)。如果它是正的,那麼當一個變數呈上升趨勢時,另一個變數也呈上升趨勢。如果它是負數,那麼作為一個變數趨勢向上,另一個趨勢向下。還有其他重要的區別:它僅在考慮兩個隨機變數時使用;沒有繪製最佳配適線,也沒有暗示一個變數可以預測另一個變數。兩個變數都是研究人員量測的和不受控制的,即X和Y都是隨機變數;與迴歸相反,在迴歸分析,其中預測變數
X 被認為是固定的。
Pearson 相關係數可能是最廣泛使用的相關度量。它要求變數
X 和 Y 是來自區間尺度(計算平均值和標準差有意義的尺度)的隨機變數。
無需其他假設即可獲得 r 值。然而,如果對關係進行推論(例如,我們設置了一個零假設,即
r = 0;無相關性),那麼Pearson相關係數假設
X 和 Y 的聯合分佈是“二元常態分佈”(三維鐘形曲線)。此外如果任一變數的變異量為零,則
r 未定義。雙變數常態性代表著 X 和
Y 都必須來自常態分佈,但反過來不一定成立。測試常態性是一個棘手的統計領域。
歷史背景
Sir Francis Galton爵士通常被認為是“發明了”迴歸方法。他是Charles
Darwin的堂兄。Galton開創了人類學(和優生學)統計學的先河。通過量測父親和兒子的身高,Galton觀察到高個子男人往往生出個子高大的兒子,但兒子與父親的平均水準(平均值)相差不遠。高爾頓將這種現象稱為“向平庸迴歸”,現在通常稱為“向平均值迴歸”。每當一個隨機變數被概念化為影響另一個變數時,就會採用“迴歸”術語。有點令人困惑的是,受到影響的變數有幾個名稱:因變數、結果變數、反應變數、解釋變數和迴歸變數。產生影響的一個或多個變數有許多名稱:自變數、預測變數、協變數、解釋變數和迴歸變數。
數學基礎
描述直線的方程式:
y = mx + c(1)(其中 m
和 c 是常數,x 和
y 是變數)。
對於
x 的每個值,我們都有一個精確的 y 值。x
和 y 之間的關係被認為是確定性的。但生物現象並非如此:x
和 y
之間的關係通常存在隨機性因素。例如如果我們從個體樣本中收集身高和體重的量測值,我們就可以根據體重預測人群中任何個體的身高。然而我們的預測會有一定程度的誤差。變數之間的這種固有隨機性被稱為概率或隨機關係。
統計推斷使用數值數據來解釋或預測一些現實世界的隨機現象。
數據與感興趣的現實世界現象之間的聯繫是一個統計模型。
所有統計模型中最簡單和應用最廣泛的一種是 LR。在進行
LR 的假設之前,將討論概率論的一些基本方面,這些方面為理解 LR
奠定了基礎。
隨機變數將數值結果反射到隨機過程。例如我們可以說擲六面骰子的結果是一個隨機變數 X,取值
1 到 6。注意可能需要為我們的現象賦值:我們可以說拋硬幣的結果是一個隨機變數
X,它分別取 0 或 1
的值來表示正面或反面。
隨機變數的期望值 E
是所有可能結果的加權平均值,其中權重是每個結果的概率。例如,六面擲骰子的期望值(也稱為期望值)是
1/6(1 + 2 + 3 + 4 + 5 + 6) = 3.5。
隨機變數的變異量(Var )描述了觀察值彼此不同的程度。它始終是一個非負數。變異量很小,表明大多數值接近平均值。變異量數學上被定義為
Var(X) = E([X − μ ]2)。這在代數上等於
E(X2) - (E[X])2。
將變異量概念化為數據中攜帶的資訊會很有用。
中心極限定理
(The central limit theorem, CLT) 指出,如果我們從任何具有有限變異量的分佈中反覆抽取“足夠大”的獨立觀測樣本,並且計算每個樣本的平均值,無論樣本來自的分佈形狀如何,平均值的頻率分佈近似於常態(Gauss)分佈。CLT
還暗示,隨著樣本量的增加,平均值的預期值等於真實總體平均值,其樣本變異量等於總體變異量除以樣本量
(n)。
LR
模型及其假設
LR 模型包括一個確定性或系統性分量,它對應於公式1,以及一個額外的隨機分量,它解釋了我們正在建模的現像中的固有隨機性:
Yi = b + b Xi + ei
(2)
Yi 指的是結果變數的第 i
種情況。其中 i 的範圍從 1
到 n(樣本量)。右側的確定性分量是β 0
+ β 1Xi,隨機分量是ε i。β 0和β 1是有興趣估計的參數(β
係數)。
這些估計通常由稱為普通最小平方法 (OLS) 的方法確定。
LR 可用於提供一個變數確實會影響另一個變數的證據,並在給定某些資訊的情況下對結果進行預測。
經典
LR 具有獲得“良好”OLS
估計所需的假設(稱為最佳線性無偏估計, best linear unbiased
estimators, BLUE)。支持 OLS 估計為BLUE的數學基礎對於數學背景有限的人來說可能具有挑戰性。儘管
OLS 估計為 BLUE, 所需的假設並不直觀,但它們也是模型設置的邏輯要求。
在
LR 中,與相關性不同。主要標準是我們有理由相信 X 影響
Y。儘管不是其數學模型的假設。
此外使用
LR 來解釋生物現象帶來了使用線性方程對相互關聯,和復雜機制進行建模的科學合理性問題。在考慮應用任何解釋模型(尤其是
LR)時,了解潛在過程及其可能的反應很重要。無論統計完整性如何,在沒有批判性思考的情況下將數據任意投入
LR 可能會產生令人困惑和誤導的結果。
模型設置
想像我們有一個由連續結果變數 Y 和單個預測變數 x(離散或連續)組成的數據集。現在將共變數表示為
x,而不是 X,以表明它被認為是固定的。只有一個預測變數的情況稱為簡單
LR。有兩個或更多預測變數的情況稱為多重 LR。在此將專注於簡單的
LR,但所有概念都可以外推到多重LR。如果我們因為隨機分量ε而繪製
Y 與 x 的關係圖,(根據方程式 2),我們將得到一個散點圖,而不是一條直線。LR要求直線。為了滿足這個需求,建立以下線性函數。
E (Y/ x) = b0 + b1x(3)
LHS 是給定相應 x 值的結果變數
Y 的預期值。此結構是LR的基礎。它可以被概念化為給定
x 值的 Y 的總體平均值。在 RHS
上,β 0 是截距(x
為 0 時 Y
的總體平均值)。β 1 是斜率,給出
x 單位變化的結果總體平均值的變化。
βi被認為在母群中具有實際的固定值:它們是常數,而不是隨機變數。
在這個模型中,假設“連續預測變數和結果變數是線性相關”(假設
1)。這是一個關鍵假設,可以通過散點圖上 y 和
x
之間的關係進行評估。建立數據的散點圖是數據分析中的一個重要步驟。請注意可以向右邊添加項,這些項目在共變數方面不是線性的;例如添加一個
x2 項(二次項),但參數(β
係數)必須是線性的。在多元迴歸分析中,預測變數被認為是線性相關的和可加的。分類和連續結果變數都可以使用迴歸技術,但對於
LR,我們假設“結果變數是連續的”(假設
2)。如果我們的共變數是分類的,例如控制組和治療組分別指定為 0 和
1,那麼 LR 分析在數學上等同於具有相等變異量的
t 檢驗。在這種情況下,線性假設沒有意義,也不是必需的。
在經典
LR 中,x
根本不被視為隨機,它被視為固定數據。共變數採用什麼分佈並不重要。我們假設“x
沒有隨機分量,包括沒有量測誤差”(假設 3)。這一點可能會令人困惑,特別是在共變數實際上是隨機變數的情況下。可以建立隨機迴歸模型,但我們在這裡不考慮。重要的是隨機分量的整體分配給誤差項,它與共變數無關。
另請注意,公式 2 中的誤差項未了方便在公式 3
中消失。從公式 2 到公式 3
的步驟是取公式 2 的兩邊的期望值。數學如下:
E (Y/ x) = E (b0/
x) + E ([b1x/ x) + E (e/ x)(4)
現在,β和
x 被視為常數,常數的期望值就是常數本身,因此我們可以將公式 4 改寫為:
E (Y/ x) = b0
+ b1 x + E (e /x)(5)
為了達到方程式 2 的方便的線性形式,必須假設
E( ε |x) = 0。這是零平均誤差的假設(以 x
為條件)。這是另一個關鍵假設'(假設 4)。
估計參數
方程3描述了我們現實世界現象的模型。這些參數在總體中具有實際值,但是未知。參數β 0
和β 1的ordinary
least squares (OLS)估計值通常分別表示為b0
和b1。
目的如果是通過數據建立一條“最佳配適線”。如果我們稱從配適線到觀察點的垂直距離為“殘差”(如果高於該線則為正,如果低於該線則為負)。那麼可以通過最小化平方和來建立最佳配適線的殘差。計算b0和b1比較簡單,滿足這個要求(一般是用統計完成的)。
關於數據中資訊的假設
在建立最佳配適線時,我們假設每個數據點“值得”相同數量的資訊。如果某些數據的價值低於其他數據,那麼我們的迴歸斜率將被資訊豐富的數據所吸引,而被資訊貧乏的數據所排斥。變異量
( σ 2 )
可以被概念化為資訊的倒數。如果我們的數據點都靠近迴歸線,那麼變異量就很小。如果迴歸線的垂直分佈大,則變異量大。
假設每個數據點對總資訊的貢獻相等,因此具有相同的變異量σ 2 。因為我們數據的垂直分佈是對誤差的估計值,所以我們假設誤差具有恆定變異量σ 2 。這是恆定變異量的假設,稱為“同變異量性”(假設
5)。其推論是如果所有數據點都承載相同的資訊負載。我們還假設數據點不相關,即我們有來自基礎總體的獨立觀察。這相當於“不相關的錯誤”(假設
6)。這代表著一個數據點不能影響另一個數據點。
檢查假設
有多種方法可以評估模型的所謂“配適優度”。該術語是指模型實際滿足假設的程度。這包括目視檢查數據和殘差。
許多統計檢驗也可用於評估配適優良程度,例如 R 2值,它描述了由預測變數解釋的結果變數的變化量。然而殘差檢查是LR
模型檢查的最重要技術,應該對所有 LR 分析進行。
在測試
LR 的假設時,記住現實世界現象的隨機分量,在LR
模型中的誤差項被捕獲在概念上很有用。這代表著希望看到殘差中的隨機性(代表誤差)。這可以通過根據預測值直觀地評估散點圖中的殘差值評估。非隨機模式表示存在問題。
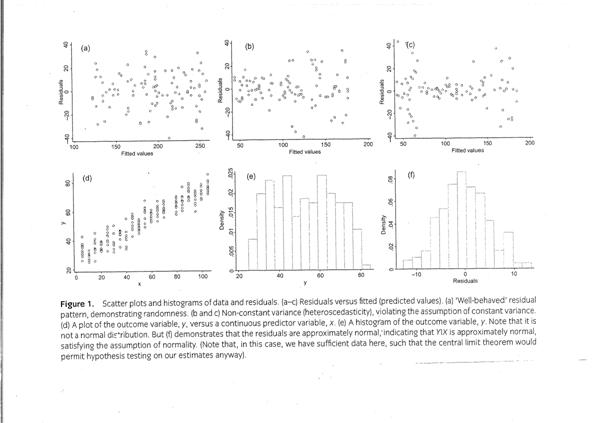
圖 1.
數據和殘差的散點圖和直方圖。(a-c)殘差與配適(預測值)。
(a) “良好”的殘差模式,顯示隨機性。
(b 和 c) 非恆定變異量(異值變異量),違反了恆定變異量的假設。(d)
結果變量 y 與連續預測變量 x
的關係圖。 (e) 結果變量 y
的直方圖。 請注意它是不是常態分佈。但是 (f) 表明殘差近似常態,表明
Y|X 近似常態,滿足常態性假設。(請注意,在這種情況下這裡要有足夠的數據,因此中心極限定理將允許對我們的估計進行假設檢驗)。
對於
LR 的應用,建立殘差與預測值的散點圖是診斷過程中一個簡單而有效的步驟(圖 1a)。可以通過將結果變數與預測變數作圖來檢查。
假設
1(線性):模式應該近似線性。曲線模式表明線性模型可能不是最佳配適,可能需要添加更複雜的模型(例如二次項)。
假設
2(結果變數(Yi)是連續的):數據可以取一定範圍內的任何值(僅受量測準確度的限制)。
假設
3:如果共變數與誤差項相關,則違反假設 3。如果存在較大的量測誤差或存在與包含的共變數相關的重要遺漏變數,則可能會發生這種情況。已經開發了各種迴歸技術,試圖解釋共變數中的量測誤差,以及不清楚是
X 影響 Y 還是 Y
影響 X 的情況。這些被稱為模型迴歸 II。在此不討論這裡確定的經典
LR 模型。
假設
4(零條件平均誤差)實際上是一種形式化線性假設的方法,可以通過殘差與預測值的散點圖進行評估。殘差應隨機散佈在零線周圍,沒有清晰的分佈模式。
假設
5(誤差的恆定變異量)也可以通過殘差與預測值的散點圖進行評估。隨機分佈表明變異量是恆定的。如果分佈變化,則違反恆定變異量的假設(圖
1b 和 c)。
假設
6(誤差不相關)要求每個觀測不提供關於另一個觀測誤差的資訊。這相當於Y
值以 x
值不相關為條件,並且與恆定變異量的假設密切相關。如果錯誤沒有攜帶相同的資訊,那麼它們應該被適當地加權以獲得最佳配適線。
為了避免相關性,我們應該確信結果變數觀察是獨立的。如果沒有我們必須使用可以處理數據相關性的方法。這涉及其他迴歸方法,例如參數估計的廣義估計方程方法或混合線性模型。
常態假設
如果我們滿足所有假設,我們將對β參數進行“良好”的估計。但是如果我們現在想要執行統計假設檢驗,我們需要有一個檢驗統計量,其中包含我們的參數估計資訊並且來自可管理的概率分佈,通常是常態分佈或相關的學生
t 分佈。
現在可以通過兩種途徑實現這一目標。首先可以通過堅持 Y|x 來自具有平均值
E(Y|x) 和變異量σ 2的常態分佈來“整理”我們的假設。這就是“正常假設”(假設
7)。這等效於來自平均值為 0 且變異量為σ 2的常態分佈的誤差(以
x 為條件)。在數學簡寫中,這寫為ε |x ∼ N(0, σ 2 )。這個數學公式包含了
LR 的大部分假設。
殘差代表理想化的誤差,我們通過確定殘差是否具有常態分佈,來檢查常態性假設。
在
x 是分類的情況下,給定 x 的誤差必須來自常態分佈。
因此,在
x 代表控制組和處理組的情況下(相當於變異量相等的 t
檢驗),我們要求來自兩個組的數據都來自常態分佈。我們使用直方圖和殘差與預測值的散點圖來評估殘差。請注意結果變數或共變數不一定必須服從常態分佈。如果誤差(以
x 為條件)來自平均值為零的常態分佈,並且常數變異量σ 2 ,那麼即使具有小的數據樣本,我們的係數估計值,保證還具有常態分佈,並且將在統計假設檢驗(圖1D-F)可以表現良好。當
xi實際上來自連續隨機變數 X 時,殘差的分佈近似於給定
X 時 Y 的分佈。
其次即使錯誤不是來自常態分佈,CLT 也可以讓我們滿足常態性假設。如果我們有一個“足夠大的樣本”,那麼由於
CLT,估計值將來自近似常態分佈。CLT 對“數據足夠大”的問題保持沉默。大於
50 的樣本量將足以不計較常態性假設。
如果殘差似乎不具有常態分佈,則廣泛採用的技術是轉換數據。一種通常對右偏數據有用的常用方法是對於結果變數(yi)的對數化並重新運行模型。如果數據轉換沒有產生常態化,而且如果樣本太小而無法支持
CLT,那麼最好的選擇可能是使用非參數技術。
各種常態性檢驗很容易地使用統計軟體檢測,例如 Shapiro-Wilk
檢驗。然而它們可能不能檢測小樣本的非常態性。相反,於大樣本,這些檢驗可能表明非常態性,而實際上數據是正常的常態。應該通過檢查直方圖和
QQ 圖以及對 5 到 50
之間的樣本大小進行Shapiro-Wilk檢驗,來合理的嘗試檢驗常態性假設。
處理異常值
最初的探索性數據分析應該包括箱線圖和散點圖(box plots and scatter plots),很可能已經確定了數據集中的異常值(Outliers)。異常值本身並不違反
LR 假設,但它們可以產生不能反映現實的估計。在小樣本中,單個異常值可能會“偏離”出最佳配適線。有多種統計技術可用於檢測異常值,包括評估Cook’s
distance。然而,如何處理它們在很大程度上是主觀的。我們建議除非有正當理由相信它們代表錯誤數據,否則應將它們包括在內。或者可以在有或沒有異常值的情況下呈現結果。
多重迴歸
儘管我們專注於簡單的 LR,但這些假設可以應用於我們有多個預測變數的常見情況。必須特別注意這些模型。作為一般規則,研究人員應該瞄準最簡約的模型,即與Occam’s
razor(Entities
should not be multiplied unnecessarily)相一致的模型。進一步的假設是共變數不共享資訊,即它們是線性無關,沒有多重共線性(multicollinear)。
多重共線性將導致我們估計的標準誤差增加。此外已發表文獻中的多元迴歸經常遇到“過度配適”的問題。這是指我們的模型中的共變數多於我們的樣本量。作為粗略的經驗法則,每個共變數應該至少有
10 個數據點。評估多重 LR 的假設與簡單
LR 使用相同的技術,尤其是殘差圖的評估。此外對部分殘差圖的評估有助於發現非線性。
模型驗證
一旦我們有了
LR 模型,就可以放知道它可以做出準確的預測。統計學家使用多種技術來評估模型的內部和外部有效性。
在疾病的預測模型中,校正是指模型估計的特定時間段內發生疾病的概率,與同一時期結果的實際頻率,兩者之間的一致性。 辨別力(Discrimination)是指模型區分那些發展或不發展感興趣的條件的能力。13
數據拆分和引導是評估模型內部有效性的方法。數據分拆(Data splitting)涉及以樣本的一部分來建立模型,其餘部分來測試其預測能力。Bootstrapping
是一種從整個數據集中進行替換採樣並使用模擬數據來測試預測的技術。
結論
在此已經討論了 LR
在統計建模中使用的假設,並指定了研究採取的關鍵步驟,以確保所使用的模型適用於被詢問的數據。我們建議所有研究在其統計方法的討論中提供一個聲明,表明
LR 的假設已經得到滿足。 |