中興大學 生物系統工程研究室 陳加忠

資料來源:

Korean J Anesthesiol 2019 December 72(6): 558-569

https://doi.org/10.4097/kja.19087

Jong Hae Kim

Department of Anesthesiology and Pain Medicine, School of Medicine, Daegu Catholic University, Daegu, Korea

摘要

多重重合性表示多元迴歸模型中解釋變數之間的高度線性相關性，並且會導致錯誤的迴歸分析結果。多重重合性的診斷工具包括變異數膨脹因子（VIF），條件指數和條件係數以及變異數分解比例（VDP）。多重重合性可以通過多重迴歸模型的確定係數（R_h²）表示，其中一個解釋變數（Xh）作為模型的反應變數，而其他解釋變數（X_i [ i ≠h]）作為其解釋變數。變異數（σ_h²）構成最終迴歸模型的迴歸係數的平方與VIF（1/(1–R_h²）)成正比。因此，增加了在R_h 2（強多重）增加σh²越大σH² 的結果產生不可靠的概率值和迴歸係數的信賴區間。來自標準化解釋變數的相關矩陣的最大特徵值與每個特徵值之比的平方根稱為條件指數。條件號碼是最大條件指數。當VIF大於5到10或條件指數大於10到30時，存在多重重合性。但是它們不能表示多重重合性的解釋變數。從所獲得的VDPs特徵向量可以通過顯示出的膨脹程度根據各條件指數以識別複共變數σ_H²。當對應於高於10到30的共同條件指數的兩個，或更多VDP大於0.8到0.9時，它們的相關解釋變數是多重重合性的。排除多重重合性解釋變數會導致統計更穩定的多元迴歸模型。

介紹

一項前瞻性隨機對照試驗評估了單個解釋變數對其主要結局變數的影響，而其他解釋變數的未知影響則通過隨機化最小化[1]。但是在觀察性研究或回顧性研究中，在收集數據之前不進行隨機化，並且存在除目標變數以外的其他解釋變數的混淆作用。為了控制對單個反應變數的混淆影響，使用了多變數迴歸分析。但是在大多數情況下，解釋變數是相互關聯的，並且會彼此產生重大影響。解釋變數之間的這種關係，損害了多變數迴歸分析的結果。解釋變數之間的相互關係稱為“多重重合性”。在這篇論述中，定義多重重合性，以各種措施來檢測它，並且其上的影響多重線性迴歸分析的結果進行說明。在附錄中，盡可能詳細地描述了多重重合性的概念及其檢測方法，以及其數學方程式，以幫助不熟悉統計數學的讀者。

多重重合性

精確的重合性是兩個解釋變數X₁和X₂之間的理想線性關係。換言之，精確的重合性（例如，如果一個變數決定了另一個變數發生，如X₁ = 100-2X₂）。如果存在這樣的關係兩個解釋變數（例如，X₁ = 100-2X₂ +3X₃ ）則定義為多重重合性。在多重重合性下，一個以上的解釋變數由其他變數確定。

但是重合性或多重重合性不需要確定它們的存在是精確。牢固的關係足以具有顯著的重合性或多重重合性。確定係數是由建立在一個或多個解釋變數上的迴歸模型預測的反應變數中變異數的比例。但是，反應和解釋變數分別是一個解釋變數和其餘變數的多元線性迴歸模型的確定係數（R_i²）也可以用於測量解釋變數之間的多重重合性程度。R_i² = 0表示解釋變數之間不存在多重重合性，而R_i²= 1表示變數之間存在精確的多重重合性。從具有精確多重重合性的變數中刪除一個或多個解釋變數不會導致多元線性迴歸模型的資訊丟失。

變異數膨脹因子

迴歸係數的變異數與（1/(1–R_h²）)成正比，稱為變異數膨脹因子。考慮到的R_h²範圍² （0 ≤R² ≤ 1），R_h² = 0（完全不存在多重重合性的）的迴歸係數的變異數最小化的興趣，而R_h² = 1（完全多重）使得該圖變異數無窮大（ 圖1）。變異數膨脹因子（1-R_h²）的倒數稱為公差。如果變異數膨脹因子和公差分別大於5到10和小於0.1到0.2（R² = 0.8到0.9），則存在多重重合性。

儘管變異數膨脹因子有助於確定多重重合性的存在，但它無法檢測到導致多重重合性的解釋變數。

如前所述，強大多重重合性增加了迴歸係數的變異數。變異數的增加也增加了迴歸係數的標準誤差（因為標準誤差是變異數的平方根）。標準誤差的增加導致迴歸係數的信賴區間擴大到95％。誇大的變異數還導致確定檢定迴歸係數是否為0的t統計量減小。在t統計量較低的情況下，迴歸係數不重要。較大的信賴區間和無關緊要的迴歸係數使最終的預測迴歸模型不可靠。

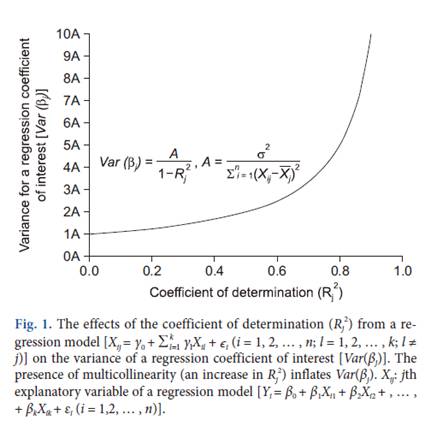
圖1.迴歸的確定係數（R_j²）的影響

Fig. 1. The effects of the coefficient of determination (Rj²) from a regression

model [Xij = γ0 + kl 1 =Σ γlXil + ϵi (i = 1, 2, … , n; l = 1, 2, … , k; l ≠

j)] on the variance of a regression coefficient of interest [Var(β_j)]. Thepresence of multicollinearity (an increase in Rj²) inflates Var(βj). Xij: jthexplanatory variable of a regression model [Yi = β₀ + β₁X_i1 + β₂X_i2 + , … ,+ β_kX_ik + εi (i = 1,2, … , n)].

條件號碼和條件指數

使用由標準化解釋變數組成的矩陣，從計算中獲得的特徵值（λ）可用於診斷多重重合性。特徵值的總和等於解釋變數的數量。平均特徵值是1。因為總和特徵值是恆定的，它們的高的最大的存在值，表示其它特徵值是相對低的最大值（λ_max）。特徵值接近0表示存在多重重合性，其中解釋變數高度相關，即使數據中的很小變化也會導致迴歸係數估計值出現較大變化。最大值與每個特徵值（λ₁ ，λ₂ ，… ，λ_k ）之比的平方根稱為條件指數：

最大的條件指數稱為條件號碼。在10到30之間的條件係數表示存在多重重合性，並且當值大於30時，多重重合性被認為是強重合性。

變異數分解比例

從特徵值派生的特徵向量用於計算變異數分解比例，該變異數分解比例通過多重重合性，表示變異數膨脹的程度，並能夠確定涉及多重重合性的變數。每個解釋變數具有與每個條件指標相對應的變異數分解比例。一個解釋變數的變異數分解比例的總和為1。如果對應於高於10到30的條件指數，再其兩個或更多變異數分解比例超過80％至90％，則可確定在對應的解釋變數之間存在多重重合性超過變異數分解比例。

處理多重重合性的策略

數據的錯誤記錄或編碼可能會無意間導致多重重合性。例如在迴歸分析中無意中重複包含相同變數會產生多重合性迴歸模型。因此防止數據處理中的人為錯誤非常重要。從理論上講增加樣本量會減少迴歸係數的標準誤差，因此會降低多重重合性度[2]。

但是在強多重重合性下，標準誤差並不能總是減少。舊的解釋變數可以使用新收集的變數代替，後者可以更準確地預測反應變數。但是將新病例或解釋性變數包括在已經完成的研究中，需要大量的額外時間和成本，或者在技術上根本不可能。

將多重重合性變數組合成一個可以是另一種選擇。屬於共同類別的變數通常是multicolinear。因此將每個變數組合成更高的層次變數可以減少多重重合性。另外具有近似精確重合性的變數之一可以由方程式與另一個變數來表示。將方程式包含在多元迴歸模型中可刪除共線變數之一。主成分分析或因子分析還可以生成以單個變數結合了多重重合性變數的。但是使用此過程無法評估各個多重重合性變數的影響。

最後可以藉由變異數分解比例確定的多重合性變數，自迴歸模型中刪除，使其在統計上更加穩定。但是僅原則上排除多重合性變數，並不能保證其餘相關變數的存在，應在多變數迴歸分析中研究其對反應變數的影響。排除相關變數會產生有偏差的迴歸係數，從而導致比多重重合性更嚴重的問題。嶺((Ridge)迴歸是在迴歸模型中包含所有多重合性變數的一種替代方式[3]。

數值範例

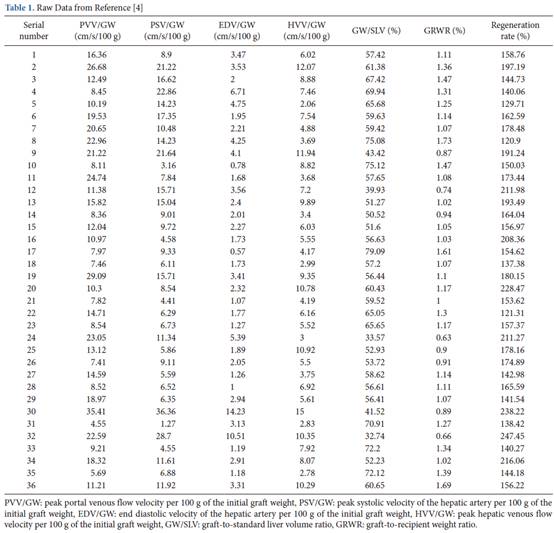
在本節中，使用先前發表的論文[4]的數據（表1），根據變異數膨脹因子，條件係數，條件指數和變異數分解比例評估其多重重合性。考慮的反應變數是活體供體肝移植（LDLT）兩週後的肝再生率。在所考慮的六個解釋變數中，有四個是移植後一天測得的肝血流動力學參數，包括肝動脈的峰值門靜脈血流速度（PVV），峰值收縮速度（PSV）和舒張末期速度（EDV），以及肝靜脈峰值流速（HVV）。通過將這些參數除以初始移植物體重量（GW）的100克來標準化。考慮的其他解釋性變數是移植物與收件人的重量比（GRWR）和GW與標準肝體積比（GW / SLV）。

由於從門靜脈和肝動脈流入部分肝移植物所產生的切應力是肝臟再生的驅動力[5]，因此可以假定標準化的PPV，PSV和EDV（PVV / GW，PSV / GW和EDV / GW分別與肝再生速率呈正相關。標準化HVV（HVV / GW）與肝臟再生速率之間也存在正相關關係。因為流入量構成了從肝移植物通過肝靜脈的流出量。另外肝移植物越小，剪切應力越高。因此相對於受體重量和標準肝體積的移植物重量預期與肝再生速率負相關。

在上述論文中發現了每個解釋變數與肝臟再生率之間的預期單變數相關性[4]。肝之間顯著相關動態參數（PVV / GW，PSV / GW，EDV / GW和HVV / GW）和相對接枝權重（GRWR和GW /之間SLV），因為它們共享共同的特性的預期。

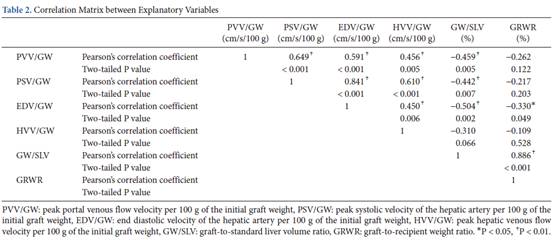
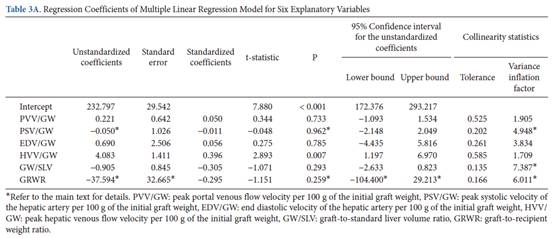
因此將所有這些解釋變數，用於多元線性迴歸分析可能會導致多重重合性。正如預期的那樣，解釋變數的相關矩陣顯示出變數之間的顯著相關性（表2）。基於使用六個解釋變數（表3A）通過多元線性迴歸分析計算出的迴歸係數，獲得了以下迴歸模型。

肝再生率= 232.797 + 0.221×PPV⁄GW-0.050×PSV⁄GW + 0.690×EDV/GW + 4.083×HVV/GW−0.905×GW/SLV-37.594×GRWR（R² = 0.682，P <0.001）

雖然PSV / GW的增加會導致肝臟再生率的增加，但根據簡單線性迴歸分析的結果[4]，PSV / GW的單位增加會降低0.05％，儘管這並不重要。在另外雖然在所述GRWR一個單位的變化的影響的再生速率是最強的（在37.954％的減少每單位增加再生率），其迴歸係數不是其充脹變異數，統計學顯著是由於其通向的32.665高標準誤差和寬的95％信賴之間間隔-104.4和29.213。這些不可靠的結果是由多重重合性產生的。多重重合性由GW /SLV，GRWR和PSV/GW（大於或非常接近5）的迴歸係數的高變異數膨脹因子表示，分別為7.384、6.011和4.948。它們在表3A中用星號表示。大於10的三個條件指數（表3B中的記號）還表明，由於多重重合性而產生了三個線性相關性。但是他們無法識別具有多重重合性的解釋變數。

在表3B中用星號表示超過0.8的變異數分解比例。對應於最高條件指數（條件號碼）（即0.99和0.84）的那些變數表明，迴歸模型的最主要線性依賴性由GW / SLV和SLV迴歸係數的變異數膨脹的99％和84％解釋。GRWR。兩個解釋性之間的強線性相關變數也由最高Pearson’s相關係數發現（R = 0.886）（表2）。但是可以在表2中找到PSV / GW和EDV / GW之間的第二個最強相關性（R = 0.841），似乎並沒有在多元線性迴歸模型中引起多元重合性。

儘管PSV / GW的變異數膨脹因子（4.948）低於5，但非常接近。另外它們的變異數分解比例中只有一個對應於條件指數11.938，超過0.8。但是根據Liao等[6]，如果將用於多重合性診斷的變異數分解比例的臨界值設置為0.3，，兩個解釋變數是多重重合性的。因此有理由從迴歸模型中排除GW / SLV，但尚不清楚是否從迴歸模型中刪除了PSV / GW。

排除GW / SLV和PSV / GW產生了穩定的迴歸模型（表4A），

肝再生率= 209.393 + 0.392×PVV/GW + 1.006×EDV/GW + 4.410×HVV/GW−68.832×GRWR（R² = 0.669，P <0.001）

所有變異數膨脹因子均小於2。特別是GRWR迴歸係數的變異數膨脹因子從6.011降低至1.137，其標準誤差從32.665降低至14.014，95％信賴區間從（-104.4，29.213）至（-97.413，-40.251）。 

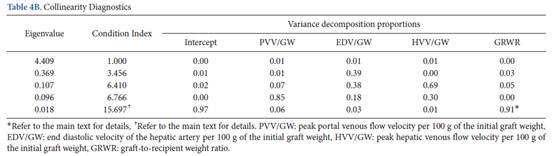
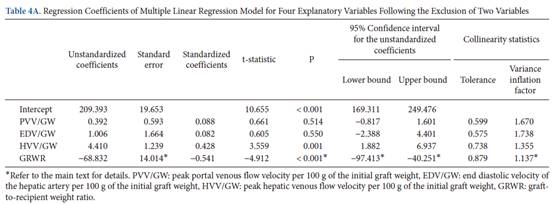根據上述變化，迴歸係數的概率值變得小於0.05（從0.259到< 0.001）。儘管條件係數仍大於10，但僅存在一個大於0.9的變異數分解比例（表4B）。需要注意的是，截距項對該分析並不重要。測定係數（R²）從0.682到0.669的微小變化表明資訊損失可忽略不計。

結論

多重重合性扭曲多元線性迴歸分析獲得的結果。由於多重重合性而導致的迴歸係數變異數的膨脹，使得該係數在統計上不顯著，並擴大了它們的信賴區間。如果變異數膨脹因子和條件係數分別大於5到10和10到30，則確定存在多重重合性。但是他們無法檢測到哪些解釋變數是多重重合性的。為了確定具有多重重合性的變數，使用了變異數分解比例。如果變異數分解比例大於0.8到0.9，對應於條件指數大於10到30，則與對應於公共條件指標的變異數分解比例相關的解釋變數是多重重合性的。總之多重合性的診斷和多重合性解釋變數的排除使得能夠建立可靠的多元線性迴歸模型。