|
資料來源:
Steponas RAUDONIUS
Aleksandras Stulginskis University
Studentų
11, Akademija, Kaunas distr., Lithuania
E-mail: steponas.raudonius@asu.lt
ISSN 1392-3196 / e-ISSN 2335-8947
Zemdirbyste-Agriculture, vol. 104, No. 4 (2017), p. 377‒382
DOI 10.13080/z-a.2017.104.048
摘要
實驗統計的適當正確應用是植物和作物研究中非常重要的問題。對農業和生物學期刊上發表的研究論文的調查結果表明,作者經常錯誤地使用或解釋統計數據。在調查的各個階段,研究人員通常沒有足夠的重視統計的正確應用。本文的目的是強調植物和作物研究中廣泛使用的統計方法的要點。本文包括研究設計和統計分析、基本假設和轉換、ANOVA
應用、迴歸和相關分析、研究結果展示等主題。在作物研究的各個階段提供了正確使用統計方法的建議。本文不涵蓋超出傳統
ANOVA 和迴歸的統計方法。這些需要更先進的電腦軟體來執行它們。
介紹
統計方法的應用可以幫助研究人員完成所有階段的研究:從計劃到撰寫出版物。但我們應該記住,如果調查設計不當,統計數據將無濟於事。另一方面,統計方法的不當應用會導致錯誤的結論。調查結果和結論的很大程度上取決於實驗設計,和對其結果的統計分析兩者如何相互對應(Rudolph
et al., 2016)。
科學家和專業統計學家一起工作的研究中心,通常可以實施更好的調查計劃、實驗和報告品質(Fenkon,
1995 )。但在大多數情況下,研究人員只是根據他們的知識和理解以使用統計方法。對生物和農業期刊的調查表明,至上世紀末,在多達70%的研究論文中,作者錯誤使用以解釋統計數據(Johnson,
Berger, 1982)。我們期待現在的情況會好一些。然而查看了在2013-2017年期間對一些農業期刊的研究稿件的評論,發現55%的稿件需要對於其統計分析結果的使用和解釋進行改進。Kramer
等提出了類似的結果(2016)。他們檢查了《美國園藝科學學會雜誌》(JASHS)某些出版物。幾乎一半的審查文章在實驗統計應用方面存在問題。其他研究領域的論文中也出現了在實驗計劃和統計方法應用方面的錯誤。例如對英國和美國發表的動物研究數據的論文報告其調查結果表明,只有
59% 的研究陳述了假設或目的,87% 的研究沒有使用隨機化;只有
70% 的出版物報導有關於誤差或可變性量測的資訊(Kilkenny et al., 2009)。
通常在調查的計劃階段就已經出現了一些錯誤。很多時候,應用統計方法與實驗設計不相符。在某些情況下,作者過分關注於統計方法的應用,而忘記解釋研究結果的生物學意義。關於如何進行統計分析的資訊往往不足。本文的目的是強調在植物和作物研究中廣泛使用的統計方法的要點,並針對調查的各個階段,對於正確使用統計方法提出建議。
研究設計和統計分析
為各種調查工作制定適當的設計非常重要:包括田野、溫室、實驗室和觀察性研究。開始時應明確定義實驗單元。實驗單位是應用處理的最小單位(Federer,
Crossa, 2005)。例如田間試驗地區塊、溫室試驗盆器、實驗室試驗的培養皿或要進行遺傳調查取樣的單株植物。通常實驗單位大於觀察或量測單位。選擇的實驗單元應該能夠進行適當的處理,並且處理應該能夠用以驗證假設。
通常處理在空間和時間上重複。區分真重複和偽重複非常重要。當處理應用於幾個獨立的實驗單元時,會發生真正的複製。當從同一個樣本中進行多次量測(子抽樣)時,我們沒有真正複製的情況。例如:從一盆中分別量測經過除草劑處理的植物。從田間試驗區組成一個土壤樣本,並重複四次相同的化學分析。在這種情況下,處理僅應用於一個實驗單元,這裡沒有真正的複製。研究人員也不應該為實驗室實驗計劃錯誤地的重複(Morrison
& Morris, 2000; Onofri et al., 2010)。在某些情況下,可以在沒有真正重複的情況下進行調查,但不能應用傳統的統計方法
ANOVA 或迴歸和相關性。然後應該使用其他適當的統計方法進行數據評估,例如信賴區間(CI)檢定,t檢定,基本統計指標:包括標準差(Standard
deviation, SD),標準偏差(Standard error ,SE)和變異係數(CV)。
研究結果的精確度和結論的品質很大程度上取決於重複次數。在重複次數和標準偏差之間建立了顯著的關係。
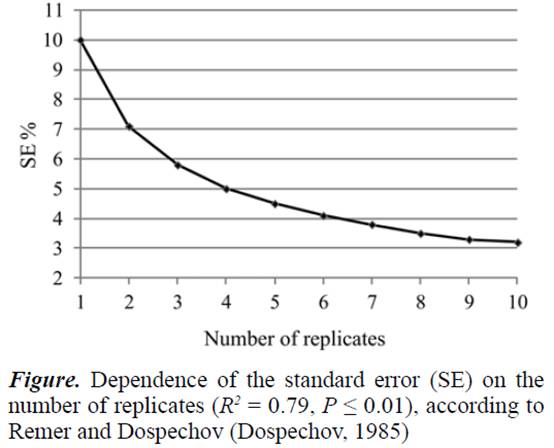
圖:數字。根據 Remer 和
Dospechov (Dospechov, 1985),標準偏差 (SE)
對重複次數的依賴性 (R2 = 0.79, P
≤
0.01)
對於農藝實驗,4-6 次重複通常是最佳數量,但在某些情況下,最多需要
8 次重複。例如當實驗在小區塊上進行時,處理數月很少,處理之間的差異很小。實驗統計的應用可以幫助選擇適當的重複次數。公式
1 可用於計算適當的重複次數:n=2t2s2/d2
 (1) (1)
其中
t 是 t 表中根據機率水準和誤差(殘差)自由度得出的值,S2
– 變異數(來自類似實驗數據的實際值)和 d –
兩種處理之間的預期差異。
因為可以通過t檢定來檢定兩種處理之間差異的顯著性:
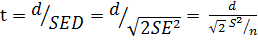 (2) (2)
其中
t 是計算的 t 值,SED –
差異標準偏差和 SE – 標準偏差。計算所需的重複次數也可以基於最小顯著差異
(LSD):
 (3) (3)
兩種處理之間的預期顯著差異不應小於指定顯著性水準的 LSD:
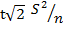 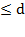
在指定的顯著性水準上小於 LSD:
為了正確使用實驗統計方法,必要在各種實驗的設計中應用隨機化。隨機化是在實驗單元上隨機分配處理或實驗材料,以獲得獨立誤差的客觀方法。
研究計劃的另一方面的重要性是應用適當的抽樣。特別是在每個實驗單元中選擇正確的抽樣規模。抽樣數據的平均值應對應該在於所需準確度水準的總體平均值。為此我們才可以使用統計數據。
我們可以通過幾種方式獲得初始數據:1)以前在類似條件下,進行的類似實驗數據,2)在類似條件下正在進行的類似實驗數據,以及
3)為確定抽樣規模而專門規劃的抽樣。在確定某個變數的樣本大小之前,值得分析在類似條件下以類似實驗得到的數據。
我們應該找出處理之間顯著差異大小,以及使用的樣本大小。如果我們計劃獲得相似的差異,我們可以使用相同的樣本規模。但是如果我們期望較小的差異,我們必須增加樣本規模。
計劃的抽樣規模可以在正在進行的實驗中進行修正。一開始,我們只對兩種處理的實驗單元進行抽樣,我們預計它們之間存在顯著差異。我們立即對於初始數據
t 或 CI
檢定進行統計分析。如果我們證明使用計劃抽樣規模選擇的兩種處理之間存在顯著差異,我們可以延長對所有實驗單元的抽樣。如果我們不能拒絕虛無假設,我們必須增加抽樣規模。
有時,所調查指標的可變異水準(variability level)是未知的。在這種情況下,值得進行初步抽樣和計算統計指標(例如,CV、SD
或 SE),以用於不同的樣本大小。
基本假設和轉換
只有滿足基本假設的結果應用傳統統計,才能得出可靠的結論。至少應滿足三個關鍵假設:常態性、變異數同質性和實驗誤差的獨立性。
常態性假設表明如果常態分佈是錯誤。這代表著偏差也來自常態分佈。實驗數據的偏差或殘差圖表有助於評估統計方法,研究人員應檢查複制區塊之間的數據差異有多大。當存在實質性差異時,可能無法滿足常態性假設(Hoshmand,
2006)。每株或每葉片的害蟲數據、雜草密度數據、計數數據或百分比分數通常不是常態分佈的。常態性假設可以通過以下方式實現:1)增加實驗單元內的抽樣規模,以及
2)應用數據轉換。
同質性假設代表著處理的變異數應該是相似的。在許多情況下,處理平均值之間的變異性差異並不大,這一假設得到滿足,並且使用變異數分析或迴歸分析是正確。
當處理平均值之間出現較大差異時,處理之間的變異數通常非常不同,並且違反了同質性假設。當研究人員在實驗中加入未經處理的對照組時,通常會發生這種情況。可以通過以下方式滿足同質性假設:
1) 根據變異性,將分組處理為同質組,
2) 從處理的 ANOVA
程序中排除其平均值與其他顯著不同的數據。該平均值與其他處理平均值顯著不同,而且沒有正式的統計分析。
3) 應用數據轉換。
獨立誤差假設代表著一個觀察的誤差與另一個觀察的誤差並不相關。例如如果研究人員對距離很近的實驗單元應用相同的處理,則它們的結果將比位於更遠距離的單元,其結果更相似。當觀察被分組時,可能會缺乏獨立性,例如在偽複製、重複量測、子抽樣的情況下(Onofri
et al., 2010)。可以通過適當的隨機化、僅使用真實重複數據(子次抽樣數據的平均值)以及對重複量測或二次抽樣數據應用裂區設計來滿足獨立誤差的假設。隨時間重複量測的數據或子採樣數據可以作為子區塊數據進行統計評估(Onofri
et al, 2010)。例如,如果我們使用 5
次重複研究三種生長調節劑的作用,並且每個季節量測冬小麥莖的高度 4
次,則可以通過以下方式應用用於統計分析的裂區設計:主區塊 = 生長調節劑的應用,量測時間=
子區塊。
為了滿足假設,在計劃和進行實驗期間應採取適當的行動。如果出現與常態性和同質性的較大偏差,則應進行數據轉換。通常可應用對數、平方根和反正弦變換。
對數轉換:如果有證據表明平均值和標準差之間存在關係並且違反了同質性假設或數據顯示分佈偏斜,則建議進行對數變換。原始數據在統計分析之前轉換為
log10x。應該記住,這種轉換方式不適用於負值和零值。在這種情況下,應該應用 log (x
+ c),其中 c 是常數,等於 0.5
或 1。如果數據中存在大量零值,則應應用另一種轉換方式(Hoshmand,
2006 )。
平方根轉換:對非負值應用平方根變換 x' = √x。當每種處理的平均值和變異數成正比或數據偏斜明顯時,這種類型的轉換是合適。如果很多值都很小,特別是存在一些零值,最好使用變換
x' = √x + 0.5 或 x' = √x + 1。
平方根變換不如對數變換有效。在某些情況下,對數變換對偏度或變異數異質性過度校正。因而平方根變換是適用的。
當數據屬於百分比或比例且違反常態假設時,反正弦變換 x' = arcsin√x
是最合適的。通常,當百分比範圍大於 40% 時,建議進行此型轉換。如果數據值在
30% 到 70% 之間,則不建議進行轉換。有時,接近
0% 和 100% 的值的變化值遠低於
50% 左右的數值。在這種情況下,反正弦變換也是合適。
當應用迴歸模型時,有必要對模型的兩邊(反應和預測)進行轉換。研究人員應該確信數據轉換確實需要,並且實際上有效地滿足基本假設(Onofri
et al., 2010)。更多關於數據轉換的建議可以在 Hoshmand (2006)、Palaniswamy
和 Palaniswamy (2006) 以及
Welham et al.(2015)。
變異數分析應用
ANOVA
廣泛用於統計評估實驗數據。該方法特別適用於具有定性解釋變數(處理)的實驗數據。研究人員應該負責任地選擇
ANOVA 模型以獲得可靠的調查結論。模型選擇取決於實驗的類型,和研究的目標或假設。
單因子實驗
完全隨機設計
(CRD) 和隨機完全區組設計 (RCBD)
常用於單因子實驗。,因為變異的來源並不相同,研究人員應牢記實驗是如何計劃的以及使用什麼模型(表 1)。在
CRD
的情況下,複製的變異數不存在。拉丁方設計和不完全區塊設計在植物研究中很少使用。如果我們應用這樣的設計,我們應該使用足夠的變異數分析模型。
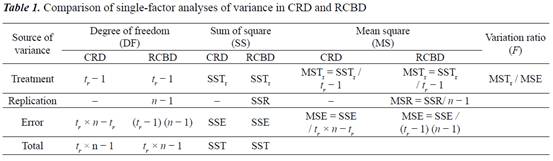
表 1 CRD 和 RCBD
單因子變異數分析比較
雙因子實驗
隨機完全區組設計和裂區設計在二因素實驗中更為常見。研究人員應該了解,使用這兩種設計的變異來源是不同的(表
2)。當使用裂區設計時,數據變化取決於應用了哪種類型的區塊(主區塊或副區塊)處理。應計算兩個不同的誤差(主區塊和子區塊)。因此,與使用
RCBD 時相比,裂區的其他 ANOVA 指標和檢定結果會有所不同。
在方法部分,應指出在主地區塊上研究了哪些因素處理,在子地區塊上研究了哪些因素處理。如果我們進行三個或更多因素的實驗,則有必要根據實驗設計使用適當的ANOVA模型
進行數據評估。

表
2. 隨機完全區組設計 (RCBD) 和
spit-plot 設計中變異數二因素分析的比較
研究人員應該探索解釋多因素實驗數據的因素相互作用結果。如果交互作用不顯著,則應檢查主效應。在這種情況下,因子實驗等同於單因子實驗。當相互作用建立時,研究人員應該檢查簡單的影響(例如,a1b0
- a0b0)並評估相互作用的特徵。在這種情況下,所檢查因素的主要效應不應呈現和討論(Hoshmand,
2006)。
變異數分析測試
ANOVA 結果用於測試處理平均值之間的差異。當應用
ANOVA 時,可以使用兩種類型的處理平均值比較:1)
配對比較包括處理平均值與對照的比較(計劃比較)時,2)
配對比較包括比較每對可能的處理對時(計劃外比較或多重比較程序)。使用何種類型的比較取決於調查的目的。應優先考慮有計劃的比較。研究人員需要考慮是否真的需要進行所有可能的處理方法成對比較(Petersen,
1977; Onofri et al., 2010)。如果我們決定應用多重比較程序 (MCP),我們應該更加謹慎地選擇
ANOVA 檢定。植物研究人員經常使用最小顯著性差異 (LSD) 檢定。Gomez
和 Gomez (1984) 建議,當比較的數量少於
6對時,應該對所有可能的比較使用 LSD 檢定。LSD值與處理次數相關。因此當實驗包含大量處理時,不建議進行
LSD 測試。在這種情況下,處理之間的太多差異可以被認為是顯著的。當處理數量不大時,該測試對於計劃比較也是正確(Hoshmand,
2006)。
與其他
ANOVA 測試相比,LSD
測試允許獲得更多的顯著的差異。為了更自信地得出結論,建議使用更保守的測試。在 1970
年代,Decan的多範圍測試 (DMRT)
被廣泛用於 MCP。在受到批評之後,Student-Newman-Keuels
檢定被引入到實驗統計。Tukey 測試應該是
LSD 測試的一個很好的替代方案(Chew,
1976; Madden et al., 1982; Maindonald, 1992; Onofri et al., 2010)。當研究人員檢查定量變數(例如肥料用量)時,應應用迴歸分析而不是
ANOVA來獲得肥料用量增加或減少對於作物產量之間的關係。
多年來的實驗數據分析
通常植物實驗進行一年以上。它使研究人員能夠得出更有效的結論,並預測所調查的手段在不同的氣象條件下,會表現出什麼樣的影響。研究人員無法預測氣象條件,因此在此類實驗中將年份視為隨機變數。多年來將
ANOVA 應用於此項實驗,我們尋求:
1) 研究的變數是否有顯著差異?
2) 不同氣象條件下的調查結果是否穩定?
因為多年來實驗的 ANOVA 分兩個階段完成:
1) 執行每年數據的 ANOVA,
2) 處理的顯著性 ×
年代交互作用被計算。如果建立了顯著的相互作用,則應檢查其自然性質。
子抽樣和重複量測
在許多情況下,植物研究人員從每個地區塊的多個區域收集數據,例如,每個地區塊隨機抽取四個 1
平方米的正方形的植物產量。每個正方形的數據不應被視為真正的重複,因為來自同一地區塊的數據不是獨立的。如果實驗者打算使用所有數據,則可以進行裂區變異數分析,將處理作為“主區塊”,將正方形作為“子區塊”。當在多個深度進行土壤採樣時,裂區變異數分析的應用可以作為調查的解決方案。在這種情況下,土壤深度可以被視為子區塊。植物研究人員經常及時重複量測以獲得因變數的縱向數據。
在這種情況下,不應使用簡單的二因素變異數分析,因為此類數據不符合獨立性假設。裂區變異數分析的應用可能是此類數據統計分析的解決方案。將處理作為“主區塊”,將時間作為“子區塊”(Onofri
et al., 2010)。農作物的連續收穫通常在農藝實驗中進行。可以通過以下方式對此類實驗數據進行統計分析:
1) 使用所有數據集並應用裂區變異數分析(處理作為“主區塊”,收穫期作為“子區塊”)
2) 計算每次收穫的 ANOVA和所有調查期的總結數據。對於最後一種情況,應總結相同複製的數據。
迴歸和相關分析
當研究定量變數時,檢測處理方法之間差異的顯著性並不是很重要。更重要的是建立自變數和因變數之間的關係。例如施肥量增加和植物產量之間的關係。經常使用簡單線性迴歸
(SLR)。直線方程表示兩個變數之間的關係。繪製點的圖形可以顯示迴歸線的類型(Maindonald,
1992),以作為相關分析的結果,與相關係數 (R)
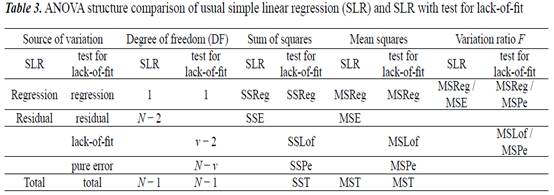
相比,現在更經常使用決定係數 (R2)。在探索迴歸和相關分析的結果之前,應檢查兩個變數之間關係重要性。SLR
的 ANOVA 結構見表 3。
在重複實驗的情況下,應使用 F 檢定檢查缺失去適當配值(Tamhane,
2009;Welham et al., 2015)。應用此程序,殘餘變異分為失適配和純誤差變異,並計算兩個
F 檢定:迴歸和失適配(表 3)。如果
F 檢定表明顯著性缺乏適配,我們得出結論,SLR
模型對這些數據不正確,我們應該尋找建立其他迴歸模型。失去適配檢定的結果必須在方法部分說明。
表
3. 普通簡單線性迴歸 (SLR) 和
SLR 與失適配檢定的 ANOVA 結構比較
植物研究中有很多案例,線性迴歸無法表達兩個變數之間的真實關係。例如,當增加除草劑劑量時,作物產量可能會增加至一定水準。但由於較高的除草劑劑量對作物的損害可能會導致產量下降。如果散點圖視覺分析表明曲線關係,則應對此類數據應用非線性迴歸模型。執行多項式模型,特別是高階模型看起來非常有吸引力,因為曲線很好地遵循數據趨勢,決定係數的顯著性非常高。多項式模型的應用,始終應與所研究關係的生物學意義相關。迴歸和相關關係可能不顯示所研究變數的生物學關係。研究人員的責任是選擇合適的迴歸模型來表達被檢查變數之間的關係。在選擇合適的迴歸模型時可以探索一些建議:
1)應優先考慮更簡單的模型,因為這增加了重複調查時獲得相似關係的可能性。
2)選擇顯示更高顯著性關係的模型。
3)注意決定係數較高的模型。
4)模型應支持解釋已建立關係的生物學。
展示研究成果
基本統計指標。
研究數據表示的基本原則是每個值都應該有其變異性的指示。在僅應用基本統計數據的情況下,變異性度量可以是標準差
(SD)、標準偏差 (SE)、變異係數
(CV)、差異值標準偏差 (Standard error of difference,
SED) 和信賴區間 (CI)。這些可變性指標含義不同,應正確使用。
研究人員可以使用 SD 和 CV
來顯示採樣值的變異性。SE 表示平均值的變異性和通過重複採樣獲得相似值的可能性。SED
與自由度一起使用。使用 CV 檢定我們可以判斷兩個群體之間差異的顯著性。
多年來的多因素實驗和實驗的結果。
在多因素實驗的情況下,應提供有關因素作用顯著性的資訊。如果研究人員需要顯示更多的交互結果,可以提供帶有自由度、F
比、概率值的 ANOVA 表。
不建議提供完整的 ANOVA
表。例如平方和或均方值對於解釋研究結果並不那麼重要。只有在不存在顯著交互作用的情況下,才能呈現因子的主效應。如果我們有幾年相同實驗的結果,則當處理和季節之間的相互作用未建立時,可以呈現不同年代來的平均值。
迴歸和相關分析的結果。
如果對具有重複的調查數據進行迴歸分析,則應僅提供處理方法。迴歸方程的參數應與標準偏差一起標明。變數之間關係的顯著性,通常與方程參數或迴歸線一起表示。
展示轉換後的數據。
數據轉換給研究結果的呈現帶來了一些不便,因為轉換後的值與原始尺度不同。這代表著變異性的統計指標不能與原始數據一起使用。另一方面,原始規模的數據應在研究出版物中進行解釋。可接受的建議可能是:反向轉換平均值為員使單位,並用字母表示顯著性檢定的結果。但在這種情況下,不可能指示平均值的可變性參數。另一種解決方案可以是在兩個尺度上並行數據表示、反向轉換數據成自然單位和具有可變性指示參數的轉換數據。這種做法的缺點是表格更複雜,需要更多空間。更多關於數據表示的建議可以在
Maindonald (1992)、Onofri et al. (2010)
和 Welham et al.(2015)撰寫的出版物找到。。
最後的評論
正確的統計應用使研究人員能夠獲得可靠的實驗結果並在作物研究中產生高品質的出版物。為此研究人員應不斷研究統計學應用文獻,如有需要,可在實驗開始前諮詢實驗統計學專家。在調查的各個階段使用統計原理。 |