中興大學 生物系統工程研究室 陳加忠

資料來源:

https://edis.ifas.ufl.edu/publication/SS548

介紹

使用肥料的建議包含幾個重要因素，包括肥料形式、來源、施用時間、放置和灌溉管理。肥料推薦的另一個重點是要施用的特定營養素的量。最佳施肥量是通過多年、多個地點、多個品種等進行的廣泛田間試驗以確定的。儘管施肥量很重要，但應將施肥量視為整個施肥管理計劃的一部分。本文著重於如何確定最佳肥料施用量其背後的研究原則，包括實驗和解釋研究結果，以實現最佳作物產量和品質，以及最小的環境影響。我們使用佛羅里達州蔬菜作物研究中的例子。如何解釋結果與如何進行研究一樣重要。

本文的目標包括州推廣專家、郡推廣教員以及從事營養、農用化學品和作物生產研究的專業人員。作者假設讀者了解基本的概率和統計。本出版物中提供的統計資訊，目的在展示肥料試驗所涉及的過程。統計數據及其計算的解釋超出了本文檔的範圍。

實驗

施肥量研究的目標是確定獲得商業作物產量所需的肥料量。該產量具有足夠的品質，在經濟上對種植者來說是可以接受。在佛羅里達州，這些類型的研究採取了略有不同的方法。具體取決於是否涉及對所關心的養分進行土壤測試。例如在沙質土壤上使用氮 (N) 進行的速率研究不涉及土壤測試。但使用磷 (P) 或鉀 (K) 進行的速率研究會涉及。就沙質土壤上的氮而言，研究人員假設從土壤中供應的氮最少可以滿足作物的養分需求。在 P 或 K 的情況下，經過適當校正的土壤測試將顯示是否可能對養分產生反應（例如產量和果實品質）。最好在特定養分含量低的土壤上進行速率研究，以便可能產生最大的作物反應並且可以模擬該反應。

正確的實驗設計和統計數據分析對於結果解釋十分重要。研究始於一個假設或一組假設。一種可能的假設是，施氮肥對產量沒有影響。這個假設被稱為虛無假設，通過一個實驗來評估作物產量對一系列氮肥的反應。該農田可能對氮肥的添加產生很大的反應。

研究人員應用了一系列肥料用量。這些肥料用量被認為可以捕捉到作物產量反應的可能程度。始終包括無肥料處理。沒有實際施肥的作物反應，用以證明和量測土壤供應的影響。在某些情況下，足夠的養分或至少一小部分作物養分需求可能來自土壤。而在其他情況下，養分可能來自灌溉水。

研究人員可能會決定將季節性肥料的總量分成不同的施用量。這可能是對所研究作物的推薦做法。多次施用避免了由於降雨事件而造成的潛在大量肥料損失，特別是對於在土壤中移動的養分。通常對於肥料的時間和放置，所有處理速率的處理方式相似。以盡量減少與速率的任何混淆影響。

在生長季節，研究人員可以使用整片乾燥的葉子和/或新鮮的葉柄汁液對植物進行營養濃度採樣。這些樣本將幫助研究人員，證明產量的反應與植物的營養狀況有關。通常不使用土壤樣品，因為樣品內可能包含肥料顆粒。或者如果通過條帶或滴灌帶施用肥料，則可能存在在哪裡取樣的問題。在該季節拍攝的照片可用於記錄生長和潛在的植物缺乏症狀。

在適當的收穫時間量測感興趣的作物反應，通常是可銷售的產量。對於蔬菜，根據美國農業部等級標準對果實進行評估，以檢測施肥對果實品質（大小、顏色、糖含量等）的任何影響。產量以每生產面積的主要商業單位表示（例如，28 磅箱/英畝、42 磅板條箱/英畝、蒲式耳/英畝、噸/英畝等）。原始數據應繪製在散點圖（圖 1）中，以深入了解反應的類型和幅度。繪製原始數據允許研究人員檢查明顯的非典型數據點，這些數據點可能說明數據輸入過程中的某個地方的錯誤。

圖 1. 作物對施氮肥的理論（非實際量測數據）反應。每個 N 比例有 5 次重複（一些數據點隱藏在其他數據點後面）。注意隨著最初幾次施氮量的增加，產量迅速增加，然後趨於平穩，並且可能表明過度施肥導致產量下降。另外，請注意零施肥有一些產量，在這種情況下約為最大產量的 20%。我們將使用術語“相對收益率”來表示該最大收益率的百分比。在 150–200磅/英畝 N之後，似乎沒有進一步增加產量。這個例子用於說明目的；通常在田間試驗中，重複之間存在更多差異，尤其是在給肥率較低的情況下

收集和檢查數據後，使用變異數分析 (ANOVA) 對它們進行統計分析。施肥對產量有顯著影響嗎？ ANOVA 在研究人員在評估施肥量對幾種作物的可能影響的情況下特別有用。在這裡，研究人員感興趣的是品種對肥料的反應是否不同，這將通過 ANOVA 表中的顯著交互項顯示出來。如果肥料處理效果顯著，那麼研究人員將希望使用有時稱為“模型”的數學方程以圖形方式呈現結果。

在化肥率實驗中，化肥率被稱為連續變數，因為除了研究人員在實驗中選擇使用的比率之外，還有許多可能的比率。使用 ANOVA，特別是如果實驗以因子排列方式排列處理，是測試處理效果和交互作用的好方法。施肥量的主要影響可以進行多項式對比，這是一種確定總體反應中是否存在線性或二次分量的統計方法。然後可以將迴歸方法應用於連續變數，以開發一個方程式來解釋反應中的顯著趨勢。

具有 5 次重複和 9 個 N 比率的隨機完整塊 N 實驗設計（圖 1 中的數據）其 ANOVA 統計表明，一種或多種 N 比率處理，在統計學上與其他處理不同（表 1）。在這種情況下，我們的虛無假設將被拒絕。由於 ANOVA 表包含幾個變異數分量的估計值，因此這些ANOVA表應包含在研究稿件中，但很少包含在內。例如其他研究人員在總結大量類似研究時可能能夠使用此資訊。雖然簡單地報告平均值和處理效果對於簡單的研究報告或演示文稿是有益的，但此方法不包含變異數量測值，而 ANOVA 表則包含。

處理意義

研究人員無法研究每一種可能的實驗處理（速率）或處理組合。此外，進行研究的領域存在自然變化。田間有機質、土壤 pH 值或水分可能存在變化，所有這些都可能導致與 N 處理無關的產量反應變化。因此概率的概念開始發揮作用。觀察到的產量差異是由於地塊之間的自然變化所導致的可能性有多大？這種固有的可變性是藉由數據的統計分析，有助於從生產系統中的所謂“噪音”或隨機誤差中找出最可能由施氮肥處理引起的差異。如果我們重複應用，稱為複製的處理，我們可以估計自然變異的相對量。實驗應始終包括複製，作為設計合理的實驗的一部分。該實驗將通過同行評審過程。變異數分析是我們用於此分析的數學工具。使用此統計工具，我們可以測試由於處理效果引起的變異，與偶然引起的變異的相對比例。

 農業研究中使用普遍接受的概率水準0.05 (5%)。當變異數分析表明沒有這種差異時，可能存在真正差異的概率。這個概率水準是科學家願意接受的錯誤水準。換句話說，真正的差異是如此罕見，以至於幾乎沒有什麼實際問題。如果實驗重複 20 次，我們的假設將有 20 分之一的機會不會被拒絕。換句話說，如果 ANOVA 表明一種或多種處理方法之間存在差異，我們 95% 確信這種差異是真實的效果。我們稱這些差異為“顯著”差異。如果 ANOVA 檢測到處理平均值之間的顯著差異，那麼我們拒絕我們的虛無假設。

在“現實世界”中，發現沒有顯著差異有兩個主要含義。首先，這代表著農民不應該有興趣每年花費額外的錢，只是為了獲得真正作物反應的罕見可能性。這些不合理的開銷會降低盈利能力。第二個含義是不需要時對作物施肥時，對環境的潛在負面影響。

關於處理差異的一種常見誤解需要澄清。例如，假設進行了一項實驗來測試氮肥率對番茄產量的影響，並且變異數分析發現大於 5% 的概率水準，種植者使用比率和較低推薦比率之間沒有顯著差異。這一發現代表著發生真正處理差異的機會非常罕見。我們可以確信種植者可以降低商業化肥用量。對於種植者和推薦的比率，實際平均值可能分別為 2,950 和 2,920 箱/英畝。可以向不了解統計數據的人提出一個論點。即 30 箱/英畝的“差異”是“價值”600 美元（30 箱，每箱 20 美元）。而這個數額將超過以種植者支付的添加肥料金額。這個結論是錯誤的，因為變異數分析表明兩種處理方法之間沒有顯著差異。因此對肥料反應的適當表示是兩種方法的平均值（即每英畝 2,935 箱）。換句話說，農場的其他因素對產量的影響大於施肥量。

一個更複雜的實驗可能是測試兩個品種對氮肥的反應。在這裡，ANOVA 用於檢驗N比率的主效應、品種的主效應以及品種對N比率反應的交互作用的顯著性。取決於N比率和品種是否存在相互作用（即品種對N比率的反應不同），有兩種結果。如果沒有交互作用，則可以使用兩栽培品種平均對N比率平均值。如果觀察到相互作用，則必須分別評估每個品種的反應。

反應的數學描述模型

在統計方面，施肥量研究採用了不同水準的定量變數，即施肥量。如果變異數分析表明顯著的 N 處理效果，如表 1 所示，那麼研究人員將希望隨著數學模型的發展進一步評估反應。可以在變數水準的整個範圍內對定量變數的反應進行統計檢查，並且可以計算對實際應用於現場的比率之間的反應。在大多數肥料實驗中，一組 4 到 5 個肥料水準加上零比率肥料控制，對於大多數模型來說就足夠了。結果可以通過方程式或模型以圖形方式呈現。如果進行了與第一次類似的第二次實驗，該模型可用於預測結果。模型通常是通過迴歸分析發展的。

可以將各種模型適稱到一組數據以解釋反應。線性模型可以解釋在測試的施肥量範圍內以直線向上或向下繼續的反應。線性反應可能代表著選擇的處理範圍不足以確定最大（或最小）產量。二次反應是典型的作物產量，其中反應隨施肥量增加，至產量接近最大值，但隨後可能以更高的速率降低。換句話說，在某一點上，增加肥料不會導致產量顯著增加。二次模型通常還具有線性分量，這代表著隨著肥料用量從低用量增加到中等用量，產量也會增加。在某一點上，增產率開始趨於穩定或下降。

線性和二次模型是用於解釋作物對肥料反應的最簡單的方程式，只要研究的主要興趣是最大化產量，它們就可以很好地為科學家服務。然而今天肥料研究還有其他目標，包括經濟和環境問題。一些研究人員探索了解釋作物對肥料反應的不同模型。研究發現，二次模型會導致高估源自對肥料反應的肥料建議（Cerrato & Blackmer, 1987; Hochmuth等, 1993a, 1993b,1996; Willcutts等, 1998）。如果研究的目標是選擇施肥量作為推薦，那麼如果將模型中的最大值作為推定的推薦值，則二次模型通常會預測更大的施肥需求。最大產量平均值並不總是，與由較低施肥量產生的一種或多種平均值顯著不同。如果我們檢查圖 1 中的數據圖，我們可能會預測在 150磅/英畝或更高的施肥量之間的產量差異很小。已經確定了其他模型，這些模型會導致較低，但農藝學上可接受的推薦施肥量，從而節省肥料費用並降低可能危害環境的過度施肥的風險。這些模型包括邏輯和線性高原模型。使用圖 1 中的數據，這三個模型如圖 2、圖 3 和圖 4 所示。

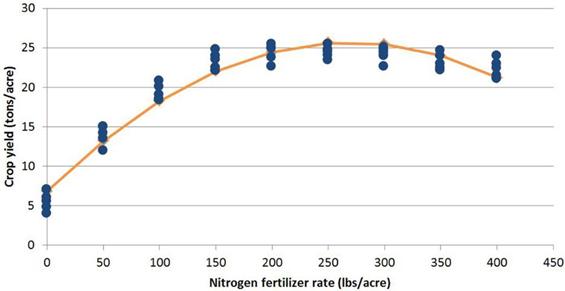
圖 2. 二次模型。產量（噸/英畝）= 6.86 + 0.14N - 0.00026N²。在 270磅/英畝 N時，最大產量 = 25.7 噸/英畝

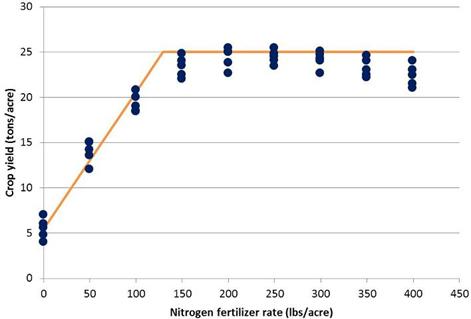
圖 3. 線性平台模型。 N<129磅/英畝（Should點）的產量（噸/英畝）= 5.5 + 0.151N，N>129磅/英畝的產量= 25 噸/英畝（plateau）

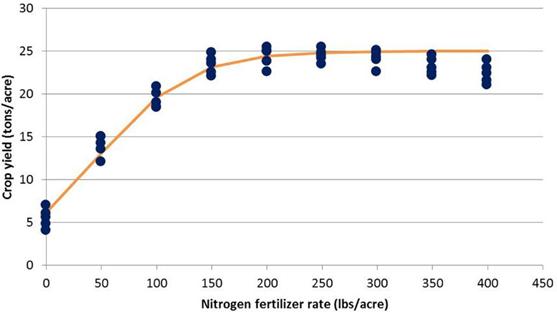
圖 4. Logistic 模型。產量 (噸/英畝) = 25 /( (1 + exp (1.12 – 0.0242N))。90% 最大產量 (25 噸/英畝) 產量 (22.5 噸/英畝) 發生在 137磅/英畝 N. 95% 最大產量（23.8 噸/英畝）發生在 168磅/英畝 N

 研究人員使用統計數據和數學模型作為工具，來幫助解釋作物對肥料的反應。我們應該記住，模型是工具，我們應該小心使用它們。此處描述的三個模型已適稱圖 1 中首次顯示的相同數據集。從變異數分析中我們知道作物對肥料的反應顯著。但變異數分析不能確定哪種施肥量更好。但是如果我們只關注模型的參數，每個模型都會講述不同故事。農藝和園藝作物反應研究中最常用的模型是二次模型（圖 2）。二次模型很容易通過電腦統計軟體套件推導出來，大多數研究人員在他們的研究生訓練中都熟悉它。此外，二次模型很容易區分以顯示峰值產量及其相關的施肥量。

僅依賴二次模型的問題出現在檢查平均產量與施肥量的關係上。可以通過正交對比表明，收益率趨於平穩。此外，這種平衡發生在肥料用量低於二次模型得出的峰值產量的情況。在一個具有環保意識的社會中，也許研究人員不應該簡單地將二次模型最大值，解釋為假定的肥料推薦率。

科學家更頻繁使用的可選模型是線性平台模型（圖 3）。該模型還產生關鍵模型參數、高原和肩點。高原說明了作物產量對肥料的反應趨於平穩的概念。然而作為推定的肥料推薦，線性高原模型肩點可能被認為過於保守。

最近在佛羅里達州對蔬菜進行的幾項研究表明，如果單獨使用二次和線性高原模型會面臨挑戰（Hochmuth等, 1993a, 1993b）。這些研究人員建議使用線性平台模型中的肩點與二次模型中的峰值之間的中點作為推定的推薦率。對於我們的數據，這個中點是 200磅/英畝的氮肥。

第三種模型（圖 4）為邏輯模型，由 Overman 及其同事在研究農作物和蔬菜作物時提出（Overman 等, 1990, 1992, 1993; Willcutts等, 1998）。邏輯模型是二次和線性平台模型之間的合理折衷。首先這個模型說明了收益遞減規律。隨著養分比例的增加，產量會增加，直到出現收益遞減的區域。其次該模型的斜率並不異常陡峭。三、函數不經過原點；因此不會預測到負產量，也不會在零肥料添加的情況下預測零產量。因此該模型解釋了原生土壤肥力。這些特性使邏輯模型對於提出避免施肥不足或過度施肥的肥料建議特別有用。

在典型的農藝或園藝作物產量反應數據中，很少有在宣布的最大產量的 90% 和 100% 之間存在顯著差異（概率 = 5%）。選擇最大產量的 95% 來推定推定的推薦施肥量將是一種保守的方法，以確保最合適的施肥量會在考慮環境風險的情況下產生有利可圖的產量。

使用上面的數據集，肥料推薦的考慮因素包括以下內容：

1.二次模型：預測的峰值作物反應為 25.6 噸/英畝，270磅/英畝 N。

2.線性高原模型：高原產量為 25 噸/英畝，肩點施肥量為 129磅/英畝 N。

3.Logistic 模型：95% 的最大產量（25 噸/英畝）發生在 168磅/英畝 N，97% 的最大產量發生在 190磅/英畝。

上面的列表顯示，根據應用的保守程度，推定的肥料推薦範圍可能在 129 到 270磅/英畝 N 之間，相差 100%。選擇線性平台的肩點和二次模型的峰值之間的中點，或者使用邏輯模型採用保守的 97% 最大產量，會產生類似的結果。該分析產生了大約 200磅/英畝 N 的推定肥料建議。選擇 200磅/英畝而不是 270磅/英畝，因為該建議不會導致產量損失，但可以節省 70磅/英畝的肥料。這既是經濟上的節省，也是從環境中真正去除肥份負荷。

佛羅里達實際研究的一個例子

上圖有助於說明研究和數據呈現的原則。佛羅里達州的實際數據呢？佛羅里達州已經對蔬菜進行了幾項研究，評估了各種模型對施肥的產量和水果品質反應。其中一項研究是用西瓜進行的（圖 5）。

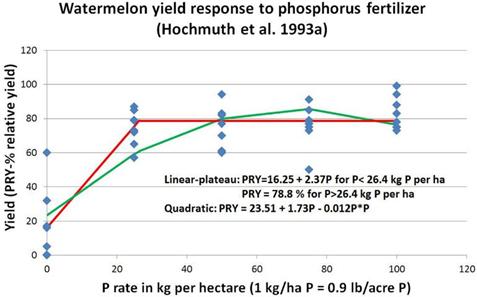
圖 5. 二次和線性高原模型的數據圖表，用於描述佛羅里達州東北部同一農場研究中西瓜對磷肥的反應。注意重複之間的差異，尤其是在零 P 處理的情況下。

在西瓜研究中，線性高原的肩點出現在 26.4 kg/ha P 或大約 53 lb /acre P₂O₅ 處。二次模型最大產量出現在 75 kg/ha P 或 150 lbs /acre P₂O₅的情況下。數據的統計分析（ANOVA 和對比）顯示 50 至 200磅/英畝 P₂O₅ 的產量沒有顯著差異。肩值處於急劇減產的邊緣，低於 53磅/英畝 P₂O₅，但二次最大產量出現在過度施肥的情況下。該研究論文的作者提出使用線性高原肩點和二次最大點之間的中點作為合理的折衷給肥建議。在這種情況下，建議可能是大約 100磅/英畝 P₂O₅。與目前針對 Mehlich-1 P 濃度低或極低的土壤推薦的 160磅/英畝 P₂O₅相比，該建議將大大節省磷肥。

使用邏輯模型（圖 6）得出的結論類似於使用線性平台模型的二次最大值和肩點之間的中點。使用 97% 的最大產量將導致大約 55 公斤/公頃 P 或 115磅/英畝P₂O₅的肥料推薦量。

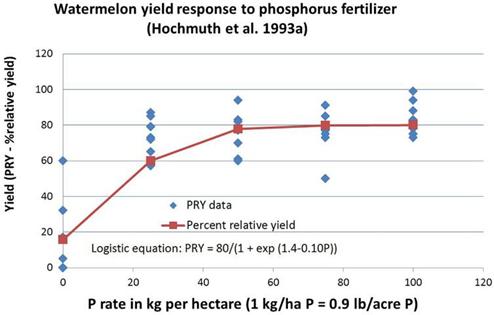
圖 6. 佛羅里達州東北部農場研究中描述西瓜對磷肥反應的邏輯方程式。

使建議更接近反應曲線的保守側除了環境之外還有其他原因。有許多關於過度施肥的研究報告，尤其是氮肥，會對產量和果實品質產生負面影響。施肥量過高導致產量略有下降，再加上額外施肥的成本，可能會導致農場利潤大幅下降。此外研究結果已發表在經由同行審查的文獻，記錄了過度施肥會降低水果和蔬菜的品質參數（Hochmuth等, 1996, 1999）。

關於百分比相對收益率 (RY) 的一些評論

作物反應是作物所面臨的整個生產系統的許多不同方面的綜合。在一個季節完成的研究，受到整個季節作物整合過程的影響，以及一些先前的影響者，例如來自作物殘株或土壤有機質的氮礦化。與由不同研究小組進行的不同實驗相關的作物反應問題，通常用於不同的目的。每個單獨的實驗中，觀察到的作物產量將顯示出變化。以原始單位繪製來自許多實驗的所有數據，會產生一個散點圖，這使得一般解釋非常困難。在眾多研究中，一種可用於了解作物對施肥反應的方法是相對產量百分比。在特定季節的特定實驗中獲得的最高產量被指定為 100% 相對產量。所有其他產量的計算方法是將觀察到的產量除以最高實際產量，並以百分比表示。

以這種方式轉換原始數據增加了相對收益率查看的靈活性，這已被使用一個共同的規模。這種轉變的價值在於，研究人員可以了解特定作物在許多季節、地點和生產作業中對肥料添加的反應。應謹慎使用相對產量，以避免過於強調這種數據轉換和結果圖。例如使用來自多個實驗的所有 RY 值進行後續迴歸可能會產生誤導，尤其是在計算實際產量時。然而注意到施肥量超過一定範圍後，所有反應之間的變異性降低，變得非常明顯。

在這個轉換過程中有許多假設。主要假設是，我們在 RY 圖中注意到的大部分或全部反應是由肥料引起的。支持和反對這一假設的爭論很多。在總結這場爭論時，Black (1992) 指出，當使用 RY 圖來探索跨年、季節和其他生產實踐的變化時，可以認為該假設是有效的。 Black 提醒讀者避免對 RY 圖進行額外的統計評估，部分原因是其統計特徵（非常態分佈），並且對添加肥料的產量反應的真實形狀是於地點特定。 RY 圖概括了土壤、肥料、氣候和植物相互作用的特定地點的變化。如果 RY 圖不用於涉及實際產量和進一步解釋的後續迴歸分析，則可以避免這種概括的問題。

對於那些對統計感興趣的人，這種類型的轉換，還具有基於選擇最大產量的加權因子。同樣這個權重因子做出了上述假設，並且通過僅在視覺基礎上使用 RY 圖，而不試圖通過其他方式進一步統計迴歸分析，將其降低到微不足道。 Black (1992) 指出，雖然這些反對意見值得注意，但 RY 圖可以成為肥料研究的有用工具。

為了進一步說明百分比相對產量方法的有用性，圖 7 中繪製了西瓜產量。請注意，所有實驗中的產量都會增加，然後在 100 到 200磅/英畝 N 之間趨於穩定。當前的 UF/IFAS N推薦值為 150磅/英畝 N。雖然此圖未用於設置 UF/IFAS 推薦值，但該圖表明該推薦值是合理的，並得到研究的支持。

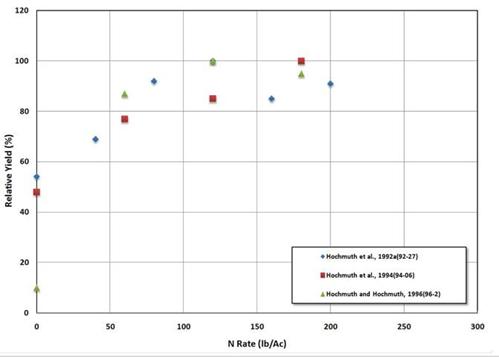
圖 7. 在佛羅里達州的幾項研究中，滴灌西瓜對增加氮含量的反應的相對產量百分比。報告所示年份後括號中的數字是進行該實驗的年份