中興大學 生物系統工程研究室 陳加忠

Tavares LF，Carvalho AMX，Machado LG。Rev Bras Cienc Solo。 2016; 40：e0150246。

摘要：幾乎所有科學論文中使用的實驗統計方法對於更清晰地解釋農業科學中的實驗結果都是至關重要的。但是由於，對這些方法的錯誤使用可能導致研究人員得出錯誤或不完整的結論。本研究的目的是評估土壤科學中實驗的特徵和統計方法的使用品質，以促進更好地使用統計方法。為此目的，隨機選擇了2010年至2014年之間發表的200篇文章，這些文章僅涉及對於土壤的肥力，化學，物理，生物學，用途和管理進行抽樣研究和研究。使用包含28個問題的問卷來評估實驗的特徵，使用的統計方法以及這些方法的選擇和使用品質。大多數被評估的文章都提供了在野外條件下進行的研究的數據，所有論文中有27％涉及通過抽樣進行的研究。大多數研究沒有提及檢驗以驗證常態性和異質變異性，並且大多數使用Tukey檢驗進行平均值比較。在具有因子結構的處理方法中，許多研究都忽略了這種結構，並在沒有因子結構的情況下比較了數據，或者進行了相互作用的分解而未顯示或提及相互作用的重要性。幾乎沒有採用裂區設計的論文都考慮過因子結構，或者將其視為裂區設計。在進行迴歸分析的文章中，只有少數文章測試了非多項式適合模型，沒有一篇報導了對迴歸缺乏適合的驗證。因此，所評估的文章反映了較差的通用性，在某些情況下還反映了實驗設計和統計分析方法選擇中的通用性錯誤。

介紹

統計分析方法是用於實驗和觀測科學的定量技術，用於評估不確定性及其對自然現象的實驗和觀測解釋的影響（Steel等，1997； Zimmermann，2004）。實驗統計方法是更好地解釋農業科學實驗結果的基礎，並且幾乎在所有當前的科學論文中都使用。但是，將統計方法錯誤地應用於實驗數據分析可能會導致研究人員得到不完整或錯誤的結論。反過來，這可能會阻礙了對於文獻中這些主題的評論，從而延緩科學知識的發展。

儘管實驗統計在土壤科學中很重要，但是在選擇統計方法方面仍然存在很大的困難（Bertoldo等，2007）。有一些研究是從農業科學的不同角度評估了這些困難。例如，就平均比較測試（MCT）的方法使用而言，Horticultura Brasileira雜誌中的35％文章和Pesquisa Agropecuária Brasileira中的57％的文章分別被分類為“不正確或部分正確”和“不適當” （Santos等，1998； Bezerra Neto等，2002）。

這些研究還強調了評估和討論其他反復出現的困難其重要性，這不僅是為了更好地使用MCT，而且是為了支持在未來的論文中，更好地使用統計方法。因此，需要對以下問題進行更多討論：例如理解研究中涉及的因素的類型，處理的性質和結構，選擇實驗設計，檢測異常值的使用測試以及適當選擇迴歸模型。這些和其他方面是實驗設計中必不可少的理論決策，可以使論文章獲得更好的方法論支持。

由於大多數學術知識都來自實驗數據，因此正確解釋數據就變得十分重要。根據Alvarez V和Alvarez（2013）的觀點，科學寫作的有效性和可靠性基於正確使用統計推論。因此，研究人員具有實驗計劃到數據的統計分析的知識，對於實驗成功和結果可信度至關重要。考慮到這一點，本研究的目的是評估實驗的特徵以及土壤科學中用於正確使用統計方法的品質。

材料和方法

隨機選擇2010年至2014年之間在巴西期刊上發表的200篇文章（Acta Scientiarum –農學，生物科學雜誌，Ciência Rural，Pesquisa Agropecuária Brasileira和 Revista Brasileira deCiênciado Solo，從每本期刊中選擇40篇文章。它們僅涉及通過對土壤的肥力，化學，物理，生物學，用途和管理進行抽樣的試驗和研究。所選期刊的評級為Qualis-Capes B1或更高，並且在出版與土壤科學相關的研究方面具有悠久的傳統。由於文章是從各期刊中隨機選擇的，因此與發表的年份並沒有得到平均體現。評估中採用的方法與Lúcio等人使用的方法相似（2003），Bertoldo等（2008a）和Lucena等（2013）使用問卷調查。準備了一個包含28個問題的問卷，分為與實驗特徵，使用的統計方法以及這些方法的選擇和使用品質有關的問題。在並非所有變量反應都經過相同統計分析方法的研究。根據每個研究的目的，僅考慮最重要的變量反應。在對文章進行評估之後，將數據製成表格，包括計算問題答案的頻率。

與診斷涉及實驗環境（田間，溫室或實驗室），處理結構（因子設計），實驗設計（完全隨機，隨機區集，抽樣研究，裂區或裂區區集）的特徵有關的問題區集），處理的數量和性質（定性或定量），重複次數，分析重複的使用以及實驗的持續時間。在本研究中，廣義上使用“設計”一詞，包括完全隨機，隨機區集，裂區，分割區和其他實驗佈置。另外，表述“抽樣研究”與LiraJúnior等人(2012)使用的“抽樣研究”相同。或Alvarez V和Alvarez（2013）使用的“抽樣設計”。在本研究中將分析重複理解為是從多個測量中獲得的與所使用的統計方法的診斷有關的問題涉及對常態性和同質性條件的驗證，變量的轉換，數據的遺失以及變方分析的執行的描述。它還涉及提及所使用的軟體，提出的分散度量，所應用的MCT以及迴歸和相關分析的使用。

有關診斷統計方法使用品質的問題涉及結構化處理分析中的一致性評估，因子設計部署的表示標準，迴歸分析中的顯著性水準指示，MCT使用評估以及評估裂區和裂區區集中的實驗分析的一致性。

結果

實驗特點

分析的許多文章都包含在野外條件下進行的研究（73％），隨後是在溫室和其他環境中進行的研究（表1）。在大多數研究中，作者提到使用隨機完整區集設計（RCB），並且大多數現場研究都是在區集中進行的。另一方面，在溫室中，大多數實驗都是以完全隨機設計（CRD）進行的。在分析的文章中，使用RCB在溫室中進行7.5％，使用CRD在田間進行17.5％（表1）。

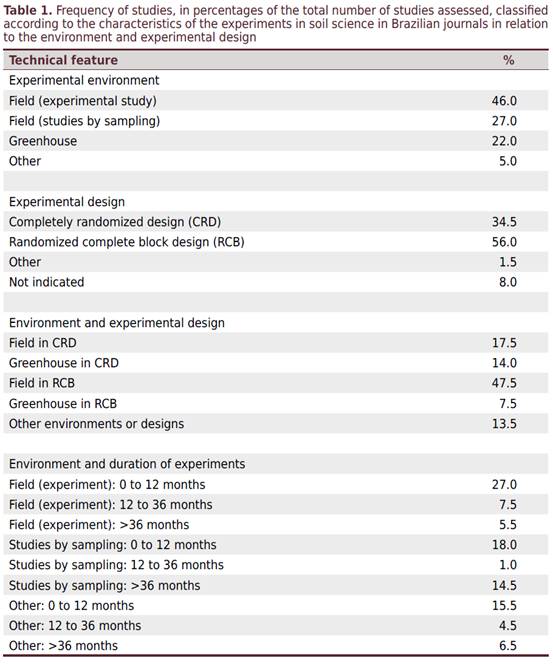
大量的論文（27％）是作為田間研究進行的，它們假定以前存在的情況為“處理”以抽樣研究，系統抽樣研究或是觀測研究進行。因此處理並沒有的真實複製或其中的隨機化（表1）。此外，大多數論文（60.5％）對應於短期研究，其中最長是評估12個月的處理效果。在長期研究中（三年或更長時間），大多數與抽樣研究相對應（表1）。

評估中的大多數論文都包括相對較小的實驗，最多12種處理和最多4次重複（72％）。只有6.5％的論文包含超過36種處理的實驗（表2）。只有1％的研究僅進行了兩次重複實驗，只有4.5％的論文提到使用了八次以上的重複實驗（表2）。大量文章（6.5％）沒有報告所使用的重複次數。此外，只有2％的人報告使用分析重複法來評估一個或多個評估的屬性（數據未顯示）。

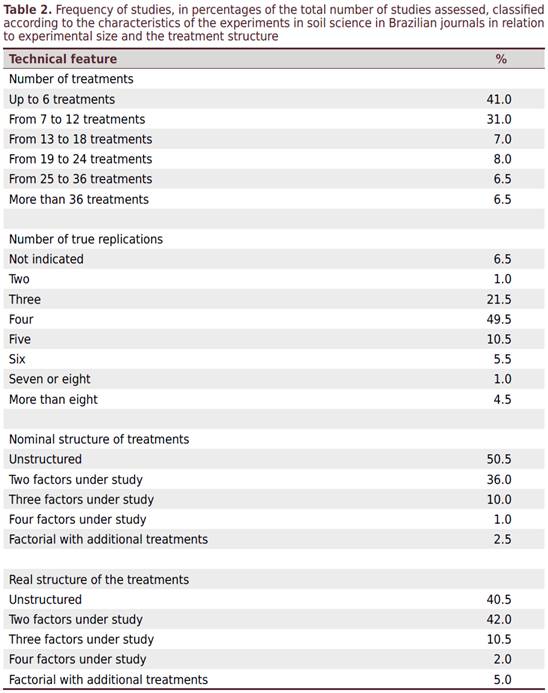
評估的論文中有一半（50.5％）不考慮或認為不必考慮因子結構（表2）。但是，在對這些論文中提出的結果進行再分析時，觀察到非結構化處理的頻率降至40.5％。在結構化實驗中，大多數不考慮額外處理，就認為已是雙重或三階因子，而一小部分因子實驗則有進行了額外處理（例如3×5 +1）

使用的統計方法以及這些方法的選擇和使用品質

大部分評論文章都提到了變方分析（ANOVA）的使用（表3），儘管只有19.5％的人提出了一些變方分析結果（表4）。此外，在大多數研究中，並未提及或未進行檢驗以驗證殘差的常態性（92.5％）和變異量的同質變異量（93.5％）（表3）。只有4％的論文提到了變量的數據轉換以滿足這些預設（參數測試的假設）。

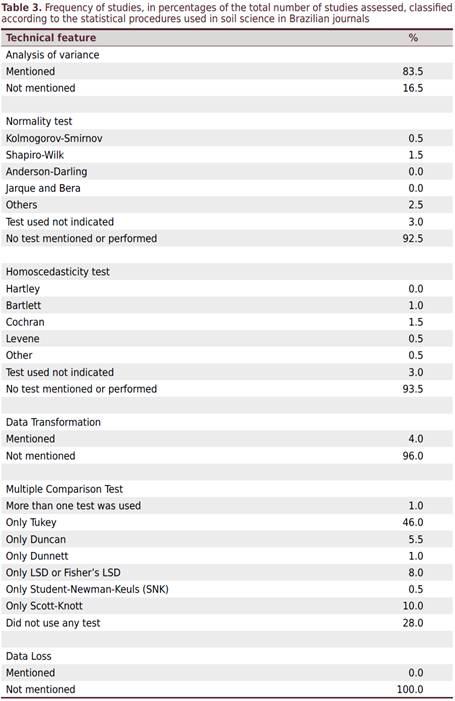
在所評論的文章中，有66％的人提到使用的軟體，其中SISVAR被引用最多，其次是SAS，SAEG和ASSISTAT（數據未顯示）。所評論的研究均未報告數據遺失或使用異常值測試（表3）。大多數研究僅將Tukey檢驗用於平均值的多次比較（46％），然後是Scott-Knott檢驗，Fisher的LSD檢驗和Duncan檢驗。使用Student-Newman-Keuls（SNK）測試僅完成了0.5％的研究（表3）。一些研究使用了涉及兩種以上平均值（5％）的對比（數據未顯示）。在70％的情況下，MCT的使用分類為適當，將9％的分類為部分適當，將21％的分類為不合適（表4）。大多數被分類為“不合適”的案例都涉及使用Duncan或Fisher LSD測試。少數研究是在更適合迴歸分析（四個或更多定量水準）的情況下仍然使用MCT。

在50.5％的論文中，作者並未將實驗視為因子設計。但是，實際上，其中約10％具有某種類型的結構（表2）。最常見的情況涉及雙因子結構。在這種情況下，將評估期，土壤層和評估時間作為處理方法進行了結果分析，但是在報告的方法中並未對此進行描述。在處理為因子結構的論文中，有12.5％忽略了該結構，並將所有處理方式進行了比較（表4）。在所有這些情況下，論文均未報告變方分析結果，例如F值對處理均方根或所研究因子的顯著性。另外，即使沒有顯示或提及相互作用的重要性，仍有20.5％的文章總是分解因子之間的相互作用（相互作用的展開）。已觀察到聲稱實驗設計（在本文中進行了描述）與實際設計（在處理中確實存在）之間的差異。在這些差異中，只有1％的研究被認為是在裂區設計中進行了實驗，而14％的研究表明了這種類型的實驗設計（表4）。

在所評估的研究中，分別進行了迴歸分析和相關分析，分別佔36.5％和17.5％（表4）。在進行迴歸分析的研究中，有11.5％未測試迴歸的整體顯著性或迴歸參數的顯著性。有14.5％的人僅使用R2中顯示了顯著性（作為迴歸的總體顯著性的指示）。有10.5％的人未顯示出迴歸的顯著性與方程式中每個參數的重要性（表4）。沒有一篇文章將迴歸殘差的不顯著性(缺少迴歸適合性）作為選擇迴歸模型的標準，並且大多數論文僅測試了線性或二次模型的適合度。

討論

實驗特點

使用RCB進行的許多野外實驗該實驗環境有關的更大異質性。主要與地面坡度有關，這通常會導致土壤肥力，水分和礦物質組成等方面的差異。 Lúcio等人也報導了這種情況（2003）在《CiênciaRural》雜誌對作物科學研究的評估也有此現象。但是研究人員需要知道實驗環境中一個或多個變化源的方向，以確保正確採用局部控制原理（水分梯度，肥力，礦物質成分和歷史用途等變因）。有了要控制影響的知識之後，關於進行區集與處理之間相互作用的可能性的理論評估仍然是可行，原來這種情況會禁止在該位置進行實驗。有趣的是，作者報告了使用RCB時要控制的內容（通常是斜率），並且他們不僅僅因為實驗是在田間條件下完成，而且選擇使用。儘管如此，重要的是也要考慮到在某些情況下即使在平坦的地形上進行RCB實驗的選擇，也可能因操作問題而合理。在這種情況下，播種，農作物和由不同的工人對每個區集進行，或者在不同的日子進行的其他活動可能產生影響。

大量的評估的研究均基於抽樣研究。這種類型的研究在土壤科學期刊上，編輯和審稿人之間產生了矛盾的觀點。因為儘管在每個區域或採樣區域內都觀察了重複值，但這些區域實際上並未重複，因此被視為偽重複（Ferreira等，2012）。 ; LiraJúnioret al.，2012）。但是，對於用於定義此類研究類型的術語尚無共識。

儘管此問題僅被視為偽重複問題（Hurlbert，1984），但是固態並未尊重處理之間隨機化的基本原理。這種失敗變得至關重要。因為每種處理的重複試驗之間沒有獨立性，並且在使用這些處理的區域之間，事先沒有保證同質性。因此，由於這些限制，這些研究顯然不能視為實驗。根據Fereiva等（2012），在這種情況下，審閱者應僅檢查是否滿足常態性和同態性的前提。如果不滿足，則建議使用非參數統計分析方法。此外根據Fereiva等（2012）和LiraJúnior等人（2012），不應僅基於這一事實而拒絕此類文章，儘管這在審稿人之間並未達成共識。在生態學領域，這種研究非常普遍，約佔田間條件下進行的研究的27％（Hurlbert，1984）。但是，重要的是，在這些情況下必須對研究策略進行正確描述，以明確表明這是通過抽樣進行的研究。此研究類型原則上不會提出實驗設計，只要符合這些條件的要求（正常性，同質性等），就不會禁止使用參數統計方法（例如變方分析，平均值檢驗，迴歸等）對它們進行分析。這些參數統計方法也被用於無法滿足基本實驗原理的社會和生態領域的研究中（Hurlbert，1984；Marôco，2011）。

同樣重要的是要考慮到，根據目前的數據，進行的大多數長期研究（三年或更長時間）都是通過抽樣進行的研究。因此要了解這些文章中得出的結論的局限性（限於特定的研究條件），可以將它們視為案例研究。大量指向同一事實的案例研究，最終可能會允許在特定主題上得出更籠統的結論，就像醫學領域一樣（An and Cuoghi，2004）。根據在土壤用途和土壤管理地區進行抽樣研究的頻率，在限於傳統技術在技術或經濟上不可行的情況下，有接受這些研究的趨勢。

長期研究使得研究人員能夠更好地評估處理，對研究中重要變量和其他互補變量的反應的效果，這可用於評估意料之外的效果。短期研究（<12個月）的頻率很高，這表明土壤研究人員對長期實驗的重視程度較低。這可能與此類研究的成本較高有關，也與大多數巴西研究人員承受的增加出版物數量的壓力有關。小型實驗（<12個處理）的優勢可能與減少時間和成本有關。在研究型的文章中，只有九篇提到使用八個以上的複製。但是，這也可以歸因於與大型實驗相比，這些實驗所允許的對更高品質的普遍理解，尤其是在更好地標準化實驗條件以及更好地標準化進行和評估活動方面（Vieira，2006）。

絕大多數（72％）包括最多重複四次的測試。 Zimmermann（2004）認為，在大多數情況下，重複的次數是根據財務資源，評估所需的時間，可用的面積或可用性工人來選擇的。實驗的重複次數非常重要，因為實驗誤差往往與重複次數成反比。但是，這種關係不是線性的，因為隨著重複次數的每次增加，實驗誤差的減小越來越小。當要求研究人員減少反應變量的可變性但又不大幅增加重複次數時，另一種選擇是對每個真實重複的重複進行量測和分析測定，這一策略在論文中仍然沒有得到充分利用。

適當數量的複製必須允許至少15個自由度的殘差（Alvarez V和Alvarez，2013）。然而，根據Pimentel-Gomes（1987）的說法，最小數字只有10。沒有數字的理論基礎，只有了解統計檢驗的敏感性與殘差的自由度有關。殘差的自由度越高，殘差均方值（實驗誤差的估計值）就越低，所應用的統計檢定力也就越高。因此，當結論基於處理之間的“相似性”時，非常重要的是殘差的自由度高，以使對統計檢驗敏感，從而降低II型錯誤的發生率。然而根據Pimentel-Gomes（2009）和Dutcosky（2013）的觀點，當結論基於處理方法之間的差異時，這一要求不一定重要。當統計檢驗未顯示差異時，殘差自由度高，則可以認為處理沒有差異。另一方面，當預計各處理之間的差異較大時，殘差的低自由度可能會使統計檢驗具有足夠的敏感性。因此，可以根據技術和財務限制來計劃一個殘差自由度小於15的實驗，並且從其結論的角度出發。只要該實驗基於“差異”而不是“相似性”，則該實驗仍然有效。

土壤科學中因子設計實驗的廣泛使用（表2），必須此與理解複雜土壤環境中對處理反應的不同因素之間相互作用的需求有關。此外，結構化處理更容易發現現像中的模式，這在所研究因素之間缺乏相互作用得到了證明。但是，包括幾個因素使統計分析的方法變得困難，以及對處理效果和這些因素之間相互作用的概述。因此建議在實驗中不要包含三個以上的因素（Vieira，2006）。在本研究中評估的文章中似乎遵循了此建議。

使用的統計方法以及這些方法的選擇和使用品質

所評論的大多數文章都沒有給出變方分析結果，這可能會降低統計推斷的可靠性（表4）。因此，一些期刊要求ANOVA結果，尤其是殘差的自由度，計算的F值或p值，以提高統計分析的可信度（Volpato，2010）。但是，這些方法不能確保可信度，尤其是在限於簡單且越來越普遍的符號類型“（F4，22 = 0.021）”時。這種類型表示與處理的自由度和殘差的自由度相對應的F的p值。例如，很容易看出這種表示法在因子設計實驗中的不滿意之處。比此表示法更重要的是簡單，準確地呈現有關結構，實驗設計，重複次數以及實驗誤差的一些估計值（例如變異係數或殘差均方根）的資訊。結果，審閱者和讀者可以檢查所指示的統計差異。

動物科學方面的大量研究比較了因子實驗的邊際平均值，卻沒有提及這些因素之間可能存在的相互作用（Cardellino和Siewerdt，1992）。這種情況清楚地表明了呈現變方分析結果的重要性。根據Bertoldo等（2008b），在CiênciaRural雜誌發表的對植物科學的226篇科學論文的後期評估中，因子設計實驗分析中所發生的大多數錯誤與研究有關，在這些研究中，作者沒有考慮因素之間的相互作用，只有邊際平均值檢定。這些結果僅在交互作用不顯著的情況下才有效，因為有必要對每個因素的水準（交互作用的分解）內進行檢定工作。

交互作用的重要性提供了有價值的信息，因為它可以啟用並驗證有關所研究因素的效果的通用性（Perecin和Cargnelutti Filho，2008）。這樣的通用性對於理解現象特別有用，並且是“通用標準”，與始終尋找分解的相互作用的概念相反。後者使人們很難理解這些標準。通用性是通過邊際平均值之間的比較獲得的。但是很容易理解到，在某些情況下，即使沒有5％的顯著相互作用，分解的相互作用也顯示了因子B的水準對因子A的每個水準的不同影響，反之亦然。為了避免這個問題，Perecin和Cargnelutti Filho（2008）建議將考慮交互作用重要性的標準（通常為p <0.05）移至更高的值，例如0.25。通過採用此標準，僅在有大量證據表明缺乏交互作用的情況下，才中止交互作用的分解，從而提高了歸納的可靠性。

沒有提及驗證常態性和均等性的前提的論文中，很令人震驚。因為如果不滿足這些條件，則可能會接受錯誤的結論。通常，當尊重實驗的基本原理時就已經假設了獨立性和可加性條件，這在通過採樣進行研究中變得至關重要。但是研究者已經達成共識。只有在數據滿足誤差獨立性，模型合乎效應的可加性，常態性和同質變異性的基本前提時，參數測試才有效。實際上，如果不滿足這些前提條件，則進一步的測試可能會產生不同結果。需要將數據進行早期的轉換以滿足此類前提條件，或如果對於數據進行了非參數測試需要。據Lucena等（2013）在對牙科研究的評估中，使用非參數檢驗數據進行了研究，其中殘差不遵循常態分佈，但在研究中被視為正常分析，因而有19%案件改變了文章中的結論。

出現大量沒有驗證這些預設條件的論文的可能解釋是，統計軟體工具在執行ANOVA時不會自動測試這些預設（Vieira，2006）。同樣重要的是，要考慮用來評估這些預設的測試之間存在差異（Jarque和Bera，1987； Lim和Loh，1996； Santos和Ferreira，2003）。這些差異，包括所採用的實驗設計在檢定力，強韌性和適當性方面的差異，可能會導致在選擇這些測試時產生一定程度的主觀性。在不確定性無法去除的情況下，用於分析預設的圖形工具可能會很有用。儘管主觀性水準最高，但仍可以做出正確的決定。

無法檢查是否滿足ANOVA預設，也可能與有異常值因而導致難以將數據適合到這些條件的頻率有關。在所有評估的研究中，均未描述或測試異常值的存在，這表明有明顯的遺漏此類信息的趨勢。根據Barnett和Lewis（1996）的說法，缺少離群值的檢測標準，這可能導致離群值的選擇有偏差。

儘管有各種檢測異常值的測試方法，但通常的建議是僅在有已知理由的情況下才應刪除異常值，也就是說，如果可以確定差異原因（Vieira，2006； Pimentel- Gomes，2009）。但是在某些情況下，這種檢查是不可行的，並且使用公正，嚴格的統計檢驗是一種非常有用但尚未探索的工具。離群值的顯著測試是Cook距離（最適合於相關分析中的配對數據），Grubbs檢驗，Dixon檢驗以及Chauvenet準則和該準則的推導，突出了ESD（Generalized Extreme Studentized Deviate）準則（Rosner，1983 ）。

Chauvenet標準是為此目的而開發的第一個標準，有時也稱為“最大標準化標準偏差標準”（Vieira，2006），是一種簡單的標準，使用時具有良好的品質，同時考慮了用殘差計算的標準偏差與均方根，而不是每個處理的殘差。然而它的推導修改了列表中的臨界值，使其變得更加嚴格，並且可以在一組中檢測到多個異常值（Rosner，1983）。該方法（稱為“通用ESD”）雖然非常嚴格，但被Walfish（2006）以及Manoj和Senthamarai-Kannan（2013）認為是用於此目的的最佳方法之一，甚至可以用於分析調整後迴歸。模型（Paul and Fung，1991）。

最後，由於流行的統計軟體中無法使用這些測試，或者由於排除了異常值導致數據不平衡，因此可能無法充分利用用於檢測異常值的測試。數據不平衡會在統計分析中產生一些複雜性，尤其是在因子實驗和RCB中（Wechsler，1998）。諸如SISVAR和ASSISTAT之類的統計軟體不會在其常規方法中分析不平衡數據（Ferreira，2008），這可能會導致錯誤地將丟失的數據替換為平均值。

大量論文表示了所使用的軟體，但是沒有正確描述所執行的過程。需要強調的是必須提及所使用的統計檢驗，而不是用於執行統計檢驗的工具（Volpato，2010）。此外，頻繁選擇SISVAR，SAEG或ASSISTAT可能表明著名的SAS和R界面不友好。大多數統計應用方法為許多不同的科學領域提供了廣泛的有用方法列表。這會提供大量的選項和命令，從而使界面更加複雜和直觀。有了這一系列選項，適用於少數領域的特定方法會混入一般方法中，並阻礙了獲得最常用的實驗統計傳統方法（例如常態性檢驗，同質變異量，變方分析，多重比較檢驗，對比和迴歸分析）。此外，檢測方法通常以非統計領域的用戶幾乎無法訪問的語言（例如SAS中的“ PROC GLM”）呈現，因此可能會導致複雜的界面，而研究生無法修改這些界面（Volpato，2010）。在這方面，考慮到特定領域的知識，有關土壤科學論文實驗特性的知識可能對開發更簡單的應用方法有用，有助於為用戶提供更友好的界面和更易用的統計語言。

Tukey測試的廣泛使用證實了Santos等人提出的結果（1998），Bezerra Neto等（2002）和Lúcio等（2003）。這是一項嚴格的測試，但檢定力（靈敏度）卻低於其他MCT（Vieira，2006）。在大多數情況下，過於嚴格並不有利，因為測試越保守，其敏感性和檢測差異的能力就越低，從而導致II型錯誤。實際上，採用MCT是由於其受歡迎程度，而不是因為它具有適應各種待測假設類型的能力，因此可能導致分析太簡化或不完整，從而導致相關資訊的丟失。

在大多數將MCT歸類為不合適的情況下，都使用了Duncan和Fisher的LSD測試。如Carmer和Swanson（1973），Perecin和Barbosa（1988）以及Sousa等人的研究所示。這些測試對實際I型錯誤（實驗方面）沒有最小的控制。 （2012年），應該廢止（Pimentel-Gomes，2009）。Student-Newman-Keuls test（SNK）儘管因其複雜性而受到Einot和Gabriel（1975）的批評，但它在高檢定力和對I型實數錯誤的良好控制之間取得了平衡（Carmer和Swanson，1973； Perecin和Barbosa，1988; Borges和Ferreira，2003）。由於這些原因，應該鼓勵使用它（Perecin和Barbosa，1988），就像其他科學領域中已經發生的那樣（Curran-Everett，2000）。 Scott-Knott分組測試（表3）的流行可能與其強韌性和產生的結果缺乏歧義性有關，這極大地促進了結果的解釋（Borges和Ferreira，2003）。此外，當要比較大量處理方法時，該測試比Tukey和SNK具有更高的功效（Silva等，1999）。然而，Borges和Ferreira（2003）觀察到的關於該測試的文獻研究很少，在部分無效狀態下的I型錯誤率很高，對此功能仍存有疑問。

通過使用F檢驗或t檢驗（Gill，1973）進行檢驗的正交對比，可以實現任何MCT更高的檢定力，並具有錯誤控制良好的實型I。這些測試在不完整的因子設計中或當感興趣的比較很少或涉及兩種以上的手段時尤其有用（Baker，1980； Alvarez V和Alvarez，2006）。但是，它們的局限性在於平均值之間的正交比較有限，並且由於大多數軟體工具不支持對其進行測試，因此很難手動執行計算。除了這些局限性之外，結果的解釋也更加困難，因為此過程的普及程度較低。

對應於四個或四個以上水準的定量因子以迴歸分析更適合比較平均值時。MCT不適合應用於該定量因子。這些結果與Cardellino和Siewerdt（1992），Santos等人提出的結果相反（1998）Bezerra Neto等（2002）和Bertoldo等（2008b）報導這種情況非常普遍。這種差異表明，在與定量處理相關的實驗中，使用MCT的觀察得到了改善。這種改進可以歸因於這些研究和其他研究對同一主題的支持，這些討論涉及在農業實驗中使用統計方法的討論。在這方面，這些研究的重要性不僅對於農業科學而且對於其他科學領域也是顯而易見的，因為它可以有助於提高用於實驗分析的統計方法的選擇品質。

在介紹實驗技術的研究中有（10％）描述了一個沒有結構的實驗，儘管在結果中將數據進行了比較，就好像它們具有因子結構一樣。在這種情況下，讀者會驚訝地在結果部分中發現它是因子設計。該結果可能因為難以充分理解研究中涉及的因素（單因素或多因素），甚至研究目的有關。因為結構是根據所提出的目標設計的。

如果一方面對進行的實驗中沒有將結構作為因子分析。而另一方面，其研究表明有因子結構，但其中很大一部分（7.5％）忽略了這種結構。在這些情況下，MCT失去了敏感性，因為處理的自由度不再被研究中的每個因子水準分解。在處理具有因子結構的研究中，我們還發現幾乎沒有仔細觀察所研究因素之間相互作用的證據，因為這些研究中超過30％分解了相互作用，甚至沒有陳述或提及相互作用的重要性。如前所述，這種情況也顯示了提出某些變方分析結果的重要性。

標稱實驗設計與實際實驗設計之間的差異主要發生在採用分區集設計的情況。但作者認為是簡單因子或裂區因子。根據各種統計手冊，可以將研究的因素（例如土壤層，時間或連續的評估年期）作為裂區進行分析（Cochran和Cox，1957； Steel等，1997； Banzatto和Kronka，2008； Dias （Barros，2009； Barbin，2013），分別是時間上的裂區和空間上的裂區。然而，其他作者則強調，Subplot中對處理的隨機性存在限制，這意味著需要將分析作為拆分區集（Pimentel-Gomes，2009； Alvarez V和Alvarez，2013）。因此，表4中顯示的關於如何分析此類實驗情況可以與主要統計手冊的不一致之處。

在這方面，值得注意的是土壤科學中的兩種常見情況：其水準涉及數小時，數年或連續的生產評估週期的因素。以及涉及層次，深度或土壤採樣位置（例如，行和行間或遠近）的因素。根據Vivaldi（1999）以及Alvarez V和Alvarez（2013）的研究，在這兩種情況下，都無法將水準完美地隨機分配給Subplot，因為第一年或週期始終在第二年之前，第二年之前是第三年，依此類推。對於通過土壤採樣評估的層，情況將非常相似，表面層顯然總是佈置在地下層之上。此外，在這些情況下，水準之間誤差的獨立性的前提必須被忽略，因為連續的時間和連續的層之間是高度相關的，並且經常在相同的實驗單位中進行評估（Vieira，2006）。當在不同的時間或評估的不同層次上沒有獨立的實驗單位出現時，獨立性問題就變得更加嚴重。但是，vivald（1999）和（Alvarez V和Alvarez）（2013）沒有提及此罕見情況，即在獨立實驗單位中隨時間或空間收集數據的情況。

裂區設計僅適用於在滿足非球形性條件的時間或空間上對同一實驗單元進行重複測量的方法（Vivaldi，1999）。否則，就需要使用多變量技術，這種技術比單變量技術更不敏感，更複雜（Vivaldi，1999）。因此在這些情況下，最簡單的解決方案是在實驗中排除這種性質的處理，將連續的時間和不同的土壤層視為不同的反應變量，而不是所研究因素的水準。它們之間的比較必須限於描述性統計。

在需要比較增長率或最高點或最低點的情況下（證明有必要將時間因素作為處理方法），可以簡單地對每次重複獲得這些速度或點數（隨時間推移），並將其作為新的變量反應進行比較（Vivaldi，1999）。但是，在某些情況下，取決於研究人員的目標，可能無法從處理結構中去除這些水準。在這種情況下，根據Alvarez V和Alvarez（2013）的說法，比使用裂區更好的選擇是通過裂區區集進行分析。在裂區分析中，主要處理方法之間比較的敏感性，降低到類似於將變量視為不同反應變量時的敏感性。

所評論文章中提供的迴歸分析結果表明，缺乏對方程式是否有意義的判別標準。對於如何以及要測試什麼以判別合適的模型幾乎沒有共識。迴歸分析用於多種目的。但是在實驗統計中，它不僅涉及檢查哪些數學模型適合該數據，還包括對該適合的解釋品質（理論意義），適合模型的重要性以及模型的含義進行評估。迴歸無法解釋的部分（包括迴歸無意義參數或迴歸殘差，或迴歸分析適合性（Alvarez V和Alvarez，2003）。

著名的實驗統計手冊都沒有提到需要通過t檢驗來測試並指出方程式中每個參數的重要性（Pimentel-Gomes，1987; Zimmermann，2004; Banzatto and Kronka，2008; Pimentel-Gomes，2009; Barbin， 2013）。但是，其他作者也支持這種方法（Nunes，1998； Alvarez V和Alvarez，2003）。重要的是要記住，例如，二項多項式方程的第二階項，儘管僅在5％以上才有意義，但不應從模型中將其排除（Pimentel-Gomes，1987）。 Alvarez V和Alvarez（2003）也支持此建議，儘管這些作者認為，即使該低乘幕的顯著性高於5％，也應指出其重要性。這對於確定每個迴歸參數的重要性，其實際需求產生了不確定性，因為僅僅表明了模型整體的重要性。並且亦證明了的非重要性的驗證性證據（通過F檢驗在F中檢驗）。或是以變方分析（ANOVA迴歸）得出關於模型選擇的相同結果。

通常，參數數量越少，適合模型（最簡化的模型）的簡單性和適合性品質之間的平衡就越好。通過實驗條件，隔離參數條件，以減少涉及兩個以上相關參數的複雜數學模型。儘管如此，多項式模型通常不足以應對自然現象（Pimentel-Gomes，2009）。對論文中適合的迴歸模型進行評估後發現，一些非線性或非二次象限被忽略了。指數模型，Mitscherech模型，S形模型以及其他模型是相對簡單的模式，僅涉及具有兩個參數的數學模型（Pimentel-Gomes和Conagin，1991）。在大多數軟體中使用這些模型執行迴歸ANOVA的困難，可能是造成這種情況的原因。

這些研究反映了通用性不佳。在某些情況下，實驗計劃和統計分析方法的選擇均存在錯誤。在某種程度上，這種情況與對某些方法的使用缺乏共識有關。但是，在某些情況下，卻很少使用非常有用的統計方法，而在另一些情況下，最流行的統計應用則不提供其使用方法或則以複雜且不直觀的界面提供它們。除了本研究中討論的統計方法外，還需要進一步討論其他一些問題，例如要提出的分散量測問題，使用非連續變量響應，轉換數據的標準，非線性迴歸模型以及常態性和同質變異性的各種測試。