|
資料來源:
https://doi.org/10.1590/S0102-053620170302
摘要
研究過程中所必須具有實驗結果的統計分析與解釋。因此希望每位研究人員先對研究主題有基本的了解。在蔬菜作物方面,這種植物相關的特性包括集約化管理和開展試驗所需的勞力高、果實成熟不均勻和試驗區的異質性,使得試驗規劃、實施和數據收集更加複雜。所有這些影響因子都是實驗中變異性的來源,因此在實驗計劃和實施階段,規劃避開這些問題是減少實驗誤差的基礎。此外,統計檢定的知識,及其使用的假設對於研究結果在統計上有效性同樣重要。此篇文章內容提出了蔬菜實驗中避免發生的變異性問題,以及減少和管理的可能性。討論了實驗中不受控制的影響,因而引起的變異性要如何替代。針對常見的實驗設計,為每種類型的處理,推薦適當的統計測試和殘差診斷技術。希望處理蔬菜作物的研究人員一起做出貢獻,能夠提供幫助研究人員的規劃,實施實驗以及分析和解釋實驗結果。
前言
對實施科學研究實驗,使用方法的相關資訊和建議有很大的需求性。在實驗工作開始時,研究人員會針對處理效果提出假設,然後通過進行實驗得出預期的答案。
實驗是研究的科學領域。實驗屬於概率統計領域。實驗研究包括規劃、實施、數據收集、分析和解釋
(Cochran & Cox, 1986; Pimentel Gomes, 1990; Steel et al., 1997; Banzatto
& Kronka, 2006, Storck等,2016)。熟悉實驗對於每個專業人士、研究人員與研究結果的使用者都很重要。該實驗為研究人員提供了支持概率。並且在已知的不確定性和誤差範圍內,允許對於不同自然現象的行為進行推論。
研究人員需要了解實驗方法才能正確地進行計劃、實施和評估實驗。並且分析和解釋實驗結果。技術人員及研究結果的使用者,必須了解如何實驗,以理解實驗,解釋其結果並評估其可靠性,允許通過適當的技術語言與研究人員交換想法。因此實驗對於直接或間接參與研究的所有專業人員都很重要。
與作物管理相關的幾個因子,都會影響最終產品的數量和品質。實驗目的是在栽培作業中。證明在關於給定的特定生產要素。有顯著性的假設。實驗是“根據假設計劃的程序,在控制條件下啟動現象的發生。目的是觀察和分析其結果與影響”(Cochran
& Cox,1986;Pimentel
Gomes,1990;Steel
等, 1997;Banzatto
和 Kronka,2006;Storck
等,2016)。因此一種新的作物管理技術只有在進行實驗測試後才能轉交給農民。同時對於其假設所提出的答案,將具有科學依據和可靠性。
計劃、裝置和實施實驗的步驟以及實驗數據的統計分析必須以嚴謹性技術科學,以盡量減少不受控制的外部影響因子的干擾。通過這種方式,這種影響將僅僅產生並導致殘餘變異量或實驗誤差。實驗誤差是歸因於只有隨機效應的變化。實驗誤差(隨機變異)如果越高,處理方法之間的差異需要越大,才能區分是否顯著(Cochran
& Cox, 1986; Pimentel Gomes, 1990, Steel et al., 1997; Banzatto & Kronka,
2006; Storck et al. ., 2016)。由於實驗計劃和實施的問題,實驗誤差經常被擴大。在這種情況下,實驗精密性低,實驗結果的可信度低。因此結果可靠性與實驗精密性直接相關。這篇論文的目的是介紹研究人員在進行農業試驗的整個過程中,必須仔細觀察的步驟內容,尤其是蔬菜作物的試驗。
實驗計劃
在這個階段,研究人員必須確定研究對象,提出解決方案,計劃實驗並詳細描述需要使用的統計程序。研究人員應該提出解決處理方案作為假設。例如具有固定效果的處理(H0:ti=0 處理彼此沒有區別,H1:ti≠0處理彼此不同)。注意影響實驗結果的不同因子(變異來源),並熟悉使用於解決假設的統計方法,考慮到所選的實驗設計和定義的顯著性水準(α
-當假設為真時拒絕 H0 的概率)。
實驗必須進行控制。即在不同處理方式的情況下,其他可能影響實驗結果的因子應盡可能保持不變。在蔬菜實驗中,除了實驗區域外,其他一些可以產生異質性的因子有:
1.在設施栽培中,試驗區所用結構的覆蓋物和遮蔭材料的重疊。
2.植株異質性,尤其在研究移植蔬菜的情況。
3.植物形態,因為高大的植物在地塊之間有利於更顯著的競爭。
4.勞力需求大,在實驗的實施和收穫過程中,可能導致作物管理和/或植物損傷的異質性。
5.昆蟲、病原體和雜草。
6.植物行內和植物行間的變化,特別是在使用田畦或床時。
7.在同一試驗區,其他作物的接近程度。
8.不均勻的成熟度和對於收穫點主觀。在蔬菜多次收穫的情況下,這些見解導致植物和收穫之間的變異性以及數據庫中過多的零。
當考慮到上述因子時,要避免大錯誤。因此實驗實施必須嚴格。管理要有規範,盡量同質化。工人合格且訓練有素。此外實驗設計應有效地減少實驗區域內的自然變異。這些控制因子導致實驗誤差的減少,並使研究人員有信心得出結論。即處理之間觀察到的變異性不是偶然發生。
基本概念
實驗單位 (EU)
或實驗區塊是應用於處理並評估其實驗效果的最小單位。定義實驗區塊的類型、數量、大小和形狀非常重要,因為它直接干擾實驗的實施。實驗區塊可能包括田地、帶土壤的盆器、苗床、植床、培養皿、試管、植物、植物葉子、機器等。區塊類型直接取決於實驗中評估的處理類型。
實驗中的區塊(P)數量取決於處理(I)和重複(J)的數量(實驗的P
= I x J)。在定義區塊的數量時,還必須考慮實驗誤差。其應該只是非控制效應引起的變異數。為了獲得均方誤差
(MSE) 的準確估計,Pimentel Gomes (1990)指出誤差自由度數量必須合理(最小為
10)。他還建議實驗應該至少有 20
個地塊,以保證合理的準確性。區塊大小與重複次數相關。一般而言,能夠確定與處理應用或處理效果評估,仍然可以兼容最小可能田區時,所需的重複次數需要確定,以保證所需的實驗精密性。
當實驗面積不是限制因子時,最好增加重複次數而不是地塊大小。重複次數的增加導致誤差自由度的增加,從而減少了殘差均方或均方誤差
(MSE)。較低的 MSE 會導致較高的
F計算值,從而在變異數(ANOVA)分析增大拒絕
H0假設的可能性。此外當 MSE
較低時,區隔處理所需的最小顯著差異值(MSD),會隨著實驗準確性的提高而下降。因此即使是處理之間的微小差異,也可以通過補充測試(complementary
test)宣布。
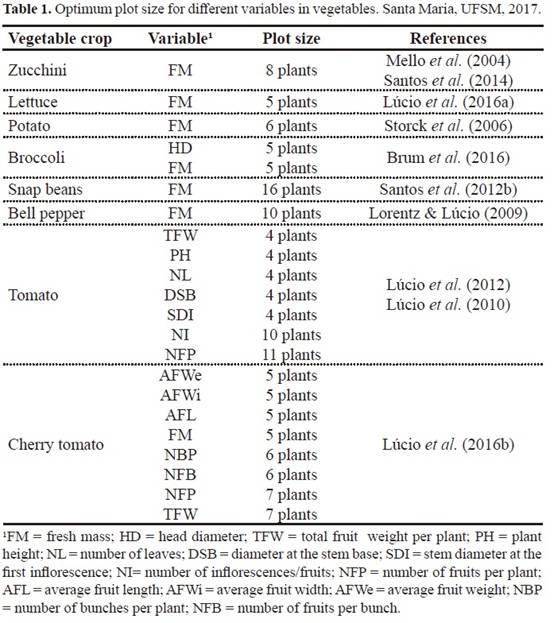
區塊大小取決於實驗材料和目標、處理次數、種子/幼苗的可用性、機械化需求、總面積、成本、時間和可用於實施實驗的勞力。區塊形狀也與實驗精密性有關。一般來說,實驗精密性隨著相對長而窄的區塊而增加,因為這種區塊形狀允許在實驗區域的均勻條件下有更多的區塊。換言之,人們可以說,最合適的地塊形狀和大小,就是導致同一組地塊之間變化最小的那種形狀和大小。地塊大小是通過均勻性測試、對照處理和均勻品質管理的實驗來估計的。在蔬菜作物中,已經進行了幾個物種的地塊面積(表1)。因此在計劃實驗時,研究人員必須使用這些資訊,以便使得他們實驗中的小區大小,具有技術與科學的依據。表1.顯示蔬菜中不同變數的最佳地塊大小。
實驗材料,即實驗單元中使用的任何材料(花盆、植物、種子、介質等),必須仔細選擇以盡可能均質。實驗材料應該與目標母群相關。通過使用同質性實驗材料,地塊也往往更同質。以方便使用不太複雜的實驗設計(例如完全隨機設計)。實驗設計越基本,實驗誤差的自由度就越大,因此實驗精密性最高。
在實驗中,我們通常使用觀察單元。這是針對實驗材料中量測和記錄觀察變數的最小部分。研究人員通常只評估實驗地塊的一部分,稱為樣本工作區域,或者只在此區塊內進行抽樣。這兩種抽樣方法之間有明顯的區別。使用樣本區域時,對區域內的所有個體進行評估,觀察變數的數值為所有單獨記錄數值的平均值。通過抽樣,隨機抽取一些有代表性的個體進行評估,觀察變數的數值也是經由個體記錄的平均值獲得。除此之外,另一個很有前景的替代方法是變異數分析
(ANOVA),因為可評估同一行內相鄰植物之間存在相互作用(邊界效應)。Santos等(2014)
表明,使用行中兩個相鄰地塊的殘留平均值作為共變數(Papadakis方法)可以減少了實驗誤差、最佳化區塊大小,和減少了區分蔬菜實驗處理所需的最小顯著差異。
在區塊中使用抽樣方法,為實驗增加了一個新的變異源(誤差),定義為取樣樣本誤差。樣本誤差在變異數分析中(ANOVA)對應於區塊中存在的變異性。因為我們是通過此區塊取樣樣本表示該區塊之結果,與實驗誤差不同。後者取樣誤差對應於區塊之間的變異性。一般而言,研究人員在變異數分析
(ANOVA)中忽略了取樣樣本誤差未將其作為額外的變異來源。因此取樣樣本的誤差最終會被添加到實驗誤差中,從而增大
MSE 估計值。為了規避此錯誤,變異數分析 (ANOVA)必須將實驗誤差和取樣樣本誤差視為孤立(彼此獨立)的變異來源。在理想情況下,區塊中的抽樣變異(取樣誤差)和具有相同處理的區塊之間的實驗誤差,應該相同且盡可能低。因此沒有顯著的影響的實驗誤差,用以表明區塊內樣本變異,和相同處理區塊之間的樣本變異性是相同的。當這種影響顯著時,區塊與區塊之間的變異性高於地塊內的樣本變異性。因此除了區塊大小外,樣本大小也應該在實驗計劃中好好地定義和描述,以防止在收集數據和以後統計分析數據中出現問題。幸運的是,針對不同蔬菜作物的適當區塊樣本,其需要規模已有多項研究可用(Souza等,2002;Lúcio等,2003,2012;Lorentz等,2004;Santos等,2010;Haesbaert等,2011)。
在實驗單元中表示隨機處理效果的評估特徵(結果)稱為觀察變數、反應變數或因變數。這種隨機變數可以是隨機離散或連續的,因此必須在實驗計劃中確定和描述(將評估什麼因變數?何時?在計畫的哪個部分?實驗單位
或個人的評估將進行?
將使用哪些設備?將使用哪種計量單位?)。在計劃實驗時,觀察到的隨機變數其定義應該是隨機離散或連續的,這也需要通知研究人員。必要時轉換實驗數據。因為根據統計模型的定義,實驗誤差應該具有常態分佈概率,ɛ ij~
N(0,σ2),讀作:“所有
ɛij
(i = 1,2, ..., I 處理, j = 1,2, ..., J重複)
均相同且獨立的常態分佈中,平均為零,具有共同變異數σ2。
實驗收集的數據,當滿足統計模型的假設時,很容易被分析。而變異數分析
(ANOVA)是最常見的。Barbin (2003)
詳細描述了瞭解處理性質的相關性,因為處理是唯一控制的變異來源,與其他來源例如實驗誤差不同。這也是為什麼在實驗計劃中,正確選擇處理和定義處理是如此重要。
實驗中的處理次數應該是滿足研究目標的最低限度需求。如果處理具有固定效應,變異數分析
(ANOVA)將估計每個處理的個體效應,並將它們相互比較。如果處理具有隨機效應,變異數分析將估計其變異數分量,這對植物育種非常重要(Cochran
& Cox, 1986; Pimentel Gomes, 1990 ; Barbin , 2003; Banzatto & Kronka,
2006; Storck et al. , 2016)。
當這些處理或因子具有定性特徵(形狀、特徵、方法、類型、物種、栽培品種等)時,以一組平均值排序的顯著性檢定方法,用於比較固定效應的處理估計值。另一方面,當處理是定量的(例如肥料或農用化學品劑量、種植或播種密度、評估時間等)時,則該應用不同模型的迴歸分析(Cochran
& Cox, 1986; Pimentel Gomes, 1990; Banzatto & Kronka,2006;Storck
等,2016)。根據Cardellino
& Siewerdt (1992),這些統計程序經常被不加分類的使用,因此破壞了可以從結果中得出的結論。因為沒有產生關於資訊的處理,例如經濟上顯著的對比,和最大技術和經濟效率點。
實驗可以評估不同數量的影響因子。評估單個因子的實驗被稱為單因子,其推斷範圍僅限於其他所有控制的變異源,都保持統一或恆定條件。為了增加實驗的推斷範圍,可以使用多因子處理,同時研究其中兩個或多個因子,每個因子具有兩個或多個水準。在這種情況下,處理由每個因子有不同水準的組合加以組成。每個因子可以具有固定或隨機效應。
因子(factorial)試驗的一個特例是裂區設計,其中試驗具有主區,其中一個因子是隨機的。主區塊被分成子區塊,其中第二個因子被隨機化(圖1)。裂區實驗有兩個誤差:一個來自主要區塊之間的變異,另一個來自子區塊之間的變異,即實驗誤差。這些變化也會影響變異數分析
(ANOVA),更具體地說是影響 F
檢定統計量的估計方法。
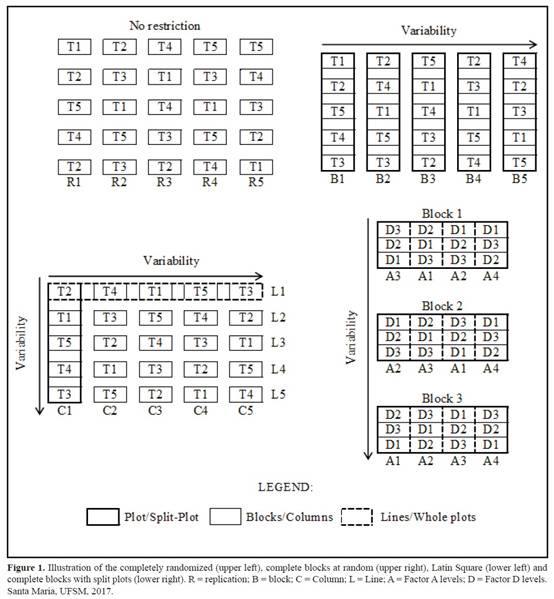
圖1完全隨機化(左上)、隨機完整區塊(右上)、拉丁方格(左下)和帶有裂區的完整區塊(右下)。R
=重複數目;B = 塊;C =
列;L = 線;A =
因子 A的水準;D = 因子
D的水準。(Santa Maria, UFSM, 2017.)。
通過增加影響因子的數量和每個因子的水準數,處理的總數目也會顯著增加,對區塊的需求也會增加,因此實驗的規模也會增加。這種擴展往往使得在均勻條件下進行實驗困難,增加了實驗誤差,降低了實驗結果的精密性和可靠性。在這些情況下,可以通過部分因子(fractionated)(不完全因子)或使用混雜技術(confounding)來減少處理次數。其中每個區塊在均質控制條件中,僅使用一些處理組合(Zimmermann,2004)。因子實驗需要評估因子之間的相互作用是否是顯著。一個因子的水準在另一個因子的水準內“展開”。在具有大量因子的實驗中,三重或更高階的相互作用可能會使分析、解釋和呈現結果變得更為困難。因此具有三個以上因子的實驗計劃,既不常見也不可取。
重複、隨機化和局部控制
為了比較處理並以已知的信賴區間進行結論,每個實驗都應遵循以下基本原則:重複和隨機化(Zimmermann,2004;Storck
等,2016)。隨機化的執行方式引出了第三個原則,即局部控制(Pimentel
Gomes,1990;Banzatto
& Kronka,2006)。因此只有在實驗單元進行重複和隨機分佈處理時,實驗在統計才會有效性。
重複是指對兩個或多個區塊應用相同的處理。重複的目的是確認個體對給定處理的反應,獲得對實驗誤差(殘差變異量)的估計值,並獲得對處理平均值的估計值。反過來隨機化是將處理隨機分配給實驗區,即每次重複中每個處理的隨機分佈,有助於殘差的獨立性。
不僅對區塊處理進行隨機化分配,而且進行任何栽培作業或進行任何實驗的評估順序也需要隨機化。隨機化目標是為所有處理提供相同概率分配到任何地塊,以消除非自願性發生向給定處理,避免在重複試驗中,系統性的支持或削弱處理。並且建立統計模型誤差和其他參數的獨立性。這也是統計模型的假設之一,並保證在解釋時實驗結果的概率,是歸因於其他因子的差異。不會使得於不同處理的反應產生偏差。
局部控制是如何將處理隨機分配到區塊,並防止區塊組之間的變化擴大成為實驗誤差。異質實驗區被劃分為更小和更同均勻的子區域,使實驗設計更高效率(Cochran
& Cox, 1986; Pimentel Gomes, 1990; Banzatto & Kronka, 2006; Storck et
al., 2016)。局部控制可以減少了實驗區域異質性對於實驗精密性的影響。
處理隨機化中使用的數量限制是根據實驗區域的異質性來源加以定義。在同質地區,有真正同質的實驗單元,對於隨機化沒有限制,因此採用完全隨機化設計。當實驗區因單一變異源而異質時,將實驗區劃分為同質子區,形成同質實驗單元區塊。在實驗設計被稱為隨機完整區塊設計。這種設計的唯一限制是需要將每個塊內的所有處理隨機化。如果實驗區的條件由於兩個變異源而異質,則需要對實驗單元進行雙重區集(blocking)。因此在隨機化處理時使用兩個限制。在這些情況下,使用拉丁方格設計。在拉丁方格中,在控制第一個異質性來源(行)的每個區塊內處理隨機化一次。在控制第二個異質性來源(列)的每個“區塊”內再次隨機化(圖1)。
一般而言,處理隨機化中的限制數量越多,與實驗誤差相關的自由度越少。因此如果限制條件不能有效地減少實驗誤差的變異,則實驗將因增加均方誤差估計值而失去效率。因此只有在有需要時才應使用區域控制(local
control)。
在種植行之間的現有變異性,是在蔬菜實驗計劃時應考慮的另一個問題。行間的變異量其異質性有兩個重要的後果:應為每一行確定最佳地塊大小(提供地塊間變異數最低的那個面積),並且實驗設計應考慮行間的變化(Schwertner等人,2015a,b)。整個實驗中使用的區塊大小,即是在最高可變異量估計值的大小(Lúcio等人,2016b)。
為了確認實驗計劃得當,研究人員應對以下問題加以解決:
1.實驗單元是否明確定義,是否代表推論母群的意圖?
2.被評估的處理是否正確選擇,它們是否反映了實驗目的?
3.試驗區的處理分配過程,是否符合試驗區的異質性?
4.重複次數是否能夠保證足夠的實驗準確性?
5.觀察變數的描述是否清晰,量測過程是否理解?
6.實驗實施所有行動和作業都得到了明確和詳細的定義?,
7.實驗數據的統計分析,是否根據處理的特點和實驗設計進行?
一旦滿足這些要求,就完成了實驗計劃。但是請記住,即使只是在該區塊內的一小部分,實驗地區之間也始終可能存在發生異質性。在這種情況下,必需有良好的判斷力、良好的計劃以及對研究對象和實驗材料的了解。建議始終嘗試協調變異性原因,因為其對減少實驗精密性是不可避免的。重要的是要減輕它們的影響,並了解可能統計出現問題的地方以及它們的干擾程度。
實施實驗
在實施實驗過程中進行的任何過程、動作或活動,都應盡可能均勻地進行,以免擴大實驗誤差。在規劃階段應該就預先已經考慮到與蔬菜作物管理相關現有特性預先知識,以保持實驗精密性。
植物的適當生長和發育,以及因此產生可靠的實驗數據,取決於實驗實施過程中充分良好的作物管理。與蔬菜作物植物發育相關的經常活動有:播種、種植和幼苗移植;疏葉、疏株和立柱;病蟲害和雜草控制;施肥和灌溉。由於集約化管理,蔬菜也需要密集的勞力。因此,產生了必須控制的兩個重要的異質性來源:勞力和所有作物進行作業所需的時間。每當作物作業涉及大量人員時,它就會成為異質性的重要來源。因此必須調整訓練參與工作的團隊,以確保在整個實驗過程中,盡可能均勻地進行作物管理。
此外由於密集性管理,許多作業無法在同一天完成。在完全隨機試驗的設計中,所有活動必須在同一天(或更少)時間內完成,並在所有實驗地塊中均勻進行。這需要訓練、效率和工作團隊的性能。在隨機的完整區塊或拉丁方格中,作物的作業可以一次在一個區塊和/或行中進行,而不必在同一天在所有區塊和/或行中進行。如果可行,每個區塊最好由同一人管理和評估。它有助於維持區塊內和/或行內的同質性。區塊和/或行之間可能出現的異質性不會影響實驗精密性,因為在這些實驗設計中,它的影響和其變異,能夠在統計模型中被預測並單獨評估。
如果機械設備經過適當校正並且操作員受過良好訓練,則機械化作業通常比手動進行作業更均勻。使用相同的操作員是保持均勻性的另一種選擇,不要忘記人員疲勞是也可能的變化來源。
最後,人工採摘是研究人員應該小心觀察的另一個重要作業。實驗期間的任何植物處理,都可能成為異質性的來源,尤其是在多次收穫的作物。訓練收穫團隊,尤其是統一識別其收穫點,有助於減少收穫物和植物之間的差異。在收穫時,建議與作物管理相同。在隨機區塊和拉丁方塊的完整區塊的情況下,每個人應負責收穫一塊和/或一行。並且如果可能,應僅一個人進行在完全隨機的設計中執行收穫作業。
因為作物作業和收穫可能成為異質性的來源,這將顯著的影響實驗精密性。為了避免這種情況,研究人員應該訓練工作團隊。根據實驗設計進行作物作業。使用與作物和其變異兼容的地塊大小,並清楚地描述收穫點和對收穫進行分組的必要性,並定義後續收穫的時間間隔。
數據統計分析
一旦計劃和實施階段完成,實驗數據的統計分析就開始。研究人員最常採用的方法是執行變異數分析
(ANOVA),然後再檢測其平均值之間是否存在顯著差異,進行事後檢定(一組平均值排序的顯著性檢定),或是迴歸分析。但是在進行變異數分析
(ANOVA)之前,必須觀察某些特性,主要是與統計假設有關。無論採用何種實驗設計,這些假設是:
1.統計模型的可加性,即參數必須是可加且獨立的;
2.ɛij是聯合獨立的、隨機的、相同而且常態分佈的。平均值為零而且具有共同變異數,ɛ ij~N(0;σ2)。所有這些假設都是有效進行統計檢定所必需具備的條件。
變異數分析
(ANOVA)
在具有兩個以上因子其平均值的實驗,變異數分析 (ANOVA)是用於檢查處理是否相等的方法。基本上變異數分析
(ANOVA)使用 F
檢定來驗證處理效果之間的差異是否是偶然。F
計算值對應於處理均方之間的比率。處理的均方用以表示處理效果之間的變異量,均方誤差 (MSE)
表示隨機變異(任何實驗固有的變異 +
實驗誤差)。因此可以理解,如果處理之間的變異是由於偶然引起的,均方誤差只有實驗誤差,則 F
值將等於 1。計算得到高的 F
值,表明處理之間的變異量大於因為偶然引起的變異量。因此處理之間確實存在差異。p值也可以被用作為決策準則。當p
值低於顯著性水準時,假設 H0被拒絕,並得出結論處理彼此不同:
當進行變異數分析 (ANOVA)時,應該回答兩個問題:實驗設計是否有效,與處理效果之間是否存在顯著差異。前面所討論過的蔬菜實驗變異性相關方面內容,對變異數分析
(ANOVA)有直接影響。實驗計劃和實施中的失敗會擴大實驗誤差,從而提高均方誤差
(SME) 的值。較高的 SME 值會降低
F 計算值,並使處理之間是否有顯著不同更加困難區分,從而增加接受 H0
的概率。即使它原本是錯誤的。
殘差分析
無論使用何種實驗設計,都必須對實驗誤差進行嚴格的分析,以檢查與原來的統計模型假設是否一致(Barry,1987)。這種分析通常集中在兩個方面:誤差是均質與服從常態分佈。應該強調的是,分析是針對誤差而不是針對觀察到的數據。這在科學刊物中很常見。為了確認這些假設,可以採用圖形分析或統計測試。
在這裡,我們展示了三種常用的殘差分析及其解釋的圖形工具(圖2):

Figure 2具有(A)負不對稱、(B)正不對稱、(C)常態分佈、(D)leptokurtic
函數和(E) platikurtic函數。各以殘差的圖形表示。(Santa
Maria, UFSM, 2017.)。
1.頻率直方圖:當數值集中在圖的邊緣時,分佈不是常態的,而是不對稱的。如果不對稱性為負,則值集中在右側(圖2a)。如果不對稱性為正,則值集中在左側(圖2 b)。峰態(Kartosis)與曲線變平有關。曲線在“尖”時稱為
leptokurtic(圖2d),當它“變平”時稱為
platikurtic (圖2e)。兩種情況都表明分佈不是常態分佈(圖2);
2.QQ圖:當觀測值承擔“弧形”的形狀(圖2a和2 b),分佈是不對稱的。當觀測值低於該線時,分佈是常態分佈,即對稱和mesokartic(圖2c)。S形值表明該曲線是尖峰厚尾或platikurtic(圖2 d和2 E);
3.Box-plot:當盒子位移到圖形頂部時,出現負不對稱(圖2a)。如果位移到圖形底部,則為正不對稱性(圖2 b)。而在集中中間時,分佈是常態的(圖2c)。窄框指向leptokurtic曲線(圖2d),而長框表示platikurtic曲線(圖2e)。
最常用於研究實驗誤差的常態性和同質性的統計檢定是:
1.常態:Anderson
Darling, Shapiro-Wilk, Kolmogorov-Smirnov;
2.同質性:Bartlett
和 Levene。Bartlett
檢定。僅在滿足實驗誤差常態性假設時使用。
兩種研究實驗誤差的方法各有優缺點。圖形分析往往更主觀,但它可以用以確定假設不滿足的原因(不對稱、異常值存在、峰態、分佈混合)。另一方面,統計測試更方便且不那麼主觀,因為其是解釋基於p值。p值越高,對常態分佈的遵守程度越高,實驗誤差同質性就越大。
滿足這些假設是執行變異數分析(ANOVA),和對一組排序平均值進行顯著性檢定的基本條件
(Barry, 1987)。如果不滿足此假設,研究人員可以轉換數據並再次進行檢定。最常見的數據轉換是平方根、對數、Arcsin
和 Box-Cox (Yamamura,1999;Couto
等,2009;Lúcio
等,2011)。如果即使在轉換後誤差仍然不是常態分佈或變得異質,則必須使用非參數分析,例如
Wilcoxon、Mann-Whitney-Wilcoxon、Friedman
和 Kruskal-Wallis (Conover,1971;Campos,1983)。
變異數分析 (ANOVA)的使用與常態分佈假設、相同變異量假設和誤差獨立性直接相關。由於異質變異量、數據庫因零值膨脹,以及變數的分佈本質
(例如,計數數據),可以上述這些假設經常被違反(McCullagh
& Nelder,1989)。從這個意義上說,在蔬菜作物實驗中,使用廣義線性模型
(GLM)替代變異數分析 (ANOVA)。這些模型由隨機分量(建立隨機變數分佈)、系統分量(建立解釋變數
因子和因變數之間的關係)與及將系統分量與隨機分量相關聯的鏈接函數組成。使用偏差分析 (ANODEV)
比較 ANOVA 統計模型。此外在
GLM 中,混合模型可用於分析數據中數據有零的模型。(Zeileis 等,2008;Zuur等,2009)。
補充測試(complementary
tests)
當檢測到在給定顯著性水準的處理之間有顯著差異時,應用統計檢定來補充變異數分析
(ANOVA),並區分處理的效果。要應用哪種補充統計分析取決於處理的性質。對於定性處理,使用一組平均值排序的顯著性檢定。對於定量處理,使用迴歸模型。最常見的補充測試是:
a) 一組平均值排序的顯著性檢定:t
(LSD)、Tukey、Duncan、Dunnett
(雙向均值比較檢定)、Scheffé、正交對比
(均值組之間的比較檢定)和 Scott & Knott
(均值聚類測試)。
b) 迴歸分析:Y(反應變數)為
X(定量處理水準)的函數的多項式迴歸。
在因子實驗中,應根據變異數分析 (ANOVA)結果進行補充分析。對於顯著的交互作用,必須對因子水準進行統計分析。當交互作用不顯著時,可使用因子的平均值。對於每種可能的情況,在雙因子實驗中採用的程序是
(Banzatto & Kronka, 2006; Storck et al., 2016)。
1.因子A(定性)和因子D(定性),非顯著交互作用:變異數分析
(ANOVA)+對一組平均值排序進行顯著性檢定,以區分因子A和D的水準。
2.因子A(定性)和因子D(定性),顯著交互作用:變異數分析
(ANOVA)+一組排序的顯著性檢定,代表著在因子A的每個水準內,區分因子D的水準。對一組排序的顯著性檢定代表著在因子
D 的每個水準中,區分因子 A 的水準。
3.因子A(定性)和因子D(定量),非顯著交互作用:變異數分析
(ANOVA)+對一組平均值排序進行顯著性檢定,以區分因子A的水準+因子D的迴歸調整因子。
4.因子A(定性)和因子D(定量),顯著交互作用:變異數分析
(ANOVA)+對一組平均值排序進行顯著性檢定,以區分因子D每個水準內因子A的水準+每個水準內因子D的迴歸調整因子。
5.因子A(定量)和因子D(定量),非顯著交互作用:ANOVA+因子A和D的迴歸調整。
6.因子A(定量)和因子D(定量),顯著交互作用:變異數分析
(ANOVA)+多元迴歸調整,通過表面反應進行圖形表示。
非線性迴歸
在多次收穫蔬菜中,非線性迴歸模型的調整非常有用,可以作為對生產進行推論的替代方法(Lúcio
等,2015,2016 d,e)。隨著收成的積累,產量在周期開始時呈指數成長,達到最大成長點(inflection
point),並在最後呈現漸近值(最大產量)。這些方面可以通過稱為成長模型的非線性模型的參數來量化(表
2)。生長模型具有具有生物學解釋的參數(α,代表漸近線,γ,代表生產率),將它們轉換為重要工具,以幫助描述隨時間推移的生產行為(Draper
& Smith,1981;Bates &
Watts,2007)。
成長模型的調整還需要觀察一些假設:誤差為常態性、同質性和獨立性。前面討論的誤差常態性和同質性的診斷可以完全用於非線性模型。關於誤差獨立性,最常用的是檢查誤差是否自相關的
Durbin-Watson
檢定。還必須進行量化模型非線性的測試,因為它們對於驗證參數調整的品質很重要。非線性越低,調整參數的品質就越高(Draper
& Smith, 1981; Bates & Watts, 2007)。
不建議在非線性模型中進行數據轉換,因為它會改變參數的數值,使它們無法使用於生物學解釋。如果不滿足誤差同質性和獨立性的假設,建議採用兩種方法:當誤差變異數異質時,通過加權最小二乘法調整模型。當誤差是相反自相關時(Draper
& Smith,1981;使用Bates
& Watts,2007)使用廣義最小二乘法。
因此,實驗的最後一步即數據分析,直接取決於計劃階段,並受實驗實施方式的強烈影響。通過適當的計劃和適當的實驗實施,收集的數據將不會受到過大的隨機變化的影響。從而與實驗目的一致,可以進行充分的統計分析。
減少蔬菜作物的變異性
影響植物和果實生長以及其成熟度和收穫時間點,其巨大變化是由環境條件的變化引起的,例如氣溫、太陽總輻射、雲量和相對濕度。蔬菜作物顯著的受這些因素影響。不管被試驗評估的蔬菜是什麼,果實不會在不同的植物中同時出現。相反,由於坐果取決於整個植物生長過程中新芽的發育,因此在植物之間其果實發育幾乎總是不相等的。因此每次收穫時,和收穫之間發生變異異質性,主要是由於某些水果的早熟或晚熟,這是由於植物生理學的變化或是不利的環境條件造成的。
識別數據的過度分散,與及檢查其原因的一個選項,可能是檢查在多個收穫條件下,觀察變數所獲得的數值。對這些數據以其擁有的概率分佈進行調整。以及在多個連續收穫所獲得的觀察值,觀察其獨立程度。這種識別使得將此類數據庫的行為加以表徵成為可能,提供有關在實驗區塊中產生的觀察變數值,其最合適方法的資訊,從而避免數據庫中過度分散的問題。另一種策略是累積每個植物的生產變數值。以積累產生值與增加量用以在觀察到的數值的行為中評估植物。從而使得能夠使用迴歸分析估計變數值。
蔬菜實驗中理想收穫點,其定義仍然非常主觀。因為收穫點往往基於商業植物部分的大小和/或顏色。並根據每種作物的不同,而有所不同。此外一些蔬菜的生產時間錯開,以允許在其生產週期內多次收穫。
在蔬菜作物多次收穫的實驗中,變異性通常很高。主要是由於在所有地塊中,每次收穫時都沒有收集到足夠的商業產品,觀察值有大量的零值(Lorentz
等,2005 ;Lúcio等,2006,2008)。這種情況經常導致殘差變異數膨脹,這使得數據庫中的過度分散。這現象在收穫期的開始和結束時,更頻繁地被觀察。此時植物處於不同的發育階段,成熟不均勻,更難以客觀地確定收穫點。
開展了大量工作來制定策略並確定最合適的程序,以便在蔬菜作物實驗中最大限度地減少數據變異性。提高多次收穫蔬菜實驗品質的最有效也是最常用的策略是,識別特定作物的地塊(表
1)和樣本數量。確定行與收穫之間的變異行為。以及轉換數據的研究。使用
Papadakis 方法來最小化數據庫中的多餘零數量的影響以免導致過度分散 (Lúcio
等,2011 ,2016 a,c;Santos等,2012
a,b,2014 ;Benz
等人al.,2015 ;Lúcio
& Benz,2017)。
有兩種方法可有效減少多次收穫的蔬菜的變異性:收穫物和植物的聚類。對幾種蔬菜的研究表明,收穫聚類減少了植物之間的變異性,減少了數據分散性,並減輕了數據庫中過多零的負面影響(Carpes
等,2008 ,2010;Lúcio
等,2011 ,2016b,c;Santos等,2012a,b,2014
;Benz 等,2015
;Lúcio 和 Benz,2017)。然而即使有收穫聚類,變異性可能會繼續增加。因為收穫“n日”的累積值與收穫“n-1日”中觀察到的值保持相同,此時植物中沒有要收穫的產品。而在另一區,其中有可收穫的產品,因此數據增加。由於植物成熟度不均勻和收穫點的主觀性,這種行為在多次收穫的蔬菜中很常見。
單獨分析收穫時在植物之間觀察到的高變異性,其一個結果是需要使用更大的地塊,包括多株植物(Lorentz
& Lúcio,2009;Lúcio等,2010、2012、2016a、b;Santos
等, 2012b, 2014)。它導致實驗區域未得到充分利用,可能會減少同一區域的處理和/或實驗數量。需要強調,如果研究人員選擇使用較小的區塊,實驗誤差會增加,從而導致實驗精密性下降。實驗誤差太高,導致難以在變異數分析
(ANOVA)中檢測處理之間的顯著差異。通過平均值比較測試(定性處理)區分處理的能力較差,以及使用迴歸調整(定量處理)的品質降低。
結語
進行實驗是一項艱鉅的任務。需要時間、資源和勞力來確認或拒絕先前定義的假設。這些假設來自於給定區域的農業作業挑戰。根據所有階段後試驗獲得的統計結論,確定了向農民推廣的實用建議。因此實驗過程應該全面進行,目的是最好地代表母群建議的意圖。
為了使結論和建議具有較高的實驗精密性和最高的可靠性,研究人員必須盡最大努力使得殘差(實驗誤差)盡可能最小。為了實現這一點,實驗必須很好的計劃和實施,以區塊內同質性為目標,使第
II 類錯誤率也盡可能小。有關實驗的主題和材料以及實驗技術的知識是試驗的基礎,更是成功的關鍵。 |