|
資料來源:
https://doi.org/10.7554/eLife.48175
摘要
為了更廣泛的努力,使科學研究結論有更加可靠的啟發,我們編制了一份在科學文獻中最常出現的一些的統計錯誤清單。這些錯誤源於無效的實驗設計、不恰當的分析,和/或有缺陷的推理。我們就作者、審稿人和讀者如何識別和解決這些錯誤提供建議,我們希望將來能避免這些錯誤。
關於提高研究可重複性的必要性已經有很多論文(Bishop,
2019;
Munafò等,
2017;
Open Science
Collaboration, 2015;
Weissgerber等,
2018),並且有很多人呼籲改進統計訓練分析技術(Schroter等,
2008)。在本文中討論了科學文獻中常見的十個統計錯誤。儘管許多研究人員強調了透明度和研究倫理的重要性(Beck,
2016;
Nosek等,
2015),但在這裡討論了統計的疏忽,這些疏忽在論文中顯而易見。在論文提出主張,但是不是從數據中得出,這是顯而易見。儘管是錯誤的,但經常以表面價值看待論文(Harper
& Palayew, 2019;
Nissen等,
2016;
De Camargo,
2012)。防止發表錯誤結果的最合適的檢查點,是期刊的同行評審過程,或者可以在預印本發表之後進行的在線討論。本評論的主要目的是為審查者提供幫助識別和管理這些常見問題的工具。
所有這些錯誤都是眾所周知的,並且有很多關於它們的文章,但它們繼續出現在期刊上。以前對該主題的評論傾向於關註一個錯誤或幾個相關錯誤:通過討論十個最常見的錯誤,我們希望為研究人員提供一種資源,供研究人員在審查手稿或評論預印本和已發表論文時使用。這些指南也有助於研究人員計劃實驗、分析數據和撰寫手稿。
我們的名單起源於the
London Plasticity Lab的期刊俱樂部,該俱樂部討論神經科學、心理學、臨床和生物工程期刊上的論文。我們作為讀者、審稿人和編輯的經驗,進一步驗證了這一點。儘管此列表的靈感來自與神經科學相關的論文,但此處描述的相對簡單的問題與任何使用統計學來評估的科學學科都是相關。對於我們列表中的每個常見錯誤,我們將討論錯誤是如何產生的,解釋作者和/或審查者如何發現它,並提供解決方案。
我們注意到這些錯誤通常是相互依賴的,因此一個錯誤可能會影響其他錯誤,這代表著其中許多錯誤無法孤立地糾正。此外通常不止一種方法可以解決這些錯誤。例如我們在關注頻率論參數統計解決方案中,經常有我們不討論的貝葉斯解決方案(Dienes,
2011; Etz & Vandekerckhove, 2016)。
為了促進對這些問題的進一步討論,並就如何解決這些問題合併建議。希望對這些常見錯誤的更多認識,將有助於作者和審稿人在未來更加警惕,從而使錯誤變得不要那麼常見。
1.缺乏足夠的控制條件/組
問題
在多個時間點量測結果,是科學中一種普遍的方法,以評估干預的效果。例如在檢查訓練的效果時,通常會探究行為或生理指標的變化。然而結果量測的變化可能是由於研究中,與操作(例如訓練)本身沒有直接關係的其他因素所造成的。在沒有干預的情況下重複相同的任務,可能會導致干預前和干預後量測結果之間的變化。例如由於參與者或實驗者只是習慣了實驗環境,或者由於與實驗相關的其他變化隨時間流逝。因此對於任何研究隨著時間的推移實驗操作對變數的影響,將這種實驗操作的效果與控制操作的效果進行比較是十分重要的。
有時包括一個對照組或條件,但設計或實施不充分,並不包括可能影響跟踪變數的關鍵因素。例如對照組通常不會接受“假”干預,或者實驗者對干預的預期結果沒有視而不見,導致效應量膨脹(Holman
et al., 2015)。其他常見的偏差來自運作一個小型控制組,該控制組的能力不足以檢測到跟踪的變化。或者一個具有不同基準線量測的控制組,可能會導致虛假的相互作用(Van
Breukelen, 2006)。同樣重要的是,控制組和實驗組同時抽樣並隨機分配,以盡量減少任何偏差。理想情況下,受控組操作在設計和統計能力方面應與實驗操作相同,並且僅在特定刺激維度或操作下的變數上有所不同。這樣,研究人員將確保操縱對跟踪變數的影響大於隨時間變化的變化,而不是由所需操縱直接驅動。因此在變數隨時間進行比較的情況下,審查者應始終要求進行控制。
如何檢測它
結論只是基於單組數據得出的,沒有足夠的控制條件。控制條件/組不考慮操作固有任務的關鍵特徵。
研究人員解決方案
如果實驗設計不允許將時間的影響與干預的影響分開,那麼關於干預影響的結論應作為暫定的。
2.解釋兩種效果之間的比較,而不直接比較它們
問題
研究人員通常通過指出干預在實驗條件或組中產生顯著效果,而在控制條件或組中相應的效果不顯著。基於這兩個獨立的測試結果,研究人員有時會建議實驗條件或組中的效果大於對照條件下的效果。這種類型的錯誤推理很常見但不正確。例如,如圖
1A 所示,兩個變數 X 和
Y,每個變數在 20
名參與者的兩個不同組中量測,在統計顯著性方面可能具有不同的結果:A
組中兩個變數之間相關性的相關係數可能具有統計學意義(即p≤0.05)。而類似的相關係數對於
B 組可能沒有統計學意義。即使兩個變數之間的關係對於兩組而言幾乎相同(圖
1A)也可能發生這種情況),因此不應推斷一種相關性大於另一種相關性。
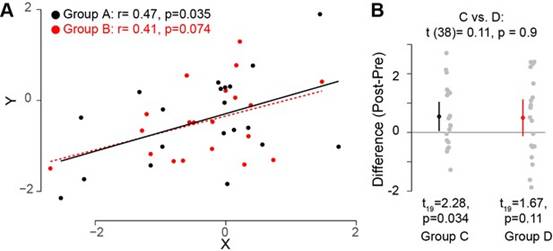
圖1解釋兩種效應之間的比較而不直接比較它們。
(A)
對兩組
A 和 B 量測了兩個變數 X
和 Y。很明顯,這兩個變數之間的相關性在這兩組之間沒有差異。但是,如果比較……
查看更多
在評估在兩個不同組中量測的干預效果時會出現類似的問題。干預可能在一組中產生顯著效果,但在另一組中不會產生顯著效果(圖
1B)。然而,這並不代表著兩組之間的干預效果不同。
實際上,在這種情況下,兩組並沒有顯著差異。只能通過兩種效果之間的直接統計比較得出結論,干預的效果與對照干預的效果不同。因此與其運行兩個單獨的測試,不如使用一個統計測試來比較兩種效果。
如何檢測它
當在沒有進行統計比較的情況下就兩種效應之間的差異得出結論時,就會出現這個問題。這個問題可能發生在研究人員在沒有進行必要的統計分析的情況下,進行推斷的任何情況。
研究人員解決方案
研究人員在想要比較組時應該直接比較它們(審稿人應該將作者指向,以清楚地解釋問題及其影響,Nieuwenhuis等,
2011)。兩組的相關性可以與蒙特卡羅模擬進行比較(Wilcox
& Tian, 2008)。對於組比較,變異數分析可能是合適的。儘管非參數統計提供了一些工具(例如,
Leys & Schumann, 2010),但這些工具需要更多的思考和定制。
3.誇大分析單位
問題
實驗單元是可以隨機獨立分配的最小觀察值,即可以自由變化的獨立值的數量(Parsons et al.,
2018)。在傳統統計中,這個單位將反映自由度(df)。例如在推斷小組處理結果時,實驗單位是被測試的受試者數量,而不是每個受試者中進行的觀察次數。但不幸的是研究人員傾向於混淆這些措施,從而導致概念和實際問題。從概念上講,如果沒有明確識別合適的單位來評估為現象變異,統計推斷是有缺陷的。實際上這會導致大量的實驗單元(例如,所有受試者的觀察次數通常大於受試者的數量)。當df增加時,判斷統計顯著性的關鍵統計臨界值會降低,如果存在真正的影響(統計檢定力的增加),則更容易觀察到顯著的結果。這是因為對測試結果有更大的信心。
為了說明這個問題,讓我們考慮一項針對
10
名參與者的干預研究的簡單的前後縱向設計,研究人員有興趣使用簡單的迴歸分析來評估他們的主要指標與臨床狀況之間是否存在相關性。他們的分析單位應該是數據點的數量(每個參與者
1 個,總共 10 個),結果為 8
df 。對於df = 8,實現顯著性的臨界
R 值(α 水平為 05)為
0.63。也就是說,任何高於臨界值的相關性都是顯著的(p≤0.05)。如果研究人員將參與者的前後量測值結合起來,他們最終會得到df
= 18,臨界 R 值現在為 0.44,從而更容易觀察到具有統計顯著性的效果。這是不合適的。因為它們混合了分析單元內部和分析單元之間,導致它們的度量之間存在依賴性,給定主題的預分數不能在不影響其後分數的情況下改變,這代表著它們真正只有
8 個獨立的df 。這通常會導致將結果解釋為顯著,而事實上證據不足以拒絕。
如何檢測它
審查者應考慮適當的分析單元。如果一項研究目的在了解群體效應,那麼分析單元應該反映受試者之間的差異,而不是受試者內部的差異。
研究人員解決方案
也許解決這個問題的最佳解決方案是使用混合效應線性模型,其中研究人員可以將受試者內的變異性定義為固定效應,將受試者間的變異性定義為隨機效應。這種越來越流行的方法(Boisgontie
r& Cheval, 2016)允許將所有數據放入模型中,而不會違反獨立性假設。然而它很容易被濫用(Matuschek
et al., 2017),並且需要高級的統計理解,因此應該謹慎地應用和解釋。對於簡單的迴歸分析,研究人員有幾種可用的解決方案來解決這個問題,其中最簡單的方法是分別計算每個觀察值的相關性(例如
pre、post),並根據現有的df解釋
R 值。研究人員還可以對觀測值進行平均,或分別計算前/後的相關性,然後平均得到的
R 值(在應用R 分佈的歸一化後,例如
r-to-Z 變換),並相應地解釋它們。
4.虛假相關
問題
相關性是科學中用於評估兩個變數之間關聯程度的重要工具。然而,參數相關性(例如 Pearson's R)的使用依賴於假設。這些假設很重要,因為違反這些假設可能會導致虛假相關性。如果兩個變數之一存在一個或多個異常值,則最常出現虛假相關。如圖
2的第一行所示,遠離分佈其餘部分的單個數值可能會誇大相關係數。虛假的相關性也可能來自集群,例如如果來自兩組的數據在這兩個變數不同時合併在一起(如圖
2的底行所示)。
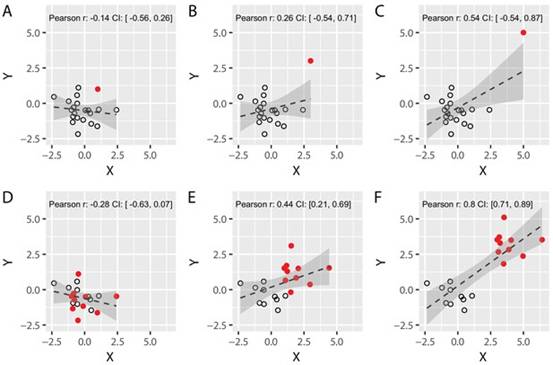
圖
2虛假相關:單個異常值和子組對 Pearson 相關係數的影響。
(A-C)我們用
19 個樣本(黑色圓圈)模擬了兩個不同的不相關變數,並添加了一個額外的數據點(實心紅色圓圈),其與主要人群的距離為
需要注意的是,異常值很可能會提供符合您試圖發現的現象規律的真實觀察,換句話說觀察本身不一定是虛假的。因此應該非常謹慎地考慮刪除“極端”數據點。但是如果這種真實的觀察有可能違反您的統計測試的假設,那麼它實際上就變成了虛假的,因此需要使用不同的統計工具。
如何檢測它
審稿人應特別注意未附有散點圖的報告相關性,並考慮在丟棄數據點時是否提供了充分的理由。此外如果將數據匯總在一起,審查者需要確保考慮組間或條件間的差異。
研究人員解決方案
在大多數情況下應該首選穩健的相關方法(例如bootstrapping,
data winsorizing, skipped correlations),因為它們對異常值不太敏感(Salibian
-Barrera & Zamar, 2002)。這是因為這些測試考慮了數據的結構(Wilcox,
2016)。使用參數統計時,應篩選數據是否違反關鍵假設,例如數據點的獨立性以及異常值的存在。
5.小樣本的使用
問題
當樣本量較小時,只能檢測到較大的效應,從而對真實效應量的估計留下很大的不確定性。並導致對實際效應量的高估(Button
et al., 2013)。在使用 alpha=0.05
的顯著性臨界值的頻率統計中,所有統計測試的 5%
將在沒有實際效果的情況下產生顯著結果(假陽性 false positives; I
類錯誤)。然而研究人員更有可能認為具有高係數(例如 R>0.5)的相關性比適度相關性(例如
R=0.2)更可靠。如果樣本量小,這些錯誤報告的影響量就很大,從而產生顯著性謬誤:“如果樣本量小,效果量那麼大,那可能是真的。If
the effect size isthatbig with a small sample, it can only be true.
(This incorrect inference is noted inButton
et al., 2013 (Button
et al., 2013
中指出了這種不正確的推論)。更大的相關性並不是兩個變數之間存在更強關係的結果,這僅僅是因為對實際相關係數的高估(這裡,R
= 0)。在樣本量較小的情況下總是會更大。例如,當對兩個 N = 15
的不相關變數進行採樣時,模擬的假陽性相關性大致在 |0.5-0.75| 之間。而當使用
N = 100 對相同的不相關變數進行採樣時,會在 |0.2-0.25|
範圍內產生假陽性相關性。
樣本量較小的設計也更容易遺漏數據中存在的效應(II
型錯誤)。對於給定的效應量(例如,兩組之間的差異),用更大的樣本量檢測效應的機會更大(這種可能性稱為統計檢定力)。因此對於大樣本,降低了在實際存在效應時未檢測到效應的可能性。
與小樣本量相關的另一個問題是樣本的分佈更容易偏離常態性,而有限的樣本量使得通常無法嚴格檢驗常態性假設(Ghasemi
& Zahediasl, 2012)。在迴歸分析中,與分佈的偏差可能會產生極端異常值,從而導致虛假的顯著相關性。
如何檢測它
審稿人應嚴格檢查論文中使用的樣本量,並判斷樣本量是否足夠。應特別標記基於有限數量參與者。
研究人員解決方案
來自小樣本的單個效應大小或單個
p 值的價值有限,審稿人可以將給Button
等 (2013)推薦給研究人員來說明這一點。研究人員應該提供證據證明他們已經有足夠的能力檢測到開始的影響,例如通過先驗統計能力分析的呈現,或者執行他們的研究的複制。檢定力計算的挑戰在於,應該基於來自獨立數據集的效應大小的先驗計算,而這些數據在審查中很難評估。貝葉斯統計提供了確定事後識別效果的能力的機會(Kruschke,
2011)。在樣本量可能有限的情況下(例如對稀有臨床人群或非人類靈長類動物的研究),應努力提供重複(在病例內和病例之間)並包括足夠的對照(例如建立信賴區間)。為評估案例研究提供了一些統計解決方案(例如,Crawford
t 檢驗;
Corballis,
2009)。
6.循環分析
問題
循環分析是任何形式的分析,它回顧性地選擇數據的特徵來表徵因變數,從而導致結果統計檢驗的失真(Kriegeskorte等,
2010)。循環分析可以採用多種形式和形式,但它本質上涉及回收相同的數據以首先表徵測試變數,然後從它們進行統計推斷,因此通常被稱為“雙浸,double
dipping”(Kriegeskorte等,
2009)。最常見的是,循環分析用於使用追溯性且與統計結果固有相關的選擇標準來劃分(例如sub-grouping,
binning)或減少(例如定義感興趣區域、去除“異常值”)完整數據集。
例如,讓我們考慮一項針對給定操作的神經元群體放電率的研究。在比較整個人群時,在操作前後沒有發現顯著差異。然而研究人員觀察到,一些神經元通過增加它們的放電率來反應操縱,而其他神經元則通過對操縱作出反應而降低。因此他們通過根據基線觀察到的活動水平對數據進行分類,將人口分成亞組。這導致了顯著的相互作用效應,那些最初產生低反應的神經元表現出反應增加,而最初表現出相對增加的活動的神經元在操作後表現出降低的活動。然而這種顯著的相互作用是扭曲的選擇標準和統計偽影
(statistical artefacts)。Regression to the
mean, floor/ceiling effects組合的結果,因此可以在純噪聲中觀察到(Holmes,
2009)。
另一種常見的循環分析形式是在因變數和自變數之間創建依賴關係。繼續上面的例子,研究人員可能會報告操作後細胞反應之間的相關性以及操作前後細胞反應差異之間的相關性。但是這兩個變數都高度依賴於操縱後的措施。因此在操作後量測中偶然激發更強烈的神經元可能會相對於獨立的操作前量測顯示出更大的變化,從而誇大相關性(Holmes,
2009 )。
當結果在統計上獨立於零假設下的選擇標準時,選擇性分析是完全合理的。然而循環分析會引入噪聲(任何經驗數據所固有的)來誇大統計結果,從而導致統計推斷失真並因此無效。
如何檢測它
循環分析以許多不同的形式表現出來。但原則上,只要統計檢驗量測因選擇標準而偏向於被檢驗的假設,就會發生這種情況。在某些情況下,這是非常清楚的。例如如果分析基於為顯示感興趣的效果或固有相關效果而選擇的數據。在其他情況下,分析可能會很複雜,需要對選擇和分析步驟中的相互依賴關係有更細緻的理解(例如,參見Kilner
,2013中的圖 1 和Kriegeskorte等,
2009中的補充材料 HYPERLINK "https://elifesciences.org/articles/48175"
\l "bib36")。審稿人應該警惕不可能的高效應量,這在理論上可能不合理。和/或基於相對不可靠的量測(如果兩個量測的內部一致性較差,這會限制識別有意義的相關性的可能性;
Vul et al., 2009)。.在這種情況下,審稿人應向作者詢問選擇標準與利益影響之間獨立性的理由。
研究人員解決方案
提前定義分析標準並獨立於數據將保護研究人員免受循環分析。或者由於循環分析通過“招募”噪聲來擴大所需效果,最直接的解決方案是使用不同的數據集(或數據集的不同部分)來指定分析參數(例如選擇子組)。並用於測試您的預測(例如檢查子組之間的差異)。這種劃分可以在參與者級別(使用不同的組來確定減少數據的標準)或在試驗級別(使用不同的試驗但來自所有參與者)進行。這可以通過自舉方法在不損失統計能力的情況下實現(Curran-Everett,
2009)。如果合適,審稿人可以要求作者進行模擬,以證明感興趣的結果與噪聲分佈和選擇標準無關。
7.分析的靈活性:p-hacking
問題
在數據分析中使用靈活性(例如切換結果參數、添加協變數、未確定或不穩定的預處理管道、事後異常值或受試者排除;
(Wicherts
等, 2016)增加了獲得顯著 p
值的概率(Simmons
等, 2011)。這是因為規範統計依賴於概率,因此您運行的測試越多,您遇到誤報結果的可能性就越大。因此在給定的數據集中觀察顯著的
p
值並不一定很複雜,並且總是可以對任何顯著影響提出合理的解釋。特別是在沒有特定預測的情況下。然而一個人的分析流程中的變化越多,觀察到的效果不真實的可能性就越大。當同一個社區報告相同的結果變數但在論文中以不同方式計算該變數的數值時(例如www.flexiblemeasures.com;
Carp, 2012; Francis, 2013)或臨床試驗轉換時,數據分析的靈活性尤其明顯他們的成果(Altman
等, 2017;
Goldacre等,
2019)。
這個問題可以通過使用標準化分析方法、設計和分析的預註冊(Nosek
& Lakens, 2014)或進行複制研究(Button
等, 2013)來預先解決。請注意,可以在第一次實驗的結果已知之後以及在尋求該效果的內部複製之前執行實驗的預註冊。但也許防止
p-hacking
的最佳方法是對臨界或非顯著結果表現出一定的容忍度。換句話說如果實驗設計、執行和分析得當,審稿人就不應該因為他們的數據而“懲罰”研究人員。
如何檢測它
分析的靈活性很難檢測,因為研究人員很少披露所有必要的資訊。在預註冊或臨床試驗註冊的情況下,審查者應將執行的分析與計劃的分析進行比較。在沒有預先註冊的情況下,幾乎不可能檢測到某些形式的
p-hacking。然而,審稿人可以估計所有的分析選擇是否合理,是否在以前的出版物中使用了相同的分析計劃,研究人員是否提出了一個有問題的新變數,或者他們是否收集了大量的量測結果並只報告了幾個重要的。
Forstmeier等(2017)總結了檢測可能的陽性結果的實用技巧。
研究人員解決方案
研究人員在報告結果時應保持透明,例如區分預先計劃與探索性分析以及預測與意外結果。正如我們在下面討論的那樣,使用靈活數據分析的探索性分析是很好的,如果它們以透明的方式報告和解釋,特別是如果它們作為預先指定分析的複制的基礎(Curran-Everett
& Milgrom, 2013)。這樣的分析可以成為進一步研究的有價值的理由,但不能成為強有力的結論的基礎。
8.未能糾正多重比較
問題
當研究人員探索任務效果時,他們通常會探索多個任務條件對多個變數(行為結果、問卷項目等)的影響,有時會使用未確定的先驗假設。這種做法被稱為探索性分析,而不是確認性分析。根據定義,驗證性分析更具限制性。當使用頻率統計進行時,在探索性分析期間進行多重比較可能會對重要發現的解釋產生深遠的影響。在涉及兩個以上條件(或兩組比較)的任何實驗設計中,探索性分析將涉及多重比較,並且即使不存在這種影響(假陽性,I
型錯誤),也會增加檢測到影響的概率。在這種情況下因子的數量越多,可以執行的測試數量就越多。結果觀察到假陽性的概率增加(家庭錯誤率)。例如,在
2 × 3 × 3 的實驗設計中,發現至少一個顯著的主效應或交互作用的概率為 30%,即使沒有效應也是如此(Cramer
等, 2016)。
在進行多重獨立比較(例如神經影像分析、多個記錄的細胞或腦電圖)時,這個問題尤為突出。在這種情況下,研究人員在技術上在每個體素/細胞/時間點內部署統計測試,從而增加了檢測到假陽性結果的可能性。因為設計中包含了大量措施。例如Bennett
和他的同事 (
Bennett et
al., 2009)在沒有進行多重比較校正時,在一條死去的大西洋鮭魚中發現了大量活躍的體素(在“心理化”任務期間被激活)。這個例子展示了識別虛假的重要結果是多麼容易。雖然當分析是探索性的時問題更大,但當大量分析被預先指定用於驗證性分析時,它仍然可能是一個問題。
如何檢測它
通過解決量測的自變數數量和執行分析的數量,可以檢測到未能糾正多重比較。如果這些變數中只有一個與因變數相關,那麼其餘變數可能已被包括在內,以增加獲得顯著結果的機會。因此在使用大量變數(例如基因或
MRI
體素)進行探索性分析時,研究人員在沒有明確理由的情況下解釋沒有經過多重比較校正的結果是完全不可接受的。即使研究人員提供了一個粗略的預測(例如,應該在特定的大腦區域或近似潛伏期觀察到效果),如果該預測可以通過多次獨立比較進行測試,則需要對多次比較進行校正。
研究人員解決方案
探索性測試可能是絕對合適的,但應該得到承認。研究人員應披露所有量測變數並正確實施多重比較程序的使用。例如,對多重比較應用標準校正不出所料地導致死魚示例中沒有活動體素(Bennett
等, 2009)。請記住,有很多方法可以糾正多重比較,有些方法比其他方法更容易被接受(Eklund等,
2016),因此僅僅存在某種形式的校正可能是不夠的。
9.過度解讀不顯著的結果
問題
當使用頻率統計時,科學家應用統計臨界值(通常
alpha=.05)來判斷統計顯著性。關於這個臨界值的任意性已經發表很多文章(Wasserstein
等, 2019),並且已經提出了替代方案(例如,Colquhoun,2014;
Lakens等,
2018;
Benjamin
等, 2018)。除了我們在最後的評論中詳細闡述的這些問題之外,當結果不顯著時,誤解統計測試的結果也是非常有問題的,但非常普遍。這是因為非顯著性
p
值無法區分是由於客觀上不存在效果(與假設相矛盾的證據),或由於數據不敏感而導致研究人員無法嚴格評估預測。例如,由於缺乏統計能力、不適當的實驗設計等。簡而言之,不顯著的效果實際上可能代表著非常不同的東西
,真正的無效結果,動力不足的真實效果或模棱兩可的效果(參見Altman
& Bland, 1995的示例)。因此如果研究人員希望將不顯著的結果解釋為反對假設的支持證據,他們需要證明該證據是有意義的。
p 值本身不足以達到此目的。這種混淆也代表著有時研究人員可能會忽略不符合 p≤0.05
臨界值的結果,假設它實際上是沒有意義的,而事實上它提供了足夠的證據來反對該假設,或者至少是需要進一步關注的初步證據。
如何檢測它
研究人員可能會將不顯著的 p
值解釋或描述為表明不存在影響。此錯誤非常常見,應突出顯示為有問題的。
研究人員解決方案
重要的第一步是報告效應大小和
p 值,以提供有關效應大小的資訊(Sullivan
& Feinn, 2012)。這對於任何未來的巨量分析也很重要(Lakens,
2013;
Weissgerber等,
2018)。例如,如果在大樣本量研究中的非顯著效應量級也非常小,則它在理論上不太可能有意義。而具有中等效應量的研究可能需要進一步研究(Fethney,
2010)。如果可能,研究人員應考慮使用能夠區分證據不足(或模棱兩可)和支持零假設的證據的統計方法(例如貝葉斯統計;
(Dienes, 2014
) 或等價檢驗 ( Lakens, 2017)。或者,研究人員可能已經先驗地確定他們是否有足夠的統計能力來識別所需的效果,或者確定這種先驗效果的信賴區間是否包含零值(Dienes,
2014)。否則研究人員不應過度解釋不顯著的結果,而僅將其描述為不顯著。
10 .相關性和因果關係
問題
這可能是解釋統計結果時最古老和最常見的錯誤(例如,參見Schellenberg,
2019)。在科學中,相關性通常用於探索兩個變數之間的關係。當發現兩個變數顯著相關時,通常很容易假設一個變數導致另一個變數。然而這是不正確的。僅僅因為兩個變數的可變性似乎線性地同時發生並不一定代表著它們之間存在因果關係,即使這種關聯是合理的。例如不同國家每年巧克力消費量與諾貝爾獎獲得者人數之間存在顯著相關性(r(20)=.79;
p<0.001),這導致了不正確的建議,即巧克力攝入量為諾貝爾獎獲得者提供了營養基礎(Maurage等,
2013)。僅相關性不能用作因果關係的證據。相關事件可能反映直接或反向因果關係,但也可能是由於未知共同原因,或者它們可能是簡單巧合的結果。
如何檢測它
每當研究人員報告兩個或多個變數之間的關聯不是由於操縱並使用因果關係時,它們很可能會混淆相關性和因果關係。研究人員只應在精確操縱變數時使用因果關係,即便如此,他們也應謹慎對待第三變數或混雜因素的作用。
研究人員解決方案
如果可能,研究人員應嘗試探索與第三個變數的關係,以進一步支持他們的解釋。例如使用分層建模或中介分析(但前提是他們有足夠的能力),通過測試競爭模型或直接操縱變數對隨機對照試驗感興趣(Pearl,
2009)。否則當證據具有相關性時,應避免使用因果關係。
最後的評論
避免這十個推理錯誤是確保結果不會被嚴重誤解的重要第一步。然而這個列表的一個關鍵假設是顯著性檢驗(如 p
值所示)對科學推論有意義。特別是,除了少數項目(參見“缺乏適當的控制條件/組”和“相關性和因果關係”)外,我們提出的大多數問題以及我們提供的解決方案都與
p-值,以及與給定統計檢驗相關的 p
值代表其實際錯誤率的概念。目前關於無效假設顯著性檢驗的有效性和顯著性臨界值的使用一直存在爭議(Wasserstein等,
2019)。我們同意沒有單一的 p
值可以揭示關聯或效果的合理性、存在性、真實性或重要性。然而,禁止 p
值並不一定能保護研究人員免於對其發現做出錯誤推斷(Fricker等,
2019)。如果以負責任的方式應用(Kmetz,
2019;
Krueger &
Heck, 2019;
Lakens, 2019),p
值可以提供對結果的有價值的描述,目前可以幫助科學交流(Calin-Jageman
& Cumming, 2019),至少直到建立解釋統計效應的新共識。我們希望這篇論文能幫助作者和審稿人解決其中一些主流問題。 |