|
資料來源:
Statistical notes for clinical researchers: Understanding standard
deviations and standard errors
Hae-Young
Kim
Restor
Dent Endod . 2013 Nov;38(4):263-5.
http://dx.doi.org/10.5395/rde.2013.38.4.263
標準誤差和標準偏差之間的區別並不容易解釋。令人困惑的是,標準誤差本身就是一種標準偏差。但是,標準偏差和標準誤差之間的根本區別在於,前者用於描述(descriptive)目的,而後者用於推理(inference)過程,關於樣本的資訊用於對總體母群進行解釋。
標準偏差
標準偏差(通常縮寫為 SD)顯示數據中與平均值存在的多少變化或偏差。與平均值或“偏差”的距離是通過從每個觀察值中減去平均值來獲得的。所得偏差具有正號或負號。由於平均偏差值總是為零,偏差值平方以獲得正數。平方偏差的平均和,通常稱為方差,通過使用平方根轉換為原始單位。它表示為
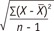 ,在數據樣本中;其中
n 是觀察次數。 ,在數據樣本中;其中
n 是觀察次數。
因此,標準偏差大致代表從平均值到觀測值的平均距離。在常態分佈的數據中,預計
95% 的觀測值在X ± 2(或
1.96)*SD 的範圍內。
從樣本到總體母群的橋樑:抽樣分佈
基本上,“統計”原理假設我們將樣本作為相應總體母群的一部分進行調查。利用樣本資訊獲取總體母群資訊,此統計推斷是“統計學”學科的核心內容。術語“統計”是指從樣本計算的任何值,例如樣本平均值、中位數、眾數、比例、相關係數。
當我們嘗試使用樣本獲取總體母群資訊時,我們不可避免地會選擇不同的樣本集。假設我們選擇樣本大小為 2,這代表著有兩個觀察值,來自原具有五個元素的總體母群,例如
1、2、3、4
和 5。我們可以選擇 25
組不同的樣本 (1,1),( 1,2),
(1,3)...(2,1),...(5,3), (5,4), (5,5) 並獲得 9
個不同的樣本平均值,其中 1, 1.5、2、2.5、3、3.5、4、4.5
和 5。這個概念來自是我們可以選擇許多不同的樣本集,這稱為“樣本變異性”。我們總是需要考慮由許多不同的可能樣本集,引起的樣本變異性,因為我們只是調查總體母群一部分樣本,來針對目標總體母群做出一些陳述。
由於樣本的可變性,我們可以考慮不同統計值的分佈,例如不同的樣本平均值。樣本統計量的所有可能值(例如來自相同大小樣本的樣本平均值)的分佈稱為“抽樣分佈”。如果分佈近似常態,我們可以預期抽樣分佈的平均值與真實總體母群值相同。標準誤差是抽樣分佈的標準偏差。圖
1描述了不同樣本的選擇,顯示了樣本的可變性並導致樣本平均值的抽樣分佈。抽樣分佈是一個重要的概念,因為它將樣本中觀察到的樣本統計量,與相應總體母群中的真實值聯繫起來。
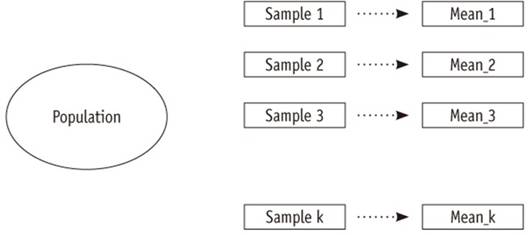
圖1不同樣品的選擇和樣品的變異性。
標準誤差
1.
什麼是標準誤差?
如上所述,標準誤差被定義為“統計抽樣分佈的標準偏差”。標準誤差的大小通常在很大程度上取決於樣本的大小。樣本平均值的標準誤差表示為標準偏差/√樣本大小。小標準偏差和大樣本數量可能導致樣本平均值的小標準誤差。
SE平均值=
SD / √ n
當標準偏差很大時,我們知道與平均值和單數值的平均距離很大,因此數值的分佈範圍很廣。一個大的標準誤差怎麼辦?與標準差的情況類似,大的標準誤差代表著抽樣分佈廣泛,從平均值到抽樣分佈中某個數值的平均距離較大。在樣本平均值的抽樣分佈中,找到距平均值較遠的觀測值有什麼相關性?因為真實總體母群值是樣本平均值的抽樣分佈的平均值,所以與平均值的距離可用於推斷在找到真實總體母群平均值時可能不正確的程度。換句話說,標準誤差的大小可以表明樣本平均值與真實總體母群值的平均距離。因此,較小的標準誤差可能代表著我獲得的樣本平均值而言可能更接近真實總體母群平均值,並且犯大量錯誤的機會更小。在調查樣本時,我們的目標是盡可能接近真實總體母群值。因此,與總體母群值有很大差異(或稱為誤差)的估計值將令人失望。這就是為什麼將抽樣分佈的標準差稱為標準誤差的原因。
2.
標準誤差在統計推論中的重要性
標準誤差在評估樣本統計數據以確定真實總體母群值方面有著非常重要的作用。我們在計算信賴區間時使用標準誤差。對於大樣本,總體母群平均值的
95% 信賴區間計算,為從(樣本平均值
-1.96 * SE) 到(樣本平均值
+1.96 * SE )的區間,這代表著該區間將以 95%
的確定性包含真實總體母群平均值。如果得到的樣本平均值位於與真值比較接近的 95%
中,並且不在抽樣分佈中遠離真值的 5%
中,則計算的信賴區間應包括母群價值。如果標準誤差足夠小,並且得到的 95%
信賴區間足夠窄,則可以足夠精確地估計總體母群值。
同樣在估計的顯著性檢驗中,估計的標準誤差具有決定性作用。當我們決定總體母群平均值是否為我們的假設平均值時,我們會將數值轉換為標準化分佈,例如
z 或 t
分佈。這種轉換是通過觀察平均值和假設值之間的差異,再除以平均值的標準誤差來完成的。
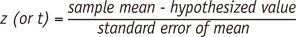
如果樣本平均值以標準誤差為單位遠離假設值,則
z 或 t 的絕對值會很大。當計算的 z
或 t 值大於指定的臨界值(例如
1.96)時,我們得出結論,觀察結果與假設存在顯著差異。因此,重要的不是樣本平均值本身的大小,而是樣本平均值與標準誤差的比率。如果標準誤差很大,例如
100,000 並且假設值為零,即使樣本平均值為 10,000,z
或 t 的標準化值也僅為 0.1,這表示總體母群值可能為零,而樣本平均值
10,000
不是與假設值零有顯著不同。因此,當您看到任何估計值時,在您檢查估計值的標準誤差的大小之前,您不能認為數值大小是小或大。在評估從樣本計算的所有類型的統計數據時,應採用相同的原則,例如平均值差、比例、相關係數或迴歸係數。圖
2顯示了上述三種不同的分佈。
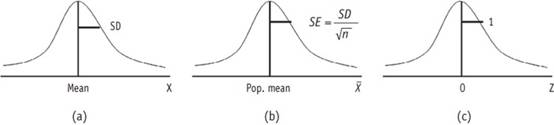
圖 2
三種不同的分佈。 (a)
總體母群或樣本的分佈; (b) 樣本平均值的抽樣分佈;
(c) 標準化正常; (Z) 分佈。 |