|
資料來源:
Standard deviation
and standard error of the mean
Dong Kyu Lee,1 Junyong
In,2 and Sangseok
Lee3
Korean J Anesthesiol. 2015
Jun; 68(3): 220–223.
Published online
2015 May 28. doi: 10.4097/kjae.2015.68.3.220
摘要
在大多數臨床和實驗研究中,標準偏差 (SD) 和平均值估計標準誤差 (SEM)
用於表現樣本數據的特0,徵並解釋統計分析結果。然而一些作者偶爾會混淆醫學文獻中 SD 和 SEM 之間的獨特用法。由於SD 和 SEM
的計算過程中包含不同的統計推論,它們中的每一個都有自己的含義。 SD 是數據在常態分佈中的離散度。換句話說,SD
表示以平均值代表樣本數據的準確程度。然而,SEM 的含義包括基於抽樣分佈的統計推論。 SEM 是樣本平均值的理論分佈(抽樣分佈)的 SD。雖然
SD 或 SEM 都可用於描述數據和統計結果,但應了解使用 SD 和 SEM 的合理方法。此文目的在說明 SD 和 SEM
之間的區別,並為兩者提供適當的使用指南,總結數據並描述統計結果。
當數據的值均勻地分佈在一個代表值周圍時,就稱該數據服從常態分佈。常態分佈是參數統計分析的先決條件 [1
]。常態分佈數據中的平均值表示數據值的集中趨勢。然而當試圖解釋分佈的形狀時,僅靠平均值是不夠的。因此,許多醫學文獻採用標準偏差 (SD)
和平均值的標準誤差 (SEM) 以及平均值來報告統計分析結果 [2]。
本文的目的是說明 SD 和 SEM
在常態分佈數據的描述性,和統計分析中使用的差異,並提出一個標準,可以根據該標準評估醫學文獻中的統計分析結果.
醫學研究首先建立關於母群的假設並從母群中提取樣本來檢驗假設。如果抽樣過程是通過適當的隨機化方法和足夠的樣本量進行的,則提取的樣本將呈常態分佈。與所有常態分佈的數據一樣,樣本的特徵由平均值、變異數或
SD 表示。變異數或 SD 包括觀測值與平均值的差異(圖 1);因此,這些值表示數據 [1-3]
的變化。例如,如果觀測值在平均值周圍分散緊密,則變異數以及 SD
都會減小。但是,變異數可能會混淆數據的解釋,因為它是通過對觀察值的單位進行平方和計算得出的。因此使用與平均值相同的單位的 SD 更合適 [
3 ](公式
1 和 2)。
樣品:x1, x2, x3 ,..., xn (樣本大小 = n)
平均值( x̄ ) = ∑xi /n
變異數= ∑ (x̄−xi )2/(n −1),
標準偏差(SD)=√變異數
Standard
deviation and standard error of the mean
Dong Kyu Lee, 1 Junyong
In,2 and Sangseok
Lee3 1 Junyong
In,2 and Sangseok
Lee3
Korean J Anesthesiol. 2015
Jun; 68(3): 220–223.
Published
online 2015 May 28. doi: 10.4097/kjae.2015.68.3.220
摘要
在大多數臨床和實驗研究中,標準偏差 (SD) 和平均值估計標準誤差
(SEM) 用於表現樣本數據的特0,徵並解釋統計分析結果。然而一些作者偶爾會混淆醫學文獻中 SD 和 SEM 之間的獨特用法。由於SD 和
SEM 的計算過程中包含不同的統計推論,它們中的每一個都有自己的含義。 SD 是數據在常態分佈中的離散度。換句話說,SD
表示以平均值代表樣本數據的準確程度。然而,SEM 的含義包括基於抽樣分佈的統計推論。 SEM 是樣本平均值的理論分佈(抽樣分佈)的 SD。雖然
SD 或 SEM 都可用於描述數據和統計結果,但應了解使用 SD 和 SEM 的合理方法。此文目的在說明 SD 和 SEM
之間的區別,並為兩者提供適當的使用指南,總結數據並描述統計結果。
當數據的值均勻地分佈在一個代表值周圍時,就稱該數據服從常態分佈。常態分佈是參數統計分析的先決條件 [1
]。常態分佈數據中的平均值表示數據值的集中趨勢。然而當試圖解釋分佈的形狀時,僅靠平均值是不夠的。因此,許多醫學文獻採用標準偏差 (SD)
和平均值的標準誤差 (SEM) 以及平均值來報告統計分析結果 [2]。
本文的目的是說明 SD 和 SEM
在常態分佈數據的描述性,和統計分析中使用的差異,並提出一個標準,可以根據該標準評估醫學文獻中的統計分析結果.
醫學研究首先建立關於母群的假設並從母群中提取樣本來檢驗假設。如果抽樣過程是通過適當的隨機化方法和足夠的樣本量進行的,則提取的樣本將呈常態分佈。與所有常態分佈的數據一樣,樣本的特徵由平均值、變異數或
SD 表示。變異數或 SD 包括觀測值與平均值的差異(圖 1);因此,這些值表示數據 [1-3]
的變化。例如,如果觀測值在平均值周圍分散緊密,則變異數以及 SD
都會減小。但是,變異數可能會混淆數據的解釋,因為它是通過對觀察值的單位進行平方和計算得出的。因此使用與平均值相同的單位的 SD 更合適 [
3
](公式 1 和 2)。
樣品:x1, x2, x3 ,..., xn (樣本大小 = n)
平均值( x̄ ) = ∑xi /n
變異數= ∑ (x̄−xi
)2/(n −1),
標準偏差(SD)=√變異數
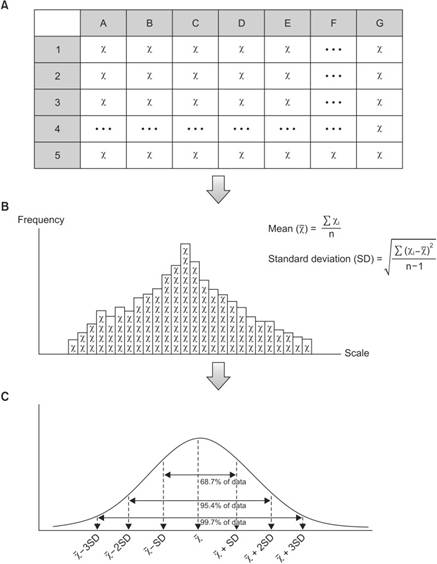
圖.1
描述數據的過程。首先,我們通過隨機化(A)從母群中收集原始數據。然後我們根據尺度(頻率分佈)排列每個值;我們可以假設分佈的形狀(概率分佈)並且可以計算平均值和標準偏差(B)。使用這些平均值和標準偏差,我們生成了一個常態分佈模型
(C)。該分佈代表了我們收集的數據的特徵,是常態分佈,可以進行統計推論(χ̅:平均值,SD:標準偏差, χi
:觀察值,n:樣本量)。
如前所述,將 SD
與平均值同時使用,可以更準確地估計常態分佈數據的變化。換句話說,可以通過檢查數據[
1
]的平均值和 SD(圖
1 ),來實現常態分佈的統計模型。在此類模型中,大約 68.7% 的觀測值位於距平均值 1 個標準偏差範圍內,大約
95.4% 的觀測值位於距平均值兩個標準偏差以內,大約 99.7% 的觀測值位於距平均值 3 個標準偏差範圍內[
1 ,
4
]。出於這個原因,大多數醫學文獻以平均值和標準偏差的形式報告他們的樣本 [
5
]。
醫學文獻中提到的樣本是一組來自母群的觀察值。必須對整個母群進行實驗才能更準確地確認假設,但基本上不可能調查整個母群。因此以適當的抽樣過程(提取代表總體母群特徵其樣本的過程)對於獲得可靠結果十分重要。為此,在研究計劃階段確定適當的樣本數量,並通過隨機化方法進行抽樣。儘管如此,提取的樣本仍然是總體母群的一部分。因此,樣本平均值是總體母群平均值的估計值。當從同一總體母群中重複隨機抽取相同樣本量的樣本時,由於樣本變異和樣本平均值,它們彼此不同(圖2,B級)。通過重複抽樣過程,實現的不同樣本平均值的分佈稱為抽樣分佈,它為常態分佈模式(圖2,C級)
[
1,6,7 ]
。因此可以計算抽樣分佈的 SD;這個值被稱為 SEM [
1 ,
6 ,
7
]。 SEM 取決於總體母群的變化和提取樣本的數量。總體母群的變化量較大會導致樣本平均值的較大差異,最終導致較大的 SEM。但是隨著從總體母群中提取更多樣本,樣本平均值會更接近總體母群平均值,從而導致
SEM 更小。簡而言之,SEM 是樣本平均值與總體母群平均值的接近程度的指標 [
7
]。然而在實際上,僅從總體母群中提取了一個樣本。因此,使用 SD 和样本大小 (Estimated SEM) 估計 SEM。由統計程序計算的
SEM ,是通過此過程計算的估計值 [
5
]。
平均值的估計標準誤差 (SEM )= SD / √n

圖 2統計推論的過程。 A
級表示母群。在大多數實驗中,我們僅使用隨機化從總體母群中獲得一組樣本數據(B
級);平均值和標準偏差是根據我們有的樣本數據計算得出的。出於統計推論的目的,我們假設總體母群中有幾個樣本數據集(B
級);每個樣本數據集的平均值產生抽樣分佈(C 級)。使用這種抽樣分佈,可以進行統計分析。在這種情況下,平均值或 95%
信賴區間的估計標準誤差,在統計分析過程中具有重要作用(χ̅:平均值,SD:標準偏差,n:樣本量,N:從母群取樣的樣本數據)。
設置信賴區間以直觀地說明總體母群平均值。 95%
的信賴區間是最常見的 [
3 ,
7
]。抽樣分佈的 SEM 由一個樣本估計值,信賴區間由 SEM 確定(圖
2 ,C 級)。嚴格意義上,95% 信賴區間提供了有關 95% 樣本平均值將落入的範圍的,它不見得是具有 95%
信賴度的總體母群平均值的範圍。例如,95% 的信賴區間表示當從總體母群中的 100 個樣本計算 100 個樣本平均值時,其中 95
個包含在所述信賴區間內,5 個位於信賴區間之外。換句話說,這並不代表著總體母群平均值有 95% 的概率位於95% 的信賴區間內。
在對於數據集進行統計比較時,研究人員會估計每個樣本的總體母群並檢查它們是否相同。 SEM,而不是代表樣本變化的 SD,用於估計總體母群平均值(圖2
)( 4、8、9
]
。通過這個過程,研究人員得出結論,他們研究中使用的樣本恰當地代表了預設顯著性水準 [
4 ,
6 ,
8 ]
指定的誤差範圍內的總體母群。
SEM 小於 SD,因為 SEM 通常估計為 SD
除以樣本大小的平方根。由於這個原因,研究人員在描述他們的樣本時很想使用 SEM。如果兩組的樣本量相等,則可以使用 SEM 或 SD
來比較兩個不同的數據組。但是,為了提供準確的資訊,必須說明樣本數量。例如,當一個總體母群有大量變異時,從該總體母群中提取的樣本的 SD
必須很大。但是,如果故意增加樣本量,則 SEM 會變小。在這種情況下,很容易在描述性統計中使用 SEM
來誤解總體母群。這種情況在醫學研究中很常見,因為醫學研究中的變數施加了許多可能的偏差,這些偏差源於個體間和個體內部的差異,這些差異源於患者的潛在一般狀況等。然而,在解釋
SD 和 SEM 時,應考慮 SD 和 SEM 的確切含義和目的,以提供正確的資訊。 [
3、4、6、7、10 ]
。
我們檢查了發表在《韓國麻醉學雜誌》第 6
卷第1至第6期的36項臨床或實驗研究,發現其中一些研究不恰當地使用了 SD 和 SEM。首先檢查描述性統計數據,我們發現所有研究都使用平均值和
SD 或觀察到的數量和百分比。一項研究提出了 95%
的信賴區間;這項特定的研究適當地說明了信賴區間內的樣本量,從而更清楚地了解了研究中建議的數據 [
11
]。在檢查的 36 項研究中,只有一項研究描述了常態性檢驗的結果 [
12
]。其次,所有 36 項研究都使用
SD、觀察到的數量或百分比來描述他們的統計結果。有一項研究沒有具體說明圖表中的值代表什麼(即是平均值、或是標準偏差或四分位距)。還有一項研究在文本中使用了平均值,但在圖表中顯示了四分位數範圍。
16 項研究使用觀察到的數字或百分比,其中大多數報告的結果沒有信賴區間。只有兩項研究說明了信賴區間,但這兩項研究中只有一項適當地使用了信賴區間
[
13
]。如上所示,我們發現一些研究在報告其統計結果時不恰當地使用了 SD、SEM
和信賴區間。在稿件審查和評估期間,必須仔細篩選此類不恰當使用統計數據的實例,因為它們可能會妨礙對研究數據的準確理解。
總之,SD反映了常態分佈數據的變化,而SEM代表了抽樣分佈的樣本平均值的變化。考慮到這一點,使用
SD(與常態性檢驗配對)來描述樣本的特徵是恰當的。但是,如果指定了樣本大小,則 SEM 或信賴區間可用於相同目的。 SEM
與樣本量相結合,在報告統計結果時更有用,因為它允許通過圖表或表格對估計的總體母群進行直觀的比較。
圖.1
描述數據的過程。首先,我們通過隨機化(A)從母群中收集原始數據。然後我們根據尺度(頻率分佈)排列每個值;我們可以假設分佈的形狀(概率分佈)並且可以計算平均值和標準偏差(B)。使用這些平均值和標準偏差,我們生成了一個常態分佈模型
(C)。該分佈代表了我們收集的數據的特徵,是常態分佈,可以進行統計推論(χ̅:平均值,SD:標準偏差, χi
:觀察值,n:樣本量)。
如前所述,將 SD
與平均值同時使用,可以更準確地估計常態分佈數據的變化。換句話說,可以通過檢查數據[
1
]的平均值和 SD(圖 1
),來實現常態分佈的統計模型。在此類模型中,大約 68.7% 的觀測值位於距平均值 1 個標準偏差範圍內,大約 95.4%
的觀測值位於距平均值兩個標準偏差以內,大約 99.7% 的觀測值位於距平均值 3 個標準偏差範圍內[
1 ,
4
]。出於這個原因,大多數醫學文獻以平均值和標準偏差的形式報告他們的樣本 [
5 ]。
醫學文獻中提到的樣本是一組來自母群的觀察值。必須對整個母群進行實驗才能更準確地確認假設,但基本上不可能調查整個母群。因此以適當的抽樣過程(提取代表總體母群特徵其樣本的過程)對於獲得可靠結果十分重要。為此,在研究計劃階段確定適當的樣本數量,並通過隨機化方法進行抽樣。儘管如此,提取的樣本仍然是總體母群的一部分。因此,樣本平均值是總體母群平均值的估計值。當從同一總體母群中重複隨機抽取相同樣本量的樣本時,由於樣本變異和樣本平均值,它們彼此不同(圖2,B級)。通過重複抽樣過程,實現的不同樣本平均值的分佈稱為抽樣分佈,它為常態分佈模式(圖2,C級)
[ 1,6,7 ]
。因此可以計算抽樣分佈的 SD;這個值被稱為 SEM [
1 ,
6 ,
7 ]。
SEM 取決於總體母群的變化和提取樣本的數量。總體母群的變化量較大會導致樣本平均值的較大差異,最終導致較大的 SEM。但是隨著從總體母群中提取更多樣本,樣本平均值會更接近總體母群平均值,從而導致
SEM 更小。簡而言之,SEM 是樣本平均值與總體母群平均值的接近程度的指標 [
7
]。然而在實際上,僅從總體母群中提取了一個樣本。因此,使用 SD 和样本大小 (Estimated SEM) 估計 SEM。由統計程序計算的
SEM ,是通過此過程計算的估計值 [
5 ]。
平均值的估計標準誤差 (SEM )= SD / √n
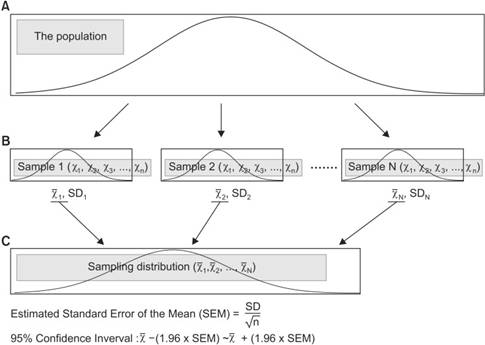
圖 2統計推論的過程。
A 級表示母群。在大多數實驗中,我們僅使用隨機化從總體母群中獲得一組樣本數據(B
級);平均值和標準偏差是根據我們有的樣本數據計算得出的。出於統計推論的目的,我們假設總體母群中有幾個樣本數據集(B
級);每個樣本數據集的平均值產生抽樣分佈(C 級)。使用這種抽樣分佈,可以進行統計分析。在這種情況下,平均值或 95%
信賴區間的估計標準誤差,在統計分析過程中具有重要作用(χ̅:平均值,SD:標準偏差,n:樣本量,N:從母群取樣的樣本數據)。
設置信賴區間以直觀地說明總體母群平均值。 95% 的信賴區間是最常見的 [
3 ,
7
]。抽樣分佈的 SEM 由一個樣本估計值,信賴區間由 SEM 確定(圖
2 ,C 級)。嚴格意義上,95% 信賴區間提供了有關 95% 樣本平均值將落入的範圍的,它不見得是具有 95%
信賴度的總體母群平均值的範圍。例如,95% 的信賴區間表示當從總體母群中的 100 個樣本計算 100 個樣本平均值時,其中 95
個包含在所述信賴區間內,5 個位於信賴區間之外。換句話說,這並不代表著總體母群平均值有 95% 的概率位於95% 的信賴區間內。
在對於數據集進行統計比較時,研究人員會估計每個樣本的總體母群並檢查它們是否相同。
SEM,而不是代表樣本變化的 SD,用於估計總體母群平均值(圖2
)( 4、8、9 ]
。通過這個過程,研究人員得出結論,他們研究中使用的樣本恰當地代表了預設顯著性水準 [
4 ,
6 ,
8 ]
指定的誤差範圍內的總體母群。
SEM 小於 SD,因為 SEM 通常估計為 SD
除以樣本大小的平方根。由於這個原因,研究人員在描述他們的樣本時很想使用 SEM。如果兩組的樣本量相等,則可以使用 SEM 或 SD
來比較兩個不同的數據組。但是,為了提供準確的資訊,必須說明樣本數量。例如,當一個總體母群有大量變異時,從該總體母群中提取的樣本的 SD
必須很大。但是,如果故意增加樣本量,則 SEM 會變小。在這種情況下,很容易在描述性統計中使用 SEM
來誤解總體母群。這種情況在醫學研究中很常見,因為醫學研究中的變數施加了許多可能的偏差,這些偏差源於個體間和個體內部的差異,這些差異源於患者的潛在一般狀況等。然而,在解釋
SD 和 SEM 時,應考慮 SD 和 SEM 的確切含義和目的,以提供正確的資訊。 [
3、4、6、7、10 ]
。
我們檢查了發表在《韓國麻醉學雜誌》第 6
卷第1至第6期的36項臨床或實驗研究,發現其中一些研究不恰當地使用了 SD 和 SEM。首先檢查描述性統計數據,我們發現所有研究都使用平均值和
SD 或觀察到的數量和百分比。一項研究提出了 95%
的信賴區間;這項特定的研究適當地說明了信賴區間內的樣本量,從而更清楚地了解了研究中建議的數據 [
11
]。在檢查的 36 項研究中,只有一項研究描述了常態性檢驗的結果 [
12
]。其次,所有 36 項研究都使用
SD、觀察到的數量或百分比來描述他們的統計結果。有一項研究沒有具體說明圖表中的值代表什麼(即是平均值、或是標準偏差或四分位距)。還有一項研究在文本中使用了平均值,但在圖表中顯示了四分位數範圍。
16 項研究使用觀察到的數字或百分比,其中大多數報告的結果沒有信賴區間。只有兩項研究說明了信賴區間,但這兩項研究中只有一項適當地使用了信賴區間
[ 13
]。如上所示,我們發現一些研究在報告其統計結果時不恰當地使用了 SD、SEM
和信賴區間。在稿件審查和評估期間,必須仔細篩選此類不恰當使用統計數據的實例,因為它們可能會妨礙對研究數據的準確理解。
總之,SD反映了常態分佈數據的變化,而SEM代表了抽樣分佈的樣本平均值的變化。考慮到這一點,使用
SD(與常態性檢驗配對)來描述樣本的特徵是恰當的。但是,如果指定了樣本大小,則 SEM 或信賴區間可用於相同目的。 SEM
與樣本量相結合,在報告統計結果時更有用,因為它允許通過圖表或表格對估計的總體母群進行直觀的比較。 |