中興大學 生物系統工程研究室 陳加忠

資料來源:

https://www.graphpad.com/guides/the-ultimate-guide-to-anova?utm_campaign=gp%20content&utm_medium=email&utm_content=226165817&utm_source=hs_email

ANOVA 是經典實驗設計的首選分析工具，它構成了科學研究的支柱。

在本文中，我們將指導您了解什麼是 ANOVA，如何確定使用哪個版本來評估您的特定實驗，並提供最常見形式的 ANOVA 的詳細示例。

這包括對交叉、巢式、固定和隨機因子的（簡要）討論，並涵蓋了科學家在需要統計學家或建模專家的幫助之前，會遇到的大多數 ANOVA 模型。

變異數分析用於什麼？

ANOVA 或（Fisher 的）變異數分析是一種關鍵的分析技術，用於評估實驗中三個或更多樣本平均值之間的差異。顧名思義，它根據一個或多個解釋因子劃分反應變數的變異數。

有多種類型的 ANOVA，例如單因子、雙因子和三因子 ANOVA 以及巢式和重複量測 ANOVA。下圖顯示了一個需要 ANOVA 的簡單實驗示例，研究人員在該實驗中量測了患有不同病毒性呼吸道感染的患者血漿中，中性粒細胞胞外陷阱 (neutrophil extracellular traps NET) 的水準。

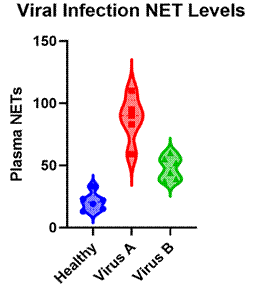
許多研究人員可能沒有意識到，對於大多數實驗，您運行的實驗的特徵決定了您需要用來測試結果的 ANOVA方法。雖然這是一個龐大的話題（一些高級技術需要專業訓練），但這是一本實用指南，涵蓋了大多數研究人員需要了解的關於 ANOVA 的知識。

我什麼時候應該使用變異數分析？

如果您的反應變數是數字，並且您正在尋找該數字在多個分類組中有何不同，那麼 ANOVA 是一個理想的起點。實驗運行後，ANOVA 用於分析這些分組因子中的一個或多個的平均反應之間是否存在差異。

ANOVA 可以處理多種實驗因子，例如對同一實驗單元的重複量測（例如，之前/期間/之後）。

如果您不想評估處理差異，而是想使用一組數值變數開發一個模型來預測該數值反應變數，請參閱線性迴歸和t 檢驗。

單因子、雙因子和三因子變異數分析有什麼區別？

ANOVA 中的“方式”數量（例如，單因子、雙因子……）就是您實驗中因子(factor)的數量。

儘管名稱上的差異聽起來微不足道，但 ANOVA 的複雜性隨著每個添加因子而大大增加。以農業為例，假設我們設計了一個實驗來研究不同因子如何影響作物的產量。

單因子實驗

在最基本的版本中，我們要評估三種不同的肥料。因為我們有兩個以上的組，所以我們必須使用 ANOVA。由於只有一個因子（肥料），因此這是單因子變異數分析。單因子變異數分析是最容易分析和理解的，但在作業中可能沒有那麼有用，因為只有一個因子是一個非常簡單的實驗。

當您添加第二個因子時會發生什麼？

如果我們有兩個不同的田區，我們可能想要添加第二個因子來查看該田區本身是否會影響成長。在每個田區中，我們都施用三種肥料（這仍然是主要興趣）。這稱為交叉設計。在這種情況下，我們有兩個因子，田區和肥料，並且需要雙因子ANOVA。

正如您可能想像的那樣，這使得解釋更加複雜，儘管仍然非常易於管理，因為涉及更多因子。現在有肥料效應和田區效應，並且可能存在相互作用效應，肥料在每個田區的表現不同。

添加第三個因子怎麼樣？

最後，變異數分析中可能有兩個以上的因子。在我們的示例中，也許您還想測試不同的灌溉系統。由於存在肥料、田區和灌溉因子，您可能會有三因子變異數分析。這大大增加了複雜性。

現在除了三個主要效應（肥料、田區和灌溉）之外，還有三個雙因子交互效應（田間施肥、灌溉施肥和田間灌溉）和一個三因子交互效應。

如果任何交互作用在統計上顯著，那麼呈現結果就會變得相當複雜。 “使用灌溉方法 C，肥料 A 在田區 B 上效果更好……”

在作業中，雙因子變異數分析通常與許多研究人員在諮詢統計學家之前想要得到的一樣複雜。話雖這麼說，三因子變異數分析很麻煩，但如果每個因子只有兩個水準時還是可以管理的。

什麼是交叉和巢式因子？

除了增加解釋的難度之外，具有多個因子的實驗（或由此產生的 ANOVA）增加了另一個複雜程度，即確定因子是交叉還是巢式。

對於交叉因子，每個因子之間的每個水準組合都會被觀察到。例如，每種肥料都施用於每個田區（因此在這種情況下，田區被細分為三個部分）。

使用巢式因子，一個因子的不同級別出現在另一個因子中。一個例子是向每個田區施用不同的肥料，例如向田區 1 施用肥料 A 和 B，向田區 2 施用肥料 C 和 D。

什麼是固定因子和隨機因子？

另一個具有兩個或多個因子的具有挑戰性的概念，是確定是否將這些因子視為固定因子或隨機因子。

當指定因子的所有水準（例如，化肥 A、化肥 B、化肥 C）並且您想要確定該因子對平均反應的影響時，使用固定因子。

當在大量或無限的可能數量（例如，所有田區）中僅觀察到某個因子的某些級別（例如，田區 1、田區 2、田區 3）時不能使用隨機因子，而是要觀察指定因子的影響，您無法做到這一點，因為您沒有觀察到所有可能的水準。以量化該因子內的可變性（每個田區中添加的可變性）。

許多關於 ANOVA 的入門課程只討論固定因子，除了兩個特定場景（巢式因子和重複量測）之外。

ANOVA 的實際假設是什麼？

這些是單因子變異數分析假設，但也適用於更複雜的雙因子或重複量測變異數分析。

1.分類處理或因子變數 - ANOVA 評估一個或多個分類變數（例如處理組）之間的平均差異，這些變數被稱為因子或“方式”。

2.三個或更多組 - ANOVA 中的所有因子必須至少有三個不同的組（或分類變數的水準）。可能性是無限的：三個不同組的一個因子，兩個組的兩個因子（2x2）等等。如果您的組少於三組，您可能可以通過簡單的 t 檢驗。

3.數值反應 - 雖然組是分類的，但在每個組中量測的數據（即反應變數）仍然需要是數值的。 ANOVA 從根本上說是一種用於量測組間數值反應差異的定量方法。如果您的反應變數不是連續的，那麼您需要一個更專業的建模方法，例如邏輯迴歸或卡方列聯表分析等等。

4.隨機分配 - 每個實驗組的組成應通過隨機選擇確定。

5常態性- 每個因子組合內的分佈應該近似常態。儘管由於中心極限定理導致樣本量增加，ANOVA 對這個假設相當穩健。

變異數分析的公式是什麼？

計算變異數分析的公式取決於因子的數量、關於因子如何影響模型的假設（及區劃分變數、固定或隨機效應、巢式因子等）以及觀察值之間的任何潛在重疊或相關性（例如，二次抽樣，重複量測）。

在 21 世紀運行 ANOVA 的好消息是，統計軟體可以處理大部分繁瑣的計算。研究人員需要做的主要事情是選擇適當的變異數分析。

雙因子交叉變異數分析的示例公式是：

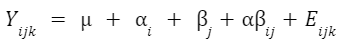
我怎麼知道要使用哪種變異數分析？

作為統計學家，我們希望您在進行實驗之前正在閱讀本文。通過將實驗簡化為標準格式以使分析簡單明了，您可以省去很多麻煩。

無論如何，我們將引導您為您的實驗選擇正確的變異數分析，並為最流行的案例提供示例。第一個問題是：

你只有一個感興趣的因子嗎？

如果您只量測了一個因子（例如，肥料 A、肥料 B 等），請使用單因子變異數分析。如果你有多個，那麼你需要考慮以下幾點：

您是否多次量測相同的觀察單位（例如，受試者）？

這是重複量測發揮作用的地方，對於研究人員來說可能是一個非常令人困惑的問題，但如果這聽起來像是描述您的實驗，請參閱重複量測變異數分析。否則：

是否有任何巢式因子，其中水準因另一個因子的水準而異？

在這種情況下，您有一個巢式的 ANOVA 設計。如果您沒有巢式因子或重複量測，那麼它變得簡單：

你有兩個分類因子嗎？

然後使用雙因子變異數分析。

你有三個分類因子嗎？

使用三因子變異數分析。

您是否記錄了非分類變數（例如年齡、體重等）？

儘管這些超出了本指南的範圍，但如果您有一個連續變數，則可以使用 ANCOVA，它允許連續共變數。對於多個連續共變數，您可能希望使用混合模型或可能的多元線性迴歸。

如何執行變異數分析？

一旦您確定哪種變異數分析適合您的實驗，請使用統計軟體運行計算。下面，我們提供一、二和三因子 ANOVA 模型的詳細示例。

如何閱讀和解釋 ANOVA 表？

解釋任何類型的 ANOVA 都應該從輸出中的 ANOVA 表開始。這些表就是 ANOVA 的名稱，因為它們將反應中的變異數劃分為各種因子和交互項。這是通過計算平方和 (SS) 和均方 (MS) 完成的，這可用於確定由每個因子解釋的反應中的變異數。

如果您已經預先確定了顯著性水準，則解釋主要歸結為來自 F 檢驗的 p 值。每個因子的原假設是該因子的組間沒有顯著差異。以下所有因子都具有統計顯著性，且 p 值非常小。

單因子變異數分析示例

單因子變異數分析的一個例子是培養皿中的細胞生長實驗。反應變數是對其生長的度量，而感興趣的變數是處理，它具有三個水準：公式A 、公式 B 和控制。

經典的單因子變異數分析假設每個樣本組內的變異數相等。如果這對您的數據來說不是一個有效的假設，那麼您有很多選擇。

計算單因子變異數分析

使用 Prism 進行分析，我們將運行單因子變異數分析，並選擇 95% 作為我們的顯著性臨界值。由於我們對三個組之間的差異感興趣，我們將評估每個組並進行多重比較。

對於以下內容，我們將假設處理組內的變異數相等。

要查看的第一個測試是整體（或綜合）F 檢驗，虛無假設是任何處理組之間沒有顯著差異。在這種情況下，三組之間存在顯著差異（p<0.0001），這告訴我們至少其中一組具有統計學上的顯著差異。

現在我們可以轉移到問題的核心，即確定哪些組的平均值在統計上是不同的。要了解更多資訊，我們應該繪製數據圖表並測試差異（使用多重比較校正）。

繪製單因子變異數分析

可視化變異數分析結果的最簡單方法是使用顯示所有單個點的簡單圖表。最好使用顯示每個組的所有數據點和平均值的圖，例如散點圖或小提琴圖，而不是條形圖。

例如，您可以在下圖看到每個處理組中每個數據點的細胞生長水準圖表，以及表示它們平均值的線。這可以幫助確認發現的任何顯著差異，並顯示組\重疊的緊密程度。

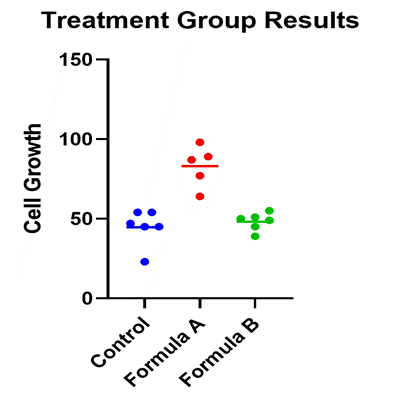
確定組間的統計顯著性

除了圖形，我們真正想知道的是哪些處理手段在統計上是不同的。因為我們正在執行多個測試，所以我們將使用多重比較校正。對於我們的示例，我們將使用 Tukey 的校正（如果我們只對每個處理與控制組之間的差異感興趣，我們可以使用Dunnett 的校正）。

在這種情況下，配方 A 的平均細胞生長顯著高於對照 (p<.0001) 和配方 B (p=0.002)，但配方 B 和對照之間沒有顯著差異。

雙因子變異數分析示例

對於雙因子 ANOVA，涉及兩個因子。我們的例子將集中在一個細胞系的例子上。假設我們有一個 2x2 設計（總共四個分組）。有兩種不同的處理方法（血清飢餓和正常培養）和兩個不同的田區。總共有19個細胞系“實驗單元”正在評估，每組最多5個（請注意，有4個組和19個觀察單元，本研究不平衡）。雖然每組中有多個單元，但它們都是完全不同的重複，因此不是對同一單元的重複量測。

與單因子變異數分析一樣，繪製數據圖表並查看變異數分析表以獲取結果是一個好主意。

繪製二維變異數分析

這裡有很多選擇。就像我們的單因子示例一樣，我們推荐一種類似的繪圖方法，該方法顯示所有數據點本身以及平均值。

在雙因子變異數分析中確定組間的統計顯著性

讓我們使用具有 95% 顯著性臨界值的雙因子 ANOVA 來評估這兩個因子對反應的影響，反應是一種衡量生長的方法。

您可以根據需要隨時使用的雙因子 ANOVA 檢查表進行自己的分析。

首先，請注意模型中包含三個變異來源，它們是交互作用、處理和田區。

要查看的第一個效應是交互項，因為如果它很重要，它會改變您解釋主要效應的方式（例如，處理和田區）。交互效應計算一個因子的影響是否取決於另一個因子。在這種情況下，顯著交互項 (p<.0001) 表明處理效果取決於田區類型。

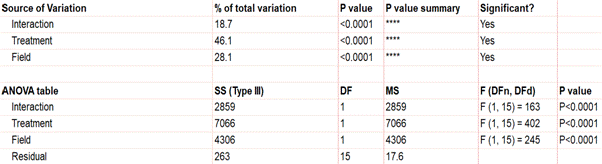
一個重要的交互項混淆了解釋，因此您不再有“處理 A 優於處理 B”的簡單結論。在這種情況下，圖形特別有用。這表明雖然三組之間可能存在一些差異，但在田區 2 中飢餓血清的精確組合優於其他組。

為了確認是否存在統計學上顯著的結果，我們將進行成對比較（將每個因子水準組合與其他因子水準組合進行比較）並考慮多重比較。

我是否需要糾正(correct)雙因子 ANOVA 的多重比較？

如果您要比較多個處理組組合的平均值，那麼絕對可以！這是有關雙因子 ANOVA 多重比較的更多資訊。

重複量測變異數分析

到目前為止，我們幾乎只關注“普通”變異數分析及其差異，具體取決於涉及多少因子。在所有這些情況下，每個觀察都與其他觀察完全無關。除了重複中可能相同的因子組合之外，每個重複本身都是獨立的。

ANOVA 的第二個常見分支稱為重複量測。在這些情況下，單位是相關的，因為它們以某種方式匹配。重複量測用於模擬個體或受試者內量測之間的相關性。當個體內部的變異性相對於個體之間的變異性較大時，重複量測變異數分析是有用的並增加了統計檢定力。

重要的是，您的重複量測因子（通常是時間）的所有級別都是一致的。如果不是，您將需要考慮運行混合模型，這是一種更高級的統計技術。

重複量測有兩種常見形式：

1.你在不同的時間點觀察同一個人或樣本。如果您熟悉配對 t 檢驗，這是對它的擴展。（您也可以讓同一個人接受所有處理，這增加了另一個級別的重複措施。）

2.您有一個隨機區組設計，其中匹配的元素接受每種處理。例如，您將從一個人身上採集的大量血液樣本分成 3 個（或更多）較小的樣本，每個較小的樣本都只接受一次處理。

重複量測變異數分析可以有任意數量的因子。

用重複量測變異數分析假設球形(Sphericity)是什麼意思？

重複量測幾乎總是被視為隨機因子，這代表著需要定義重複量測水準之間的相關結構。球形假設代表著假設重複量測的每個級別與每個其他級別具有相同的相關性。

隨著時間的推移重複量測（例如基線、處理時、處理後 1 小時）幾乎不會出現這種情況，在這些情況下，我們建議不要假設球形度。但是，如果您使用隨機區組設計，那麼球形度通常是合適的。

具有重複量測的示例雙因子 ANOVA

假設我們有兩種處理方法（對照和處理）來使用測試動物進行評估。我們將對每兩隻動物（複製）進行兩種處理，並在兩次處理之間留出足夠的時間，這樣就不會產生交叉或遺留效應。此外，我們將量測每種處理的五個不同時間點（基線、注射時、一小時後……）。這是重複量測，因為我們需要在每次處理下量測來自同一動物的匹配樣本，因為我們跟踪其刺激水準如何隨時間變化。

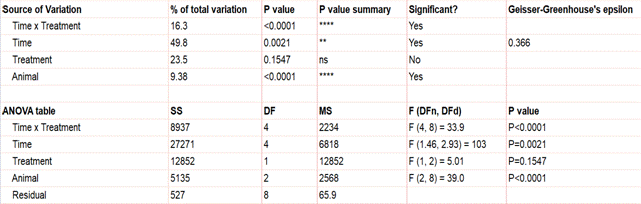
輸出顯示主效應和交互效應的測試結果。由於時間和處理之間的交互作用顯著（p<.0001），處理主效應不顯著（p=.154）這一事實並不值得注意。

繪製重複量測 ANOVA

正如我們一直在說的，繪製數據圖表很有用，當交互項很重要時尤其如此。在這裡，我們解釋了為什麼處理和時間之間的相互作用很重要，但處理本身並不重要。注射後一小時（以及之後的所有時間點），處理單元顯示出比對照更高的反應水準，即使它在這 12 小時內下降。因此，時間的效果取決於處理。在較早的時間點，處理和對照之間沒有區別。

繪製重複量測數據的圖形是一門藝術，但好的圖形可以幫助您理解和傳達結果。例如這是一個完全不同的實驗，但這是另一個重複量測實驗的精彩圖，其中包含在三種不同動物類型上量測的前後數值。

如果我有三個或更多因子怎麼辦？

解釋三個或更多因子非常具有挑戰性，通常需要高級訓練和經驗。

正如兩因子ANOVA 比單因子更複雜一樣，三因子 ANOVA 增加了更多混淆的可能性。您不僅要處理三個不同的因子，現在還要同時檢驗七個假設。這裡仍然存在雙因子交互，您甚至可能會遇到一個重要的三因子交互術語。

需要仔細規劃和先進的實驗設計才能解開將涉及的組合。

非參數變異數分析替代方案

與 t 檢驗或幾乎任何統計方法一樣，變異數分析也有替代方法來測試三組之間的差異。與 F 分佈相比，ANOVA 以平均值為中心並進行評估。

ANOVA 的兩個主要非參數表親是Kruskal -Wallis 和 Friedman 檢驗。正如 ANOVA 中的其他所有內容一樣，這兩個選項之一可能更適合您的實驗。

Kruskal-Wallis檢驗 3 個或更多組的中位數（而不是平均值）之間的差異。它僅作為“普通變異數分析”替代方案有用，沒有在重複量測中那樣匹配的主題。以下是解釋 Kruskal-Wallis測試結果的一些提示。

 Friedman檢驗正好相反，目的在替代匹配受試者的重複量測變異數分析。

變異數分析常見問題解答

1.ANOVA 中的簡單、主要和交互作用是什麼？

考慮包含要評估的兩種不同效果的雙因子 ANOVA 模型設置：

𝛼和𝛽因子是“主”效應，它們是給定因子的孤立效應。在一些教科書中，“主效應”與“簡單效應”互換使用。

交互項表示為“ 𝛼𝛽 ”，它允許一個因子的影響取決於另一個因子的水準。只有在您的研究中有重複時才能對其進行測試。否則，誤差項被假定為交互項。

2.什麼是多重比較？

當您對同一組數據進行多項統計檢驗時，更有可能發現並非真正差異的統計顯著差異。多重比較校正試圖控制這一點，並且通常控制所謂的族系誤差率。有許多多重比較測試方法，根據您的特定實驗設計和研究問題，它們都有優點和缺點。

3.“因子”一詞在單因子與雙因子變異數分析中是什麼意思？

在整體統計中，很難跟踪因子、組和尾部。對於未經訓練的人來說，“雙因子變異數分析”可能代表著這些事情中的任何一個。

考慮 ANOVA 的最佳方法是根據實驗中的因子或變數。假設您的分析中有一個因子（也許是“處理”）。您可能會看到它被寫成單因子變異數分析。即使該因子有幾個不同的處理組，也只有一個因子，這就是名稱的驅動力。

此外，“方式”與 t 檢驗之類的“尾巴”完全無關。 ANOVA 依賴於 F 檢驗，它只能檢驗相等與不相等，因為它們依賴於平方項。所以 ANOVA 沒有“一尾或二尾”的問題。

4.ANOVA 和 t 檢驗有什麼區別？

ANOVA 是 t 檢驗的擴展。如果您只有兩組平均值進行比較，請使用 t 檢驗。更多需要變異數分析。

5.變異數分析和卡方有什麼區別？

卡方設計用於列聯表或組內項目的計數（例如，動物的類型）。目標是查看特定樣本中的計數是否與您隨機期望的計數相匹配。

ANOVA 將受試者分組進行評估，但存在一些感興趣的數字反應變數（例如，葡萄糖水準）。

6.ANOVA 能否同時評估對多個反應變數的影響？

多個反應變數使事情比多個因子複雜得多。 ANOVA顯然可以處理多個因子，但它不是為一次跟踪多個反應而設計的。

從技術上講，有一種為此設計的擴展方法，稱為多變數（或多）變異數分析，或更常見的寫為 MANOVA。事情很快變得複雜，通常需要高級訓練。

7.除了通常的分類因子外，ANOVA 還能評估數字因子嗎？

聽起來您正在尋找 ANCOVA（協變異數分析）。您可以將連續（數字）因子視為分類因子，在這種情況下，您可以使用 ANOVA，但這是一個常見的混淆點。

8.ANOVA的定義是什麼？

ANOVA 代表變異數分析，顧名思義，它是一種統計技術，用於分析實驗因子如何影響實驗反應變數的變異數。

9. 什麼是ANOVA中的集區劃分(blocking)？

當您認為某個因子會嚴重影響結果時，阻止是一種非常強大且有用的實驗設計策略，因此您希望在實驗中對其進行控制。阻塞會影響如何在實驗中完成隨機化。通常集區劃分變數是對控制很重要但本質上不感興趣的討厭變數。

一個簡單的例子是評估一種藥物的檢定力並按受試者年齡進行阻斷的實驗。要進行分組，您必須首先收集研究中所有參與者的年齡，將他們適當地分組（例如，10-30、30-50 等），然後隨機分配相同數量的處理組每個組內的科目。

圍繞集區劃分有一個完整的研究區。一些示例包括具有多個區組變數、並非所有處理都出現在所有區組中的不完全區組設計，以及每個區組和處理組合中出現相同（或不等）重複數的平衡（或不平衡）區組設計。

10. 什麼是統計中的變異數分析？

對於單因子 ANOVA 檢驗，總體 ANOVA 無效假設是所有處理的平均反應相等。 ANOVA的 p 值來自 F 檢驗。