Marius Marusteri    , Vladimir Bacarea 

https://www.biochemia-medica.com/en/journal/20/1/10.11613/BM.2010.004

Abstract

對於生物統計學領域的初學者而言，選擇正確的統計測試方法有時可能是一項非常艱鉅的任務。

本文將提供有關選擇測試逐次分析過程，該過程用於比較兩個或更多組的統計差異。例如，我們將需要知道我們擁有的數據的類型（標稱，有序，間隔/比例），數據的組織方式，必須處理的樣本/組的數量，以及成對或是不成對。此外，我們必須問自己，這些數據是否來自非高斯母群或是高斯分佈數據。一個關鍵問題是，如果滿足適當的條件，應該使用單尾測試還是兩尾測試，後者通常是最有效的選擇。

  此文以Q / A（問題/答案）的方式提出了適當的方法，以向使用者提供完成此任務所必需而且更容易理解的基本概念。一些必要的基本概念是：統計推斷，統計假設檢定，應用統計檢定所需的步驟，參數與非參數檢定，單尾對比雙尾檢定等。

在本文的最後部分，將提出一種測試選擇演算法，該演算法基於一個適當的統計決策樹，用於一個，兩個或多個組的統計比較，以證明基本概念的實際應用。

一些有爭議的概念將在以後的其他文章中進行討論，例如異常值及其在統計分析中的影響，遺失數據的影響等。

引言

為了選擇正確的統計檢定，在分析實驗數據時，我們必須至少具有：

對一些基本的統計術語和概念有具體的理解。有一些與我們在研究/實驗過程中收集到的數據有關的方面的一些知識（例如，我們擁有什麼類型的數據-標稱，有序，間隔或比例，如何組織數據，有多少研究組（通常是實驗組和對照組） 。是成對的或不成對的組，並且是從常態分佈/高斯母群中提取的樣本）； 對我們的統計分析目標有很好的了解；為了避免某些錯誤，我們必須以結構良好的決策樹/演算法方式解析整個統計協議。

以下問題和答案將逐步介紹實現此目標所需的術語和概念。

問題1：需要哪些基本術語和概念？

答案1：推論是從前提中得出邏輯結果結論的行為或過程。

統計推斷或統計歸納包括使用統計和（隨機）抽樣來進行有關統計母群某些未知方面的推斷[1,2]。

它應與敘述性統計數據[3]加以區別開來，後者用於以定量術語描述數據的主要特徵（例如，對數據使用集中趨勢指標-例如平均值，中位數，眾數或分散指標-樣本方差，標準偏差等）。因此，敘述性統計的目的是定量地總結一個數據集，與推論/歸納統計相反，後者被用於支持有關認為該數據代表的母群的陳述。

通過使用推論統計，我們嘗試從從中抽取的隨機樣本推斷母群，或更普遍地說，從有限時間內觀察到的行為推斷隨機過程，如下所示圖（圖1）。 

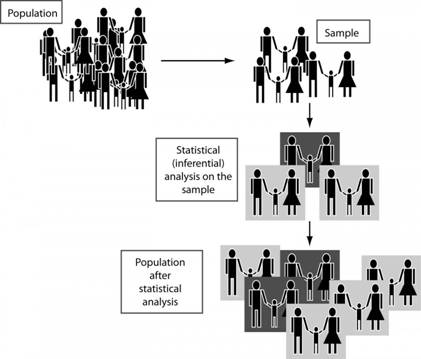
圖1.對樣本進行統計分析以推斷母群

統計推斷可能包括[3，4]：

點估計，包括使用樣本數據計算單個值（也稱為統計量），該值將用作未知（固定或隨機）母群參數（例如，相對風險RR = 3.72）。

2.區間估計是使用樣本數據來計算未知母群參數的可能（或可能）值的區間，  與點估計相反，點估計是單個數字（例如，RR的信賴區間95％CI為1.57-   7.92）。

我們必須了解，有時可以同時使用點估計和區間估計，以便通過從母群中提取的樣本來推斷母群的參數。

如果我們將“真實值”定義為使用完善的量測工具而不會犯任何類型錯誤的實際母群值，則我們將不得不接受，我們可能永遠不知道母群參數的真實值[4]。但是，使用這兩個估計量的組合，我們可以獲得一定的信賴度，即使我們的結果（點估計）不一定與真實值相同，真實值也可能在該區間內，如圖所示。下圖（2）。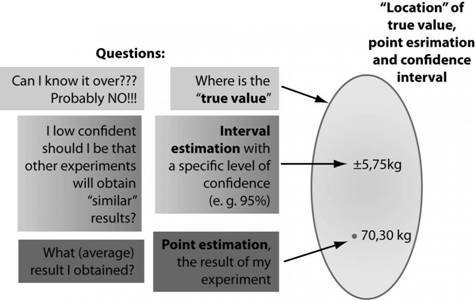  

圖2.真值，點估計和信賴區間的概念

3.Prediction/forecast- Forecast是未知情況下的估計過程。Prediction是一種聲明或主張，即特定  事件將在未來比forecast中更確定地發生，因此Prediction是一個相似但更籠統的術語。風險和不確定性對於forecast和Prediction至關重要。

4.統計假設檢定-最後但並非最不重要，進行統計推斷的最常見方法可能是使用統計假設檢定。這是一種使用實驗數據做出統計決策的方法，而這些決策幾乎總是使用所謂的“虛無假設”檢定來做出的。

虛無假設（H0）正式描述了一組數據某些方面的統計行為，並且除非數據的實際行為與該假設相矛盾，否則該描述將被視為有效。

因此，將原假設與另一個假設（所謂的“對立假設”, H1）進行對比。統計檢定實際上僅檢定原假設。虛無假設檢定採用以下形式：對於差異檢定，“各組之間沒有差異”。對於相關檢定，其為“沒有關聯”。人們永遠無法“證明”另一種假設。一個人只能拒絕原假設（在這種情況下，我們接受對立假設），或者接受原假設。

重要的是要了解，當前實際中使用的大多數統計協議都包含一個或多個涉及統計假設的檢定。

問題2：為什麼我們需要統計推斷及其主要指數-統計假設檢定？

答案2：簡而言之，因為我們需要以科學的方式證明，例如，在涉及兩個樣本的實驗中測得的參數平均值之間觀察到的差異，“具有統計學意義”[4]。

“統計上的顯著差異”僅表示有統計證據表明存在差異。這並不代表著就發現的效用而言，差異必然很大，重要或顯著。它僅表示樣本統計數據是母群參數的良好估計值的可量測概率。

為了更好地理解這一概念，我們舉個例子。我們採集了兩個人類受試者的樣品。一個接受治療和改良飲食的測試樣品，以及接受安慰劑和常規飲食的對照樣品。對於兩個樣品，記錄其體溫和體重。實驗結果列於表1。

如果我們根據“代數推理”來查看結果，我們可能會說，這些樣品的重量平均值之間的差異大於體溫平均值之間的差異。但是，當我們使用適當的統計檢定進行平均值之間的比較時（在這種情況下，適當的檢定是“未配對數據的t檢定”），結果將令人驚訝。統計學上唯一的顯著差異是體溫的平均值之間。與我們的常識和經驗所得出的結論恰恰相反。

顯然，我們需要進行統計（顯著性）檢定，以便得出某些東西已經或沒有達到“統計意義”的結論。統計或科學決策都不能可靠地基於“人眼”或觀察者“先前的經歷”的判斷。

必須注意的是，即使有統計學意義，研究人員也不能100％確定觀察到的差異。為了處理這種情況下的“不確定性”水準，引入了兩個（互補的）推論統計的關鍵概念：信賴水準（C）（例如信賴區間）和顯著性水準（α-alpha）[5]。

 簡單來說，顯著性水準（α或alpha）可以定義為在無效假設，實際上是真實的情況下，做出決定以拒絕無效假設的可能性（一種稱為I型錯誤或“偽陽性確定”的決定）。流行的顯著性水準為5％，1％和0.1％，根據經驗，對應的“信賴水準”為95％，99％和99.9％。

 表1.實驗結果

為了更好地理解這兩個術語，讓我們舉一個一般的例子。如果參數的點估計為P，且信賴水準為C，則信賴區間[x，y]，則在[x，y]區間之外的任何值都將與顯著性水準α= 1-C時的P顯著不同。用來生成信賴區間的相同分佈假設。

也就是說，如果在第二個參數的估計中，我們觀察到小於x或大於y的值，我們將拒絕原假設。在這種情況下，原假設為：“此參數的真實值等於P”，顯著性水準為α。相反，如果第二個參數的估計值位於[x，y]區間內，我們將無法拒絕該參數等於P的原假設。

問題3：應用統計檢定需要哪些步驟？

答案三：

1.有關要檢定的虛無假設和對立假設的陳述。

2.選擇顯著性水準（由希臘符號α表示。流行的顯著性水準為5％，1％和0.1％，對應於α的值0.05、0.01和0.001）。

3.根據正確的測試數學公式，計算相關測試的統計數據（S）。

4.將測試的統計數據（S）與相關的臨界值（CV）（從標準案例的表格中獲得）進行比較。在這裡我們可以得到所謂的“ P值”。

5.決定是“拒絕”原假設，或是贊成對立假設。如果S> CV，則決策規則將拒絕原假設（H0），反之亦然。實際上，如果P≤α，我們將拒絕原假設。否則，我們將接受[4]。

如果使用現代統計軟體，則第3步和第4步是由電腦透明完成的，因此我們可以直接獲取“ P值”，而不必查閱大型統計表。大多數統計方法提供測試統計的計算結果。

最後，當我們對實驗數據進行統計顯著性檢定時，我們獲得了一個所謂的“ P值”，它表示當虛無假設成立時觀察到我們的結果為極端甚至更極端的可能性[6] 。

如果返回表1所示的示例，則P值將回答該問題[7]。如果從中提取這兩個樣本的母群確實具有相同的平均值，那麼當樣本數量如此大時，在實驗中觀察到樣本平均值之間存在如此大差異（或更大）的可能性是多少？

因此，如果P值為0.04，則代表著有4％的機會觀察到與當兩個母群平均值實際上相同時，觀察到的差異有一樣大的差異（虛無假設為真）。因此，很容易得出這樣的結論：我們觀察到的差異有96％的機會反映了母群之間的真實差異，而差異是由機會造成的概率為4％。這是一個錯誤的結論。我們可以說的是，在96％的實驗中，來自相同母群的隨機抽樣所導致的差異小於我們觀察到的差異（即保留了原假設），並且大約等於或大於我們在4％的觀察中得出的差異實驗。

選擇正確的統計檢定。開始統計分析之前，我們需要了解什麼？

問題4：我們可以在實驗期間獲得哪些類型的數據

答案4：從實驗中收集的基本數據可以是定量（數值）數據或定性（分類）數據，它們都具有某些子類型[4]。

定量（數值）數據可以是：

1.離散（不連續）數字數據，如果可能的數值只有有限數目，或者數字行中每兩個可能的值之間有空格（例如，來自過時的基於汞的溫度計的記錄）。

2.連續數據，由其餘的數字數據組成，不能將其視為離散的。這是一種數據類型，通常與使用最新科學儀器進行的某種高級量測相關。

更重要的是，可以間隔或比例級別量測數據。出於統計分析的目的，兩個量測級別之間的差異並不重要。

1.間隔數據-間隔數據沒有絕對的零，因此說一個水準代表該水準平除以2的兩倍是沒有道理的。例如，儘管以攝氏度為單位量測的溫度在度數之間具有相等的間隔，但它沒有絕對零值。攝氏溫度標度的零表示水的凝固點，而不是溫度的總和。說攝氏10度的溫度是攝氏5度的兩倍是沒有道理的。

2.比例數據-比例數據的絕對值為零。例如，量測長度時，零表示沒有長度，而10米長則是5米的兩倍。

間隔和比例數據均可用於參數測試。

定性（分類）數據可以是：

1.二進制（邏輯）數據-分類數據的基本類型（例如，正/負；當前/不存在等）。

2.標稱數據-在更複雜的分類數據上，第一（也是最弱）數據稱為標稱數據。標  稱級別數據由僅按名稱區分的值組成。此數據沒有標準的排序方案（例如羅馬尼亞人，匈牙利人，克羅地亞人等）。

序數（排名）數據-分類數據的第二級稱為序數數據。序數數據與標稱數據相似，因為按名稱區分數據，但與標稱級別數據不同，因為存在排序方案（例如，小型，中型和高級）。

問題5：在開始統計分析之前，如何組織這些數據類型？

答案5：原始數據是指未經處理或任何其他操作（原始數據）在源上收集的數據（原始數據）[4]。

因此，原始數據是在科學研究期間收集的，需要將其轉換為某種格式，以允許在變量之間進行解釋和分析。

通常，使用數據庫管理系統（Microsoft Access，Oracle，MySQL甚至專用的電子病歷系統）或電子表格軟體（例如Microsoft Excel或OpenOffice Calc）收集來自實驗的數據。在這兩種情況下，為了準備進行統計分析，必須將研究數據導出到允許使用該數據的方法。必須使用具有適當數量的行和列的表以表格形式（類似於電子表格）來組織它們，這是大多數統計軟體所使用的格式。

如果必須處理數字數據，則可以兩種方式組織這些數據，具體取決於我們將使用的統計軟體的要求：

1.索引數據–當我們至少有兩列時：一列將包含實驗期間記錄的數字，另一列將包含“分組變量”。這樣，僅使用表的兩列，我們就可以記錄大量樣本的數據。這種方法用在眾所周知的功能強大的統計軟體中，例如SPSS（由SPSS Inc.，現在是IBM的子公司開發），甚至在免費軟體中，如Epiinfo（由疾病控制中心開發，http：//www.cdc .gov / epiinfo / downloads.htm）或OpenStat（由Bill Miller開發，http：//statpages.org/miller/openstat/）。

2.原始數據–當針對我們可能擁有的每個樣本使用特定列（行）來組織數據時。即使從初學者的角度來看，這種方法可能更直觀，但它仍然被相對少量的統計軟體（例如，由Graphpad Software Inc.開發的MS Excel Statistics加載項，OpenOffice Statistics或非常直觀的Graphpad Instat and Prism使用） ）。

  如果我們記錄的數據是定性（分類）數據，則應將主數據表匯總到列聯表中。列聯表本質上是一種顯示格式，用於分析和記錄兩個或多個分類變量之間的關係。基本上，列聯表有兩種類型：“ 2 x 2”（具有2行2列的表）和“ N x N”（其中N> 2）。

問題6：我們可以有多少個樣本？

答案6：根據研究/研究設計，我們可能會遇到三種情況[4,7]：一個樣品，兩個樣本；三個或更多樣本。

如果我們只有一個樣本，我們可能會問一個相關的問題：由於似乎沒有明顯的比較用語，可以做出什麼統計推斷？

即使看起來像是一個難題，仍然可以進行一些統計分析。例如，如果我們對   一隻實驗動物樣本使用熱解藥，我們仍然可以在實驗過程中記錄的平均體溫與該種動物的已知“正常”值之間進行一些比較，為了證明這些值之間的差異是否具有“統計學意義”，並得出該藥物是否具有某些熱原作用的結論。

如果研究涉及兩個樣本（這是最常見的情況之一），我們要做的就是遵循推論統計的正確協議，以便在樣本之間進行方便的比較。

當涉及兩個以上的樣本時，分析似乎要複雜一些，但是有可用的統計檢定，比處理此類數據的能力還強。例如，我們可以使用變方分析（ANOVA檢定）來比較一個實例中所有樣本的平均值。

同樣，我們必須知道，如果在變方分析的第二階段拒絕了虛無假設，則可以使用某些事後檢定，並且能夠對實驗中的每對樣本進行比較。

問題7：我們是否有依賴或獨立的樣本/成對或不成對的組？

答案7：總的來說，每當一個組（樣本）中的對象與另一組（樣本）中的對象相關時，這些樣本就被定義為“成對”。

例如，在一項關於母女的研究中，將樣本與母親和女兒配對。兩個樣本中的主題並非彼此獨立。對於獨立樣本，被選擇的母群成員的概率完全獨立於被選者自己的組或研究中其他任何組的被選對象[7]。

配對數據可以定義為通常落入成對的值，因此可以預期成對的數據比成對的數據變化更大。如果不滿足這些條件，我們將不得不處理未配對或獨立的樣本。

為什麼這個這麼重要？因為有許多統計測試對配對/未配對的樣本具有不同的版本，所以使用不同的數學方法可能會導致不同的結果。例如，眾所周知的統計檢定（用於比較兩個樣本的平均值的t檢定）對成對/不成對的樣本具有不同的版本：成對（相關）的樣本t檢定和不成對（獨立）的樣本t檢定。

因此，選擇配對測試（針對相關樣本的測試）而不是未配對測試（針對獨立樣本的測試）是錯誤的，並且可能導致統計推斷過程中的錯誤結果/結論。

當實驗遵循以下設計之一時，我們必須選擇配對測試[7]：

  1.當我們在對每個主題進行干預之前和之後量測變量時；

  2.當我們成對地招募受試者時，要匹配年齡，種族或疾病嚴重程度等變量， 這對中的一個會接受一種治療；另一個得到替代治療；

  3.當我們進行幾次實驗室實驗時，每次都與對照和處理過的製劑並行處理；

  4.當我們在子/父母對（或任何其他類型的相關對）中量測結果變量時。

廣義上講，每當我們期望一個樣本中的一個值比另一個樣本中的一個隨機選擇的值更接近另一個樣本中的特定值時，我們就必須選擇一個配對測試，否則我們選擇一個獨立的樣本測試。

問題8：是否從常態/高斯分佈中採樣數據？

答案8：基於分佈的常態性，我們選擇了參數檢定或非參數檢定。

我們應該知道，許多統計檢定（例如t檢定，變方分析（ANOVA）及其變數）都先驗地假設我們從遵循高斯（常態/鐘形）分佈的母群中採樣數據。遵循此假設的測試稱為參數測試，而使用此類測試的統計科學分支稱為參數統計[4]。

參數統計假設數據來自某種概率分佈（例如常態分佈），並推斷分佈的參數。但是，從中量測數據的許多母群（生物學數據通常都在這一類別中）永遠不會精確地遵循高斯分佈。高斯分佈在兩個方向上都無限延伸，因此既包括無限低的負數又包括無限高的正數，並且生物學數據通常在範圍上自然受到限制。儘管如此，許多生物數據的確呈近似高斯的鐘形。

因此，即使分佈僅近似於高斯分佈（特別是對於大樣本，例如> 100個主題），ANOVA檢定，t檢定和其他統計檢定也能很好地發揮作用，並且這些檢定在許多科學領域中都是常態使用的。

但是在某些情況下，例如，當我們不得不處理少量樣本（例如<10）或將醫療評分（例如Apgar評分）作為結果變量時，應用這樣的檢定假設母群遵循常態分佈，而沒有對現象的正確了解，可能會導致產生誤導的P值。

因此，統計的另一個分支稱為非參數統計，提出了無分佈的方法和檢定，這些方法和檢定不依賴於假設數據是從給定的概率分佈（在本例中為常態分佈）中得出的。這種檢定稱為非參數統計檢定[4]。我們應該知道，幾乎每個參數統計檢定都有對應的非參數檢定。

當我們通過統計協議時，最困難的決定之一可能是在參數測試還是非參數測試之間進行選擇。我們可能要提出的一個相關問題是：非參數檢定是否不依賴於假設數據是從常態分佈中得出的假設，為什麼不僅使用此類檢定以避免錯誤？

要了解這兩種測試之間的區別，我們必須了解統計中的兩個更多基本概念：統計測試的強韌性和檢定力。

可靠的統計測試即使在某種程度上違反了其假設，也可以表現良好。在這方面，非參數測試往往比其參數等效更強韌，例如通過能夠處理非常小的樣本（數據遠非常態分佈），可以使非參數測試更加強韌。

統計檢定的檢定力是當對立假設為真時，檢定將拒絕原假設的概率（例如，不會產生II型錯誤）。正如Ilakovac[6]先前已廣泛審查的那樣，II型錯誤也稱為“第二類錯誤”，β錯誤或“假陰性”，並且被定義為未能拒絕虛無值的錯誤。假說實際上是不正確的。隨著檢定力的增加，II型錯誤的可能性降低。非參數測試往往更健壯，但通常檢定力較低。換句話說，可能需要更大的樣本量才能以相同的信賴水準得出結論[7]。

問題9：何時可以選擇適當的非參數檢定？

答案9：在以下情況下，我們絕對應該選擇非參數檢定[7]：

結果變量是少於十二個類別的等級或分數（例如Apgar分數）。顯然，在這些情況下，母群不能為高斯分配。

當樣本大小太小（<10左右）時，可能會出現相同的問題。

當一些值超出範圍時，太高或太低而無法使用特定的量測技術進行量測。即使母群呈常態分佈，也無法通過參數檢定（例如t檢定或ANOVA）分析樣本數據。對此類數據使用非參數檢定很容易，因為它不會依賴於數據是從常態分佈中得出的假設。非參數測試通過將原始數據重新編碼為等級來工作。極低值和極高值被分配一個等級值，因此不會像使用包含極值的原始數據那樣使分析失真。沒幾個值不能精確量測也沒關係。

當我們有足夠的“統計信心”時，母群遠非常態分佈。可以使用多種“常態性檢定”來檢定樣本數據的常態分佈。

常態性檢定用於確定數據集是否通過常態分佈很好地建模。換句話說，在統計假設檢定中，他們將根據常態分佈的原假設對數據進行檢定。

此類測試的最常見示例是：

1. D’Agostino-Pearson常態性檢定–計算偏度和峰度，以量化不對稱和形狀分佈與常態之間的距離。然後，它計算這些值中的每一個與常態分佈所期望的值相差多少，並根據這些差異的總和來計算單個P值。它是一種功能強大且功能強大（相對於其他標準）的常態性測試，並且在一些現代統計書籍中得到推薦。

2.過去經常使用的Kolmogorov-Smirnov檢定將數據的累積分佈與預期的累積常態分佈進行比較，並將其p值僅基於最大差異，這不是評估常態性的非常敏感的方法，因此變得過時了。

3.除了這兩個以外，還有相對大量的其他常態性檢定，例如：Jarque-Bera檢定，Anderson-Darling檢定，Cramér-von-Mises準則，Lilliefors檢定常態性（本身是Kolmogorov- Smirnov檢定），Shapiro-Wilk檢定，Shapiro-Francia檢定常態性等。

使用常態性檢定似乎是決定我們是否必須使用參數或非參數統計檢定的簡便方法。但事實並非如此，因為在使用此類測試之前，我們應注意樣本的大小。對於小樣本（例如<15），常態性測試不是很有用。他們幾乎沒有能力區分高斯母群和非高斯母群。小樣本根本沒有包含足夠的資訊，無法讓我們推斷整個母群分佈的形狀。下表將以簡單的方式總結以上討論（表2）。

表2.參數測試與非參數測試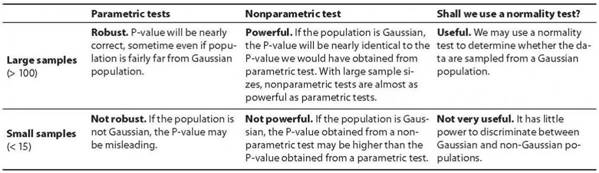

如果數據不遵循高斯（常態）分佈，則我們可以對這些值進行轉換以建立高斯分佈[4]。如何做到這一點不是本文的主題，但是作為一個很好的例子，對於量測值（數值數據），一種簡單的方法是使用對數轉換：新值= log（舊值）。

在某些情況下，這種簡單的方法可能允許我們使用參數統計檢定而不是非參數檢定。

問題10：我們應該選擇單尾還是雙尾測試？

答案10：假設我們設計了一些研究/實驗來比較世界上各個國家（例如瑞典和韓國之間以及羅馬尼亞和保加利亞之間的年輕人）（18-35歲）的身高。因此，在進行統計分析時，已制定了無效假設H0（例如，這兩個獨立樣本的平均高度之間沒有差異），並且已制定了針對特定統計檢定的對立假設H1。讓我們認為分佈是高斯分佈，目標是執行特定檢定以確定是否應拒絕原假設，而採用對立假設（在這種情況下，針對未配對/獨立樣本的t檢定將是相關）。

但是，可以執行兩種不同類型的測試[4,7]。

單尾測試僅尋找參數的增加或減少（單向變化），而雙尾測試則尋找參數的任何變化（可以是任何變化-增加或減少）。

為了理解這個概念，我們必須定義假設檢定的關鍵區域：所有結果的集合，如果這些結果出現，將導致我們決定拒絕虛無假設，而支持對立假設。

在單尾測試中，關鍵區域將只有一部分（下圖中的灰色區域）。如果我們的樣本值位於該區域，則我們拒絕虛無假設，而選擇另一假設。在兩尾測試中，我們正在尋找增加還是減少。因此，在這種情況下，關鍵區域包括兩個部分，如圖3所示。 

圖3.單尾和雙尾測試中的關鍵區域

比較兩組時，我們必須區分單尾和雙尾P值。兩尾P值回答了這個問題：假設虛無假設是正確的，那麼隨機抽樣的樣本與我們在本實驗中觀察到的平均值更大（或更大）的平均值相比有什麼機會呢？

要解釋一個單尾P值，我們必須在收集任何數據之前預測哪個組的平均值會更大。單尾P值回答了這個問題：假設原假設為真，那麼隨機抽樣的樣本與本次實驗所觀察到的平均值較大的指定組相比，平均值有多少距離（或更大）？

僅當先前的數據，物理限制或常識告訴我們，差異（如果有）只能沿一個方向傳播時，單尾P值才合適。或者，我們可能只對一個方向的結果感興趣。例如，如果已經開發出一種新藥來治療存在較舊藥物的疾病。顯然，如果新藥的性能優於舊藥，研究人員只對繼續研究感興趣。如果新藥的性能與舊藥相同或更差，則將接受虛無假設。

因此，這裡的真正問題是我們是否對實驗情況有足夠的了解，以知道差異只能在一個方向上發生，還是我們只對兩個方向上的組差異感興趣。

鑑於上述情況，考慮到上述研究，我們只有在比較瑞典和韓國之間成年男性的身高平均值時才可以選擇單尾檢定，因為我們的常識和經驗告訴我們，如果任何人，都只能朝一個方向前進（成年男性瑞典公民應比韓國公民高）。

當我們對羅馬尼亞和保加利亞公民進行相同的分析時，此假設可能不準確，因此我們將不得不選擇雙尾檢定。

僅當滿足以下兩個條件時，才應選擇一個單尾P值：

首先，在收集任何數據之前，我們必須先預測哪個組的平均值會更大；

如果另一組的平均值較大（即使該平均值較大），則我們必須將該差異歸因於機會。

由於所有這些原因，特別是對於初學者，除非我們有充分的理由選擇單尾P值，否則建議選擇正確的兩尾測試而不是單尾測試。

問題11：我們的統計分析的目標是什麼？

答案11：使用基本統計分析時，我們最多可以有三個主要目標[4,7]：

比較一個，兩個或多個組/樣本的平均值（或中位數）（例如，對照組中的血壓是否高於治療組的血壓？）。

進行某種關聯，以查看一個或多個自變量與一個因變量之間的關係（例如，

體重和/或年齡如何影響血壓）。

量測一個或多個自變量（例如流行病學危險因素）與一個或多個因變量（例

如疾病）之間的關聯。這就是所謂的列聯表分析，在這裡我們可以研究自變量（例如吸煙或大量吸煙）如何與一個或多個因變量（例如肺癌及其各種形式）相關聯。

即使有三個目標，我們在這裡僅討論第一個目標：一個，兩個或多個組/樣本之間的平均值比較。根據我們擁有的樣本數量，我們的目標是對以下問題提供科學的答案：

對於一組/樣本：我們已經在該樣本中量測了一個變量，其平均值與假設（“正常”）值不同。這是偶然的緣故嗎？還是它告訴我們觀察到的差異是顯著的差異？

對於兩組/樣本：我們在兩組中量測了一個變量，平均值（和/或中位數）似乎不同。那是偶然的緣故嗎？還是說這兩組人真的不同？

對於三個或更多組/樣本：我們已經對三個或更多組中的變量進行了量測，平均值（和/或中位數）不同。那是偶然的緣故嗎？還是說這兩個團體真的不同？哪些群體與其他群體不同？

為了對此類問題提供科學的答案，我們必須使用以下統計檢定之一比較這些組/樣本的平均值（中位數）（建議使用雙尾檢定，除非我們有充分的理由選擇單尾測試）（表3）。

現在，了解基本術語和概念，從上表中給出的測試中選擇測試的過程，如果我們將以一種演算法的方式進行思考，解析適當的決策樹（例如，圖3中給出的決策樹），則將非常容易理解。如圖4所示，以避免在過程中出現任何錯誤。

圖4.正確的統計檢定的選擇過程

表3.統計測試，用於比較一個，兩個，三個或更多組/樣本的平均值（中位數）

結論

正確的統計測試的選擇過程可能是一個艱鉅的任務，但是對適當的統計術語和概念的充分了解和理解，可以會導致我們做出正確的決定。

特別是，我們需要了解我們可能擁有的數據類型，這些數據是如何組織的，我們必須處理的樣本/組的數量以及它們是成對的還是不成對的；我們必須問問自己，是否為非高斯母群繪製了高斯數據，並且如果滿足適當條件，則選擇單尾檢定（相對於兩尾檢定，通常是推薦選擇）。

基於此類資訊，我們可以遵循適當的統計決策樹，使用能夠將我們引導至正確測試的演算法方式，在測試選擇過程中不會出現任何錯誤。

即使我們在這裡沒有討論涉及兩個或多個因素（例如雙因素變方分析）或統計推斷的其他兩個主要目標（列聯表分析和相關/回歸分析）的平均值比較，該演算法也將很有用同樣在這種情況下，使用相同的方法選擇正確的統計檢定。

儘管如此，一些有爭議的概念仍將在以後的其他文章中進行討論，例如離群值及其在統計分析中的影響，缺失數據的影響等。

References

 1. Cox DR. Principles of statistical inference. Cambridge University Press, 2006.

 2. McHugh ML. Standard error: meaning and interpretation. Biochem Med

   2008;18:7-13.

 3. Slavkovic A. Analysis of Discrete Data. Available  at:http://www.stat.psu.edu/online/courses/stat504/01_overview/index.html. Accessed:  October 24, 2009.

 4. Marusteri M. [Notiuni fundamentale de biostatistica:note de curs]/Fundamentals  

   in biostatistics:lecture notes. University Press Targu Mures, 2006. (in Romanian)

 5. Simundic AM. Confidence interval. Biochem Med 2008;18:154-61.

 6. Ilakovac V. Statistical hypothesis testing and some pitfalls. Biochem Med

   2009;19:10-6.