|
https://www.biochemia-medica.com/assets/images/upload/xml_tif/McHugh_ML_-Multiple_comparison_analysis_testing_in_ANOVA.pdf
摘要
長期以來,變方分析(ANOVA)測試一直是研究人員對多個實驗組和一個或多個對照組進行研究的重要工具。但是,ANOVA無法提供有關各個研究組之間差異或研究組複雜組合的詳細資訊。為了完全了解變方分析中的組間差異,研究人員必須對特定的實驗組和對照組之間的差異進行測試。對先前在另一分析中測試過的數據子集進行的測試稱為事後測試。此類事後測試為ANOVA結果提供了此類詳細資訊,稱為 “多重比較分析”測試。最常用的多重比較分析統計資訊包括以下測試:Tukey,,Newman-Keuls,Scheffee ,Bonferroni
and Dunnett.。這些統計工具各有特定的用途,優點和缺點。有些最適合用來檢驗理論,而另一些則可以用來產生新理論。選擇適當的事後測試將為研究人員提供最詳細的資訊,同時可以限制因α膨脹而導致的Type 1錯誤。
使用多重比較分析測試
一旦變方分析(ANOVA)測試完成,研究人員可能仍需要了解不同實驗組和對照組之間的子組差異。子組差異稱為“成對”差異。變方分析不能提供成對差異的檢驗。當研究人員需要測試成對差異時,需要進行稱為事後測試的後續測試。
變方分析的輸出不提供成對差異的任何分析,那麼研究人員應如何調查經變方分析測試後的各個子組之間的差異?想到的第一種方法是在每個感興趣的成對之組間執行許多t檢驗。這不是一個好方法有兩個原因:首先,對同一數據進行重複的統計檢驗,這是對每對興趣進行t檢驗的結果,將導致alpha膨脹[1]。其次,結果仍然無法解釋,因為單個t檢驗一次只能檢查兩組。而變方分析中的每個子組都有自己的平均值。當使用重複的t檢驗來檢驗ANOVA的成對差異時,平均值總數(即平均值計數,每個實驗組和對照組均不包括在內)從分析中排除。忽略ANOVA中存在更多子組平均值的事實,將人為的增加顯著的成對差異的數量。更糟糕的是,如果將某些子組排除在事後檢驗中,則各個成對t統計量將更大。因此,使用t檢驗檢查成對差異可能會高估單個t檢驗的大小。這代表著來自所有成對t檢驗的t值之和,通常會超過由多個比較分析統計數據[2]之一產生的t統計量的值。結果執行多個t檢驗將使研究人員出現I型錯誤的可能性更高。也就是說,研究人員更有可能報告一些沒有實際差異的配對之間的顯著差異[1]。
執行多個成對的t檢驗會導致另一個問題。研究人員可能希望測試一個或多個研究組與一組特定組合研究組之間的差異。成對t檢驗不能執行這種分析。但是,有一種多元統計數據可以克服成對t檢驗方法的所有局限性。此類統計資訊稱為多重比較分析。在完整的變方分析發現有重要差異之後,應使用多重比較分析統計數據之一來檢查成對和子組差異。成對差異的關鍵測試包括:Bonferroni,Sheffèe ,Tukey,Newman-Keuls和Dunnett。
多重比較分析(MCA)測試中的每一個方法都有其特定的優勢和局限性。有些會自動測試所有成對比較,而另一些則允許研究人員將測試限制為僅感興趣的配對或子組。每種方法都對alpha膨脹和研究人員可以從測試中得出的答案產生影響。因此,MCA統計數據的選擇,以及關於使用哪個統計數據的所有選擇[3],都應基於特定的研究問題。例如,研究人員可能有一個特別感興趣的實驗組,應與每個對照組分別進行比較。或者研究人員可能希望將一個實驗組與所有對照組的組合進行比較,或僅與某些對照組進行比較,甚至與一個或多個其他實驗組進行比較。
研究中出現了許多不同的情況,可能會影響多重比較測試的選擇[3]。例如組群的樣本大小可能不相等。因此專門開發了一項多重比較分析測試來處理數據不相等的群體。檢定力可能是一項研究中的問題,某些測試比其他測試具有更大的檢定力。在某些研究中,所有比較的測試都非常重要,而其他研究僅需要對實驗組或對照組的預定組合進行測試。當特殊情況影響所需的特定成對分析時,多重比較分析測試的選擇必須依據特定統計數據感興趣的解決問題,和要分析的數據類型的能力來控制。
對比類別
對比是對ANOVA中兩組平均值之間差異的檢驗。通過ANOVA進行測試的組之間有兩種對比,簡單對比和複雜對比。一個簡單的對比是測試任意兩對之間的差異,例如實驗組1和對照組2 。複雜的對比是對組組合之間差異的測試。複合的對比一個例子是通過結合產生的子組之間的差異的試驗,例如的試驗組1,和4相結合,並通過組合產生的子組控制組1和3。 ANOVA的目的是測試理論或產生理論,並且可以使用多重比較分析來支持其中一項目的。
成對比較對測試
Tukey法
Tukey的多重比較分析方法針對每個對照組測試每個實驗組。如果實驗組和對照組之間的組大小不相等,則首選Tukey方法。Tukey方法通過首先測試最大的成對差異來進行。Tukey使用“ q”統計量來確定組差異是否具有統計學意義。“ q ”統計量是通過從總平均值中減去最小平均值,然後將該乘積除以平均值的總體組標準誤差得出[4]。平均值的總體組標準誤差除以樣本大小稱為內均方差(MS w ),並且是幾乎所有統計分析程序中ANOVA輸出提供的輸出值[5]。該q的值可以比對統計表中的q值,以確定該q值與特定一對超過臨界q值,因此達到統計顯著性。如果q值達到或超過臨界值,即兩組的差異有統計學顯著。
注意:通常使用一尾測試,因為從ANOVA中已經知道了組平均值。
如果第一對的平均值差異顯著(如果總體ANOVA顯著,情況將如此),則測試第二對。繼續成對測試,直到獲得的q值不顯著為止。不需要測試其他任何東西,因為它們不會很重要。Tukey使用相當保守的alpha估計。它會像一個組群一樣測試所有對比,因此,發現配對之間差異的能力要弱一些。在這種情況下,組群指的是組群錯誤率[6]。該術語解決了發生I型錯誤並因此導致錯誤發現的可能性。組群測驗減少了對重要性作出虛假陳述的可能性[6],並且當虛假報告重大差異的後果大於沒有發現差異的後果時,應使用組群測驗。組群測試為結果提供了更多的信心,因為此類測試幾乎不會產生I型錯誤[5,7 ]。
利用Tukey統計數據很好的的一個例子是一項研究,其中四種不同的抗生素被用於治療Multiple-Drug
Resistant Staphyloccus Aureus(MRSA)感染。假設控制組處理為只使用Vancomycin所述標準的治療藥物。並且有三個新的抗生素構成三個實驗組。小組人數可能會有所不同,這就是使用Tukey的原因之一。但是使用Tukey的最重要原因是,與Type
II錯誤相比,犯I類錯誤會有要更大的麻煩。原因是發生I型錯誤代表著研究人員得出的結論是,一種或多種實驗藥物比Vancomycin更有效。如果事實是Vancomycin比實驗藥物具有同等或更有效的檢定力,那麼I型錯誤的後果要遠大於II型錯誤。在此示例中,I型錯誤將導致臨床醫生使用效果較差的實驗藥物,該藥物的花費也可能比Vancomycin高得多。結果將是更多的死亡和更高的治療費用。但是得出II型錯誤只會使治療方案保持不變。因此Tukey的保守alpha值可能會導致更多的Type
II錯誤,但它將有助於研究人員避免Type
I錯誤。
Tukey方法的優點是,它可以測試所有成對的差異,它易於計算,並減少了產生I型錯誤的可能性。對於不相等的組樣本大小,它也是可靠的。它的主要缺點是它不如其他一些測試強大,並且其設計目的不是測試複雜的比較。
Newman-Keuls方法
Newman- Keuls方法與Tukey測試非常相似,不同之處在於它分別考慮了每種可能的對比度的alpha。因此,這不是組群對比測試。最終這是一個比Tukey更強大的測試,因為它執行了更多的成對比較。因此更有可能發現一些差異具有統計意義。最初它執行與Tukey測試運行相同的成對比較。對於那些初次比較,它具有與Tukey相同的功能。然後針對總體平均值對每個組平均值進行測試。這種增加的檢定力的代價是發生I型錯誤的可能性更大。它應當注意的是,用於Newman-
Keuls與每個後續測試而使用Tukey於所有測試的相同的臨界值減小。這就是Tukey保留alpha的方式,而Newman- Keuls方法在發現更多具有統計學意義的α值更保守。
該統計應用於相對較小的成對差異很重要的研究中。這種研究的例子包括幾乎所有對非常新的和少為人知的現象的研究。例如當艾滋病流行時,沒有藥物可以治療感染,即使治療藥物之間的微弱差異也很重要。由於沒有治療感染的藥物,因此對延長壽命有效的藥物非常重要。憑藉更強大的功能,Newman- Keuls統計將比功能更弱的測試(例如Tukey)更適合使用。同樣在此例子中,當沒有替代治療方法時,I型錯誤的危害不如拒絕不可避免的致命疾病的有效藥物那麼有害。治療諸如癌症和艾滋病等致死性疾病的歷史表明,大多數人寧願冒險嘗試一種可能無濟於事或可能造成傷害的藥物,而不願無所作為。
總之,Newman- Keuls統計量適用於即使很小的差異也很重要,並且II型錯誤的後果比I型錯誤的後果更嚴重的研究。這使得它成為對未知現象知之甚少的新科學領域的有用工具。這就是經典理論發展的研究狀況。其他統計數據應用於更發達的研究領域,並且當差異必須相對較大時才能使新療法優於現有療法。Newman -Keuls應該用於產生相同群體規模的研究。
比較多個組的測試
Tukey和Newman-Keuls測試目的在於測試簡單比較。當實驗組和對照組的組合構成的研究者必須測試子組,其它統計其應該使用可以測試複雜的比較。此類別中最常用的統計是Scheffee ,Bonferroni和Dunnett統計。
Scheffee方法
Scheffee方法測試所有可能的對比,簡單又複雜。如果它被稱為提前,所有的對比將要測試的Scheffee方法比所有其他兩種方法稍微更強大。如果僅要測試選定的對比,則是另一種稱為Bonferroni多重分析測試是更好的方法。因此,Scheffee和Tukey檢驗一樣,是在預測差異較小且II型錯誤的後果超過I型錯誤的後果時更適合使用的測試。所述Scheffee測試假定在ANOVA相等大小的實驗組和對照組。
當預測研究人員期望找到的群體差異的理論,在沒有得到很好的發展或檢驗時,首選Scheffee方法,因為它可以檢驗所有可能的比較。在沒有足夠的先前研究來驗證解釋變方分析發現的理論的情況下,事後測試需要更多的探索性數據分析。該Scheffee是一個很好的探索統計方法,因為它測試所有可能的比較。結果,它使研究人員可以觀察到哪些組或組的組合產生了原始ANOVA測試中發現的顯著差異。這是一種探索性數據分析的方法,是一種發現研究組之間先前未知的差異,或發現是否可以支持基於非常有限的理論的假設的策略。
如果理論發展良好,Scheffee可能也是一個不錯的選擇。發達的理論應該預測所有群體和群體組合的差異。鑑於Scheffee檢驗了所有可能的差異,因此很好地檢驗了發達理論的多個命題。即使可以分析所有可能的比較,Scheffee還是所有多元分析都限制了alpha膨脹問題。將Scheffee用作理論檢驗統計量,當Scheffee發現該理論所預測的差異時,該理論便得到確認。當理論預測其他群體之間沒有差異時,Scheffee在理論沒有發現其他群體之間存在顯著差異時,就證實了該理論。該Scheffee測試是理想的非常發達測試,因為,以最小的α膨脹,它測試所有可能的配對差異,包括對組合理論。
當理論發展不足以可靠地預測哪些對和對的組合會顯著不同時,Scheffee檢驗也是一個很好的工具。即使分析中的兩個或多個組沒有顯著差異,整體變方分析也可以產生顯著的F檢驗。準確地找出哪些組差異產生了顯著的F檢驗通常很重要。在這種情況下,要發現變方分析中哪些組存在顯著差異,研究人員必須進行多次比較分析。例如,假設在壞死性筋膜炎患者中測試了四種不同的抗生素的死亡率。變方分析可以確定的是,各組的死亡率之間是否存在顯著差異。它無法確定哪種藥物的死亡率最低,或者兩種或三種藥物的等效性和一種無效。該Scheffee方法提供了有關每個藥物的詳細資訊。
通過Scheffee檢驗,研究人員可以通過測試所有可能的對比來發現有意義的對比,從而進行理論生成研究。這種研究有助於研究人員從現有數據中得出偶然發現。並且是探索性數據分析中發現科學的一部分。可以檢測到以前未知的差異,研究人員通過解釋觀察到的差異的方法來創建新的理論。這種方法產生的理論應在專為測試新理論而設計的後續研究中進行測試。這是非常很重要因為在探索性數據分析中發現虛假關係的可能性比理論測試過程中更高。在這種類型的研究中更容易出現1型錯誤,發現的差異應通過後續研究予以證實。
隨後測試通過Scheffee方法發現的特定子組對比的研究應使用Bonferroni方法,該方法更適合於理論測試研究。該Bonferroni方法是I型誤差比不敏感Scheffee方法。
Bonferroni (Dunn)方法
像Tukey方法一樣,多重比較的Bonferroni方法是一種組群對比比較方法,因此它不會像其他類型的多重比較分析(例如Newman- Keuls方法)那樣將alpha膨脹。此外,與Scheffee方法一樣,Bonferroni方法可以測試複雜的成對。但是Bonferroni統計資訊不是用於探索性數據分析的工具。它要求研究人員預先指定所有要測試的對比。研究人員必須對感興趣的現像有足夠的理論,以便知道要指出的對比。結果,與諸如Scheffee之類的探索性方法相比,這是一個更好的檢驗實驗組結果理論的方法。由於Bonferroni將測試次數限制為研究人員事先指定的測試次數,因此減少了alpha膨脹的問題。Bonferroni方法的最大優點是通過限制alpha膨脹,可以降低I型錯誤的可能性。但是它不能偶然發現因此,由於並非所有差異都經過測試,因此提供的組間差異資訊較少。
Dunnett方法
Dunnett檢驗方法是一種特別有用於測試對照組的設計。它是一個特別強大的統計數據,因此可以發現組之間或組組合之間的相對較小但明顯的差異。Dunnett檢驗當研究者希望測試兩個或更多個實驗組與針對單個控制組的方法是非常有用的。它測試每個實驗組的平均值與對照組的平平均值。其他方法將每個研究組與總組平均值(即總體平均值)進行比較。測試方法的這種差異使Dunnett方法更有可能發現顯著差異,因為大的平均值包括所有分組平均值,因此從數學上講,它不如單個分組平均值那麼極端。與將一組平均值與最大平均值進行比較的測試相比,更極端的組平均值會產生更大的平均值差。所述Bonferroni方法可以被指定到測試僅針對單個對照組實驗組,但考慮到其研究組裝置比較針對總平均值,比Dunnett檢驗方法有更少的檢定力。
有各種各樣的事後檢定可進一步表明的組間差異,在ANOVA檢驗有助於顯著性檢驗。每個測試都有特定的應用程序,優點和缺點。因此,選擇與數據最匹配的測試,有關組間比較的資訊種類以及必要的分析能力非常重要。從理論生成與理論測試的角度選擇適合研究情況的測試也很重要。測試選擇不當的後果通常與1型錯誤有關,但也可能涉及未能發現組之間的重要差異。多重比較分析測試非常重要,因為儘管ANOVA提供了很多資訊,但它沒有提供有關特定研究組之間差異的詳細資訊,也無法提供有關複雜比較的資訊。這些事後測試的二級分析可能會為研究人員提供該研究的最重要發現。
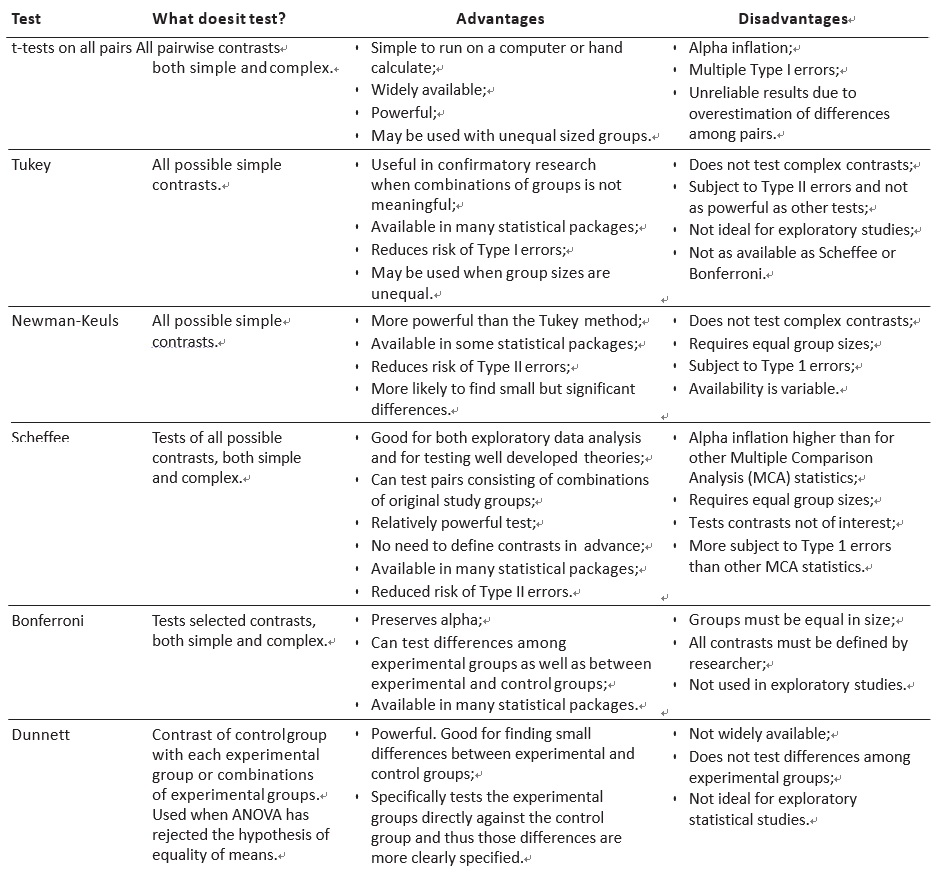
表1.不同多重比較分析統計數據的比較。
TABLE 1. Comparison of different multiple comparison analysis
statistics.
|