|
Title: Errors and Power in
Hypothesis Testing
Source: James H. Wart and
Sjef van den Berg. 2002. Chapter 12. Test Hypothesis.
On
〞Research
methods for communication science.〞
在統計檢定中,如果設定Z值統計量為2.36,數據計算所得Z值大於2.36,因此拒絕了虛無假設。所得結論是〞此虛無假設可能是偽〞,〞對立假設可能為真〞。在此要強調可能為偽,可能為真。因為研究人員無法完全確定此虛無假設一定是真實假設。
為何研究者永遠無法確定,因為在虛無假設與對立假設的對立中,有可能出現兩個誤差,此誤差伴隨著2個正確的歸納結果。
下表列出此結果
|
|
真實情況 |
|
虛無假設為真 |
虛無假設為偽 |
|
研究者結論 |
虛無為真 |
正確
無相關,1-α |
錯誤
第二型β錯誤 |
|
虛無為偽 |
錯誤
第一型α錯誤 |
正確,相關
檢定力1-β |
一、第一型錯誤與正確結論不相關
正確地接受其機率或是拒絕虛無假設的機率是基於常態分佈曲線之面積與虛無假設樣本分佈相關。這個分佈曲線中間點為虛無假設的期望值。其分佈來自樣本分佈的標準差,而標準差由樣本數目與原始數據之分佈狀態決定,(s
= 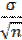 ) ,其分佈曲線為圖12-7之左邊。
) ,其分佈曲線為圖12-7之左邊。
如果研究人員拒絕虛無假設,但是事實上這是一個真實的假設,那就犯下第一型Type
Ⅰ錯誤。研究人員作出錯誤的結論,將對立假設視為真實。例如y與x實際上不相關而將此視為相關。
犯下第一型錯誤的機率由拒絕區域之大小而定。如圖12-7所示,稱為Alpha
error, α。 通常此機率以顯著水準(the
level of significance)表示,例如p=0.05。此顯著水準是用以表示第一型錯誤之機率。
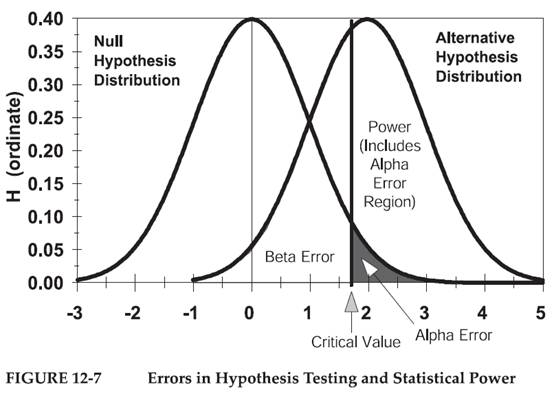
自樣本統計量找到一個數值,而且落在拒絕區域之範圍,這算是一種機率事件,因此此樣本統計量用以顯示虛無假設是錯誤之機率。在虛無假設是真實,樣本統計量還是有可能落於拒絕區域。這個試驗發生機率等於在拒絕之面積,也是第一型錯誤之機率。此拒絕區域面積很大,研究人員拒絕虛無假設的機率也會很大,犯第一型錯誤之機率也會大。比較圖12-7,12-8即可發現。
樣本分佈其中心值即是虛無假設之期望值,臨界值(critical
value)與此中心值距離愈遠,樣本統計所得臨界量(critical
magnitude)發生的機率就愈低。減低拒絕區域面積(例如自0.5降低至0.25),虛無假設愈難拒絕,犯第一型錯誤之機率也是愈低。作出正確判斷的機率為1-α。但是增加(1-α)對於第二型錯誤機率反而增加。
二、第二型錯誤與統計檢定力
正確探查的機率或是對真實的關係判斷錯誤的機率是基於研究者對樣本分佈的常態分佈曲線,或稱對立假設(alternative
hypothesis)。此分佈曲線的形狀(由標準差影響)與虛無假設之形狀相同,但是其中心點不同,是位於一些非虛無數值(non-null
value)。圖示於圖12-7。
如果研究人員接受H0,但是事實上應該揚棄H0,那就產生第二型錯誤Type-Ⅱ錯誤。研究者錯誤歸納y與x無相關性,但是實際上有相關。研究者錯誤地接受了虛無假設,犯此種錯誤之機率為樣本分佈曲線下臨界值的尾端(圖12-7之Beta
error)。
正確地揚棄虛無假設的機率由非虛無樣本分佈(non-null
sampling distribution)之其他面積。此面積數值為1-β,又稱為檢定力(statistical
power)。代表研究人員自其取樣數據中所得到正確結論之機率。
三、對立假設期望值與效應值影響
對於對立假設如何決定其期望值?虛無假設之期望值通常為與平均值無差異,無相關性等,但是對立假設其期望值並不容易獲得。如果我們都不能確定是否有關係存在,如何建立一個效應值?對研究者而言,有好幾個動機促使他選擇一個期望值。
第一個方法是以最小值之概念。以設定一個有效的效應值(effect
size),例如一家公司平均捐款150美元,至少要有10元差距捐款才是有效考慮,因此研究者的對立假設為160美元。
(附註:代表由實質差異以轉為評估統計差異)
第二個方法是藉由先前研究以設定期望值。例如已有研究報告顯示新產品與新工作之相關性為-0.35。那麼對立假設之相關性必須高於-0.35。
在對立假設之期望值一旦建立,可以以效應值以討論大小誤差。討論誤差(錯誤)時,虛無假設期望值與對立假設期望值之不同,稱為效應值(effect
size)。
四、α與β誤差,效應值與樣本數目
(Alpha and Beta Error,
Effect size, and the Number of observation)
內在的關係存在於α誤差,β誤差,效應值與樣本分配之標準差。改變其中一項因子,即影響了其他因子。
要改變樣本分配的標準差,可由改變樣本數目(N)開始。依中央極限定理,樣本的標準差如下:
s =
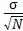
因為母群的分散程度,σ是個常數,與研究人員任何動作均無相關,因此為只有藉由N值以決定樣本分配之離散程度。
α與β值是由研究人員選擇的任意值。通常α的顯著水準經常為5%,代表p
= 0.05。而β值為0.20。這兩個數值無任何依據。只是過去許多研究人員都是如此使用。一個有智慧的研究人員則是依據自己獨特的研究情況加以設定α與β值。
舉例一項針對心臟疾病研究。一個樣本群是離開醫院後,醫院持續給予有關飲食、運動與定期檢查之指示資料。另一個樣本群則是沒有。研究人員探討這種資料提供是否對心臟病有幫助,因此其誤差必須相當小。此研究中Type
Ⅰ誤差(無效但被歸納有效)與Type
Ⅱ誤差(真正是有效,但被歸納無效)相比,TypeⅡ之代價比TypeⅠ更大。
效應值是由研究研究人員決定(例如心臟病到底減少%?)。觀察數目N也由研究人員決定。N愈小,研究工作之成本與時間愈少。因而研究者必須在N,效應值(effect
size),α,β四者中得到一個平衡。
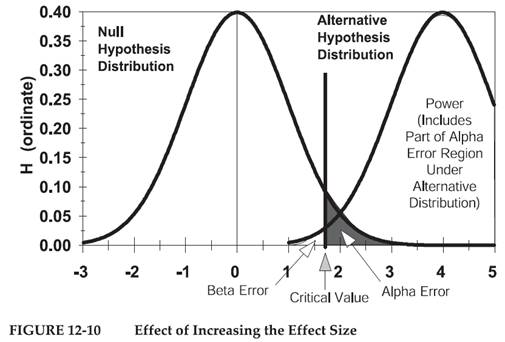
圖12-8代表增加α值之影響,圖12-9代表增加N的影響,圖12-10代表增大效應值之影響。
圖12-8代表增加顯著水準α,使得判斷之臨界值更接近虛無假設之期望值。α增加,拒絕區域面積增加,TypeⅠ之錯誤也會增加,但是TypeⅡ誤差則相對減少。這即是TypeⅠ與TypeⅡ之相對性。在其他條件維持不變時,降低α值(TypeⅠ錯誤)即是增加β值(TypeⅡ錯誤)。
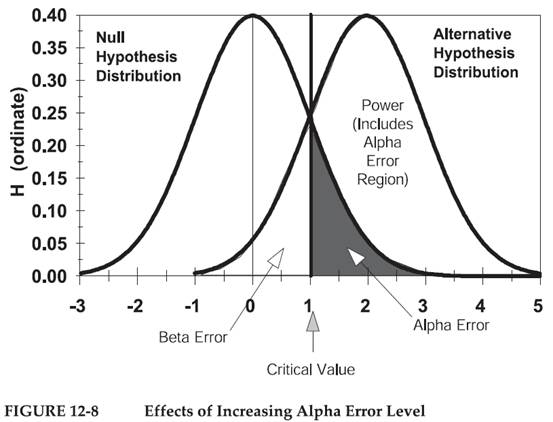
圖12-9代表增加N之影響。有更多的試驗樣本,樣本分佈標準差降低。在相同的臨界標準下,α與β的誤差或然率都降低。在α維持相同信賴水準時,β之機率顯著地降低。N的增加是降低誤差的最佳方式,但是往往增加試驗成本。

圖12-10代表增加效應值,可降低β錯誤,而不需要增加α,也不增加N值。但是增加效應值也有其代價。因為增加了研究假設值與虛無假設值的差異值,研究假設樣本分佈的中心位置向右移動,β值減少。研究結果得到顯著差異的機會也降低。
五、檢定力分析(power
analysis)
因為α,β,效應值與N等四者彼此相關。因此以檢定力分析以說明
Zβ
= 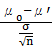
Zdiff =
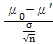
N =

使用檢定力分析最大的用途是決定試驗的觀測數目。如果樣本的數目太少,樣本分佈的標準差則變大,α與β的誤差則相對增加。如果樣本收集數量太大,時間與經費則浪費太多。
要決定試驗數目,看先要設定α,β與效應值,在使用計算公式即可算出需要的樣本數量。
以健康諮詢為例,α之顯著水準設定為0.01,代表只有百分之一的機會使得量測的樣本出現在顯著水準之外。再來將β誤差水準設定為0.05,檢定力為0.95。而效應至少要有10%之差異性。
樣本的標準差以文獻得知為50%,由查表可知α=0.01,β=0.05之情況下,Zβ-Zα=Zdiff=3.971。因此
N=
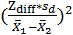 = = =394 =394
因此需要394個以上的觀察量。
另一個檢定力的應用在於檢討未能拒絕一項虛無假設之原因。通常此種失敗的原因有兩種:1.
關係係真正不存在;2.
研究人員採用的統計檢定力(1-β)不足以偵測此相關。
例如上述相關係數之檢定,原來基準 r =
-0.36,試驗結果r =
-0.44,但是統計檢定並未顯示兩者相關。此中有兩項原因:1.
兩者真正無相關;2.
樣本數目太少,因此影響了檢定結果。在此檢定中,α=
0.05,N
= 8,效應大小為0.44。代入計算公式,檢定力(1-β)只有10%。代表第二型β錯誤差高達90%。
|