|
篇名:Ten
common and dangerous statistical mistakes
作者:Ross
Farrelly
Minitab Australia
一、
信賴區間重置之錯誤解釋
兩組數據,其95%信賴區間如果有重置,在95%信賴水準之下兩組數據有可能顯著不同,因此不能由圖直接判斷。
1.
兩組數據其平均值顯著不同:
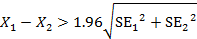 ,但是 ,但是
2.
兩組數據其信賴區間的分佈無重疊:
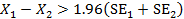
二、
統計上顯著與實質上顯著並不相同
以穀粒盒為例,每一盒榖粒在自動裝填之後,以自動稱重設備量測重量。在18000盆中,其重量的標準偏差為2.5
g。每盆之預定充填量為360
g,以90%之標準,代表偏差0.06
g。以統計原理此0.06
g數量並不適當,以信賴區間判別更合乎實際。再使用統計檢定時,要考慮樣本數目之影響。
三、毫無理由地認定非常態分佈
1.樣本數目太小,以此判別常態分配固而不合理。因此樣本數目不大時,要使用機率分佈圖判別,而不是使用直方圖。
2.樣本數目極大時,要考慮上述(二)錯誤:統計顯著與實際顯著之不同。
3.進行迴歸分析之後,常態分配之檢定是以殘差值(residual)而不是以反應值()。
四、
虛無假設(Ho)之問題
以值判別,P值大於0.05只是顯示“無足夠證據在95%信賴水準之下,得到H1之假設”。
例如丟擲硬幣三次
:向上之機率=0.4
:向上之機率≠0.4
以P值大於0.05,代表之證據不足。但是不代表一定成立。
五、
相關性不等於因果性
(Correlation = Causation?)
例1:冰淇淋的銷售量與犯罪量有高度相關。在夏季,兩者都提高。在冬季,兩者都降低。但是兩者無因果關係。
例2:在製造過程中,產品的重量隨著時間變化,而也受到其他變因的影響。在4月至5月,產品重量增加,但是工廠內其他因子也增加,例如每日產量、作業時數、室溫、生產線速度等。因此無法以單一
因子解釋產品的重量為何增加。
六、
只有以值以評估回歸模式
只是代表模式對樣本變異的解釋比例。與無任何相關意義,。
七、
管制圖之說明
產品規格界限與品管控制極限並不相同。
八、
分析變數,每次只針對一項
例如飛機零組件之腐蝕性與飛行小時。只有評估兩者,找不到相關性。但是加上零件位置此變數腐蝕性與飛行小時即有相關。許多變數彼此的交互相關,以一次一變數之分析是無法確定。因此需要進行多變數分析。
九、
自母群進行比例值評估,但是未考慮樣本數目。
以常態分配之統計技術應用於非常態分配之數據。如果數據並非常態分析,需要進行轉換(Transform)或是選用其他分佈。例如Minitab即提供14種分配。 |