|
Title: Common statical mistakes in manuscripts submitted to biomedical
journals
Author: Farrokh Habibzadeh
Sources: European Science Editing, Nov.2013; 39(4):92-94
一、數據分佈
許多投稿稿件都涉及了分析連續式變數，例如年紀、血液pH值、膽固醇指數等。經常的錯誤是將這些變數數據相同處理。許多作者以平均值與標準差進行參數檢定，例如t檢定。然而在執行參數檢定之前，必須判別這些數據是否為常態分布。只有常態分部才可使用平均值與標準差。非常態分佈應以中數。與IQR表示，IQR為interquartile
range， 與 位數之距離。使用t檢定或ANOVA的基本假設為常態分佈。變數如果非常態分佈，應該使用Mann-Whitney
U test
與Kruskal-Wallis。如何判別常態分佈?單ㄧ樣本以Kolmogmrov-Smirnov檢定是最通用的方法。檢定常態分佈有一簡單法，如果標準差大於二分之ㄧ平均值，此變數即不是常態分佈。
二、標準差與標準偏差
最常見的錯誤是使用標準偏差(the
standard error of the mean, SEM)取代標準差(Standard
deviation, SD)以表示數據的離散程序。SEM一定是小於SD值，因為SD值除以樣本數目的平方根等於SEM。
在一項試驗中，量測225成年男子的血糖濃度，平均值為90
mg/dL，標準差為15mg/dL。數據分佈為常態分佈，因此95%的樣本(214個成人，225人*0.95)其血糖濃度為60(90-15*2)與120(90+15*2)之間。假設這些樣本能夠代表族群，因而95%之成年男子，其血糖濃度為60-120之間。
如果樣本人數為900人，其平均值與標準差為90
mg/dL與15
mg/dL。上述之結果，95%之族群其血糖濃度仍是60-120
mg/dL。
如果以上述225個樣本，進行100次重覆試驗，因此可得到100個平均值與100個標準差。100個平均值不見得完全相同，而100個平均值的平均值即有可能即是族群真正的平均值。然而100個SD之偏差有多少，以SEM即可估計，而不需要真正執行100試驗。
例如
225個樣本，其SEM
=  =
=
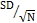0.1
mg/dL
900個樣本，其SEM=
 =
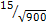0.5
mg/dL
無論原來變數之分配是什麼樣本之分布是常態。因此平均值95%的信賴區間是以平均值±2倍標準偏差加以估算。225個樣本其平均值之信賴區間為98(100-2*1)-102(100+2*1)
mg/dL。900個樣本其平均值之信賴區間為99-101
mg/dL。因此以900個樣本，其平均值比225個樣本之平均值更為精確(Precision)。
SEM不是用以表示量測變數的離散程度。是用以表示樣本平均值的精確性。在科學論文，要使用SD表示數據的分散程度。
標準差不只是可比自樣本平均值加以計算。其他的統計量(Statistics)，例如odds
ratio(OR)，relative
risk與percentage也可計算SD值。
95%信賴區間可由SD值計算，論文採用95%信賴區間之主因是因為可以以圖形表示。
三、不適當的報導統計量的精確性
論文中各統計量之精確度要依據量測值之意義。舉例，在成人樣本之研究有記載樣本，對於年齡之數據與血液pH值之數據不同。後者量測至小數點3位。但是現有的統計軟體依據內建設定加以計算。因此在論文報導中有“年齡平均值97.351年，pH平均值7.123”，其中年齡表示至第三位並無意義，以37或37.4年即可。
另一種常常錯誤的表達方式是百分比。例如35個參預樣本有12人(34.29%)得到感冒。正確的報導是34%。因為增加或減少一個樣本，即代表3%之變化，因此0.29毫無意義。因此樣本數目在少於100以下，報導百分比至1%即可。例如信賴區間之報導，35個參預者，12人感冒(34%；95CI：18-51%)。
四、
在許多論文，值的報導例如>0.05，。許多學者認為值應該以確實數字加以表示，例如=0.0223，=0.647。有的值非常小(例如0.00001)，電腦軟體只顯示“0.000”，結果作者表達的形式竟然是=0.000或<0.000。正確的報導方式應該是<0.000。對於值數據，小數點後三位即是足夠。
五、95%信賴區間或是值
許多論文同時表現值與95%信賴區間(95%CI)，例如“A
was significantly (=0.04)
associated with a higher incidence of (OR=2.6；95%CI：1.3-5.3)。值只是一種機率的表達，樣本的數目都會影響值。但是95%(I不僅告知有效的數字大小，而且告知此差異是否有顯著之不同。例如95%CI代表在95%機率，OR有顯著影響，上述報導如下即可”A
was associated with higher incidence of B(OR=2.6；95%CI：1.3-5.2)。
有些論文報導出相互矛盾之結果，例如OR=3.1；95%(CI：0.97-9.91,<0.05)或是OR=4.3；95%(CI：1.2-16.51,
=0.06)。
六、最小樣本數目之計算
許多論文報導樣本數目，但是並未提供最小數目之計算方式，比較兩種表達方式：
1.
Our hypothesis in that drug X in better than drug Y for reduction
of low-back pain.
2.
Compared to drug Y, drug X can reduce, by at least 20%, the pain
score of women with mechanical low-back pain, as measured by the visual
analog scale.
在第二2個描述，有研究族群(Women
with mechanical low-back pain)，有結果(drop
in pain score)，有量測值(by
visual analog scale)，有期待值(effected
effect size, 20%)
另一個問題是不正確的樣本數目，因此無法區別臨診顯著(clinical
significate)或是統計顯著(statistical
significate)。統計顯著不見得有臨診意義。例如處理組的膽固醇(189
mg/dL)高於控制群的膽固醇(187
mg/dL)，=0.031。對人體健康而言，此統計顯著並無意義。 |
