|
Tom Lang先生為一名"統計技術更正專家",其學術專長不是在大學教授統計學,而是擔任一項自由業,協助研究人員更正其研究論文中所誤用的統計技術。自2003年至2006年,Tom
Lang先生在AMWA
Journal依序發表7篇文章,其標題都是"Common
Statistical Errors Even You Can Find",子標題則是不同。7篇文章之子標題名稱,發表時間,期刊,卷數,頁數等列舉如下:
Part 1. :
Errors in descriptive statistics and in interpreting probability
values. AMWA J., 18(2):67-71, 2003.
Part 2. :
Errors in multivariate analysis and in interpreting differences
between groups. AMWA J., 18(3):103-107, 2003.
Part 3. :
Errors in data displays. AMWA J., 19(2):9-11, 2004.
Part 4. :
Errors in correlation and regression analyses. AMWA J.,
20(1):10-11, 2005.
Part 5. :
Errors in reports of diagnostic tests. AMWA J., 20(2):50-51,
2005.
Part 6. :
Errors in research designs. AMWA J., 20(3):112-115, 2005.
Part 7. :
Common errors in conclusions. AMWA J., 21(1):17-18, 2006.
七篇文章共列舉44項常見的統計技術,依其發表之次序,介紹如下:
PartⅠ:
Errors in descriptive statistics and in interpreting probability values.
No.1. 對於量測的變數未加以定義
研究人員在研究論文內容要交待量測對象,一般稱為變數(Variable),對於每一個變數加以定義,而且說明如何進行量測。例如一個量測變數名為血壓高之樣本,就必須定義血壓量測值是140
mmHg以上,即是高血壓,對過胖症而言,男性體指數要高於27.8,女性要高於27.3。
涉及概念或行為則更難以定義與量測。以美國的抽菸行為的調查研究,"現在正在抽菸者",其定義為接受調查的前30天以內,至少抽了一根香煙。無論此定義是否合理,研究人員必須在此定義之下進行量測。
No.2. 對於每一變數未提供其層次
對量測的變數而言,量測層次(Level)代表收集資訊之多寡。通常對於量測資訊區分成三個層次,"名目(nominal),
順序(ordinal)與連續(continuous)"。
名目(nominal
data)的層次最低,通常包括名稱,分類,而且無高低之次序。例如血型區分成四種:A,
B, AB, O。此種資訊即是名目資訊。
順序(ordinal
data)包括一個內在的次序,可以以階層分別。例如人的身高分類成矮,中等,高。"高"的定義是多少公分以上未註明,但是一個屬於"高"的男人,其身高一定高於屬於"中等"的男人。
連續(continuous
data)代表此變數的數據有其連續性,例如身高單位為163.cm,血壓量測為110.1mmHg。連續性的數據是所有量測變數中最高的層級。
研究人員對於每一個量測變數需要定出其層級。以血壓而言,可以為名目(nominal)層級(高血壓,正常血壓),順序(ordinal)層級(hypotensive,
normotensive, hypertensive),或是連續(continuous)層級(以mmHg表示)。不同的層級,使用之統計技術也不相同。
No.3. 將連續(continuous
data)區隔成順序(Ordinal
data),但未說明如何區分。
為了便於分析數據,連續性數據往往被區分成為兩個以上的順序層級,例如小,中,大。量測的層級降低也代表降低量測值的精密性。研究論文的作者必須解釋為什麼要以順序層次而降低數據的精密性。而且也要解釋此種區分邊界值的依據。
No.4.
連續的分佈非常態分佈,使用平均值與標準差以描述連續性數據。
名目與順序數據通常以數目計算或是比例加以處理,連續性的數據則以圖示以顯示其分佈狀態。數據分佈狀態經常以其統計量加以描述,例如平均值,中數,眾數,範圍,四分之一位數,四分之三位數,標準差等。
上述的統計量都可以用以描述常態分佈,而平均值與標準差是最常用的統計量。事實上只有在常態分佈之狀態下,平均值與標準差才適合使用。
非常態分佈或是偏斜(Skewed)分佈,不適合以平均值或標準差加以描述。非常態分佈之數據,以眾數,四分之一,四分之三位數加以描述更為適合。
大多數的生物性數據並非常態分佈。有個簡易方法以判別是否常態分佈。如過標準差大於平均值之半,此數據群則不是常態分佈。
No.5. 使用平均標準差為描述統計量
標準差(SD.
standard deviation)是用以描述常態分佈的統計量,平均標準差(SEM.
mean of standard deviation)是用以母群精密性之估計值。然而SEM值往往被誤用以描述常態分佈。因為SEM值低於SD值,小的數據使得分佈似乎更窄,顯示量測更精密。對一組調查數據其分散程度的表示可以為SD與信賴區間,而不是SEM。
No.6. P值的誤用
以比較兩群數據是否有顯著差異而言,P值只是用以為一種表達方式,表示兩者是否有顯著差異的機率。如果此機率性十分低,例如5%,代表有足夠證據以說明兩群數據具有差異。P值代表數學上的機率,並未有生物性的意義。機率以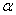 值表示,用以代表檢定統計上的顯著性。P值小於 值表示,用以代表檢定統計上的顯著性。P值小於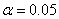 ,代表"統計上的顯著"。P值大於 ,代表"統計上的顯著"。P值大於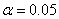 代表"統計上的不顯著"。 代表"統計上的不顯著"。
P值可以協助統計檢定中兩個數據群是否有顯著差異,如果統計上無差異,並不一定是代表兩個數據群是相同。
許多醫學期刊推薦使用"兩個數據群以信賴區間(95%)"以表示其是否差異,而不是只使用P值。以下的三個實例用以說明只使用P值的問題:直接以期刊論文之原文舉例。
1.
The effect of the drug on lowering diastolic blood pressure was
statistically significant (P<.05).
如果P值為0.049,其結論是有顯著差異。而如果P值為0.051,則被解釋為無顯著差異。此研究為藥物降低心臟舒張壓之報導。如果是在P=0.049之情況下,無法說明此結論在醫療行為的實際效用。
2.
The mean diastolic blood pressure of the treatment group dropped
from 110 to 92 mmHg, (P=0.02)。
這種表達方式在研究期刊上經常看到。在此描述中給予使用前後的血壓值。前後的差距為18 mmHg,在統計檢定為顯著,但是此數值也只是藥物是否有效的估計值。沒有信賴區間的數值表示,此種估計方法的精密性無法估計。
3.
The drug lowered diastolic blood pressure by a mean of 18 mmHg,from
110 to 92 mmHg (95%
CI = 2 to 34 mmHg, P=0.02)。
此種信賴區間的數值顯示如果以此藥物針對100個對象進行試驗,對95個對象而言,其血壓降低的平均範圍介於其中2-34
mmHg,降低2
mmHg對治療的意義不大,但是降低34
mmHg則有其重要意義。因此血壓的平均降低值在統計上為顯著。對於醫學治療而言,此種血壓差可能不算是重要。此結果對實際醫療需求而言,無法有實際意義。需要更多的數據以縮短信賴區間再進行判斷。
No.7. 統計檢定的假定條件未加以再驗証
如果統計的假定條件被違背,統計檢定可能得到不真實的結果。因此在進行統計檢定報導時,假設條件都要加以驗証。常見的統計錯誤包括:
1.
使用參數檢定(其前題為常態分佈),而其數據分佈為偏斜分佈
(skewed)。在進行兩組數據檢定時,此問題更加嚴重。數據為常態分佈,t檢定可適用。非常態分佈,則使用Wilcoxon
rank test或其他非參數檢定。
2.
對於成對出現的數據,統計檢定不可採用t檢定,而是要採用成雙檢定
(paired t test)。
3.
使用線性迴歸建立y對x之直線方程式,而未採用殘差圖以檢定是否線性分佈。
No.8. 以統計檢定非顯著結果進行數據解釋
研究者如果發現實驗群之間無顯著差異,他必須考量此種無差異是代表群與群之間相似(similar),或是來自數據不足,因此無法判別是否真正無差異。在進行判別之前,必須進行檢定力計算
(power calculation)
用以決定要使用多少實驗樣本以進行研究,而有多少機率以探查其差異性。許多研究者並未曾考慮檢定力計算
(power calculation),因此無法做出正確結論。
No.9. 對多重假設檢定未報導如何執行
許多研究報告,同時使用不同的P值。但是此種檢定方法也增加了typeⅠerrors。例如實驗共有6組,以每對相互比較其差異是否顯著,至少需要15次,以15次P值進行檢定。以95%之信賴水準,其typeⅠerrors高達55%。
許多情況需要使用多重檢定。直接以醫學論文常用之文句敘述如下:
1.
Establishing group equivalence by
testing each of several baseline characteristics for differences between
groups (hoping to find none).
2.
Performing multiple pair-wise
comparisons, which occurs when three or more groups of data are compared
two at a time in separate analyses.
3.
Testing multiple endpoints that are
influenced by the same set of explanatory variables.
4.
Performing secondary analyses of
relationships observed during the study but not identified in the
original study design.
5.
Performing subgroup analyses not
planned in the original study.
6.
Performing interim analyses of
accumulating data (one or more endpoints measured at several different
times).
7.
Comparing groups at multiple time
points with a series of individual group comparisons (repeated measures
procedures)
No.10. 統計的顯著性與生物的特性互相混淆
許多研究者以P值的顯著性做為生物上的重要結果。實際P值對生物學理無任何相關聯。在判斷生物特性,要同時留意生物的樣本數目與生物自然狀態。以一個諷刺性評論加以說明:"一個人的右腳放在0℃的冰水,左腿放在80℃的沸水,以平均值的觀念而言,這個平均溫度對人體而言是十分舒適。" |