|
Part 2 : Errors in
multivariate analyses and in interpreting differences
一、多變方分析介紹。
在醫學上最常使用的多變方分析統計技術為迴規歸分析與變方分析(ANOVA)。兩者都是用以處理二至三個以上的變數。通常ANOVA主要用以分類變數(categorical
variables)。迴歸分析主要用於連續變數(categorical
variables)。如果一項研究包含了分類變數,連續變數與解釋變數(explanatory
variables),則可使用多重迴歸分析與共變方分析(analysis
of covariance, ANOVA)。多變方分析最主要之步驟是尋找數學模式以解釋變數之間的關係。
(一)、
多重迴歸分析
多重迴歸分析主要有三大類型:
1.
線性迴歸
2.
Logistic迴歸
以2個以上的變數用以預測二項式反應變數(例如痊癒,非痊癒)。
3.
Cox proportional hazards迴歸
以2個以上的變數用以預測事件之時間(例如自外科手術至死亡)。
(二)、
多變方分析
多變方分析主要有五大類型。
1.
One-way ANOVA
2.
Two-way ANOVA
3.
Multi-way ANOVA
4.
ANCOVA
5.
Repeated-measure ANOVA
以實例說明以上五類ANOVA之不同。
1.
One-way ANOVA
具有骨質疏鬆症之婦女分成三群進行治療:分別為標準治療法,新型治療法,給予安慰劑。反應變數為骨質之礦物質密度。不同群各有數組以上之量測數據(骨質密度)。以One-way
ANOVA可以比較三種醫療方式對於骨質之礦物質密度是否有顯著不同。
2.
Two-way ANOVA
對上述研究內容增加第二個解釋變數:年齡。共分成四組,30-40歲,41-50歲,51-60歲,61-70歲。因此在此研究有兩類分類變數:醫療方式與年齡。
3.
Multi-way ANOVA
對上述研究增加第三個,或更多的分類變數,例如素食或非素食,抽菸量(每日2根以上,2-5根,6根以上)。因此研究樣本有四大類:醫療方式,年齡,是否素食,吸煙數量。
4.
ANCOVA
針對上述研究,對於骨質疏鬆病之病情再細分成兩大類(嚴重,輕微)。如果要研究醫療方法與年齡對於骨質疏鬆症之關係,病情程度需要控制。因此對於病情程度再分成三類(輕微,中等,嚴重)。此種分析方法稱為ANCOVA。
除了上述4種ANOVA技術,第5種稱為Repeated-measure
ANOVA。對於相同樣本於不同狀態下進行成對或重覆性量測。例如對病人於仰臥,坐,站等三姿勢下量測血壓,或是手術後1,5,10,20天進行肌肉力量量測。以上述骨質疏鬆病之婦女為例,在治療後的0,6,12個月後進行骨質密度量測。此"時間"影響為ANOVA
model的新變數。其統計技術即為Repeated-measure
ANOVA。
在醫學研究,關於多變方分析常見的錯誤介紹如下:
No.11. 進行ANOVA,但是對ANOVA之假設條件未加驗證
進行ANOVA分析的假設條件是每一變數內量測值都是常態分佈,每一解釋變數之差異量都近乎相同。然而許多生物性的數據都並不是常態分佈,數據需要數學轉換使其近於常態分佈。否則就必須採用非參數分析。例如偏斜(skewed)分佈之數據可使用Wilcoxon
rank-sum test取代One-way
ANOVA。或是以Kruskal-Wallis
test代替Multi-way
ANOVA。
No.12. ANOVA執行完成後,對於使用的多重比較方法未加以註明
以ANOVA進行分析,如果發現處理與處理之間有顯著差異,隨即進行多重比較,以檢定是那個處理與其他處理有顯著不同。使用的多重比較方法必須註明,例如Tukey’s法,Studest-Neuman-Keuls法,Scheffe’s法,Fisher’s
Least-significant法。
No.13. 對於解釋變數未進行交互效應或是重合性檢定
兩個變數(X1與X2)如果有交互效應存在,代表解釋的模式中X1*X2變數存在。交互效應暗示兩個因子必須同時考量。例如血液中酒精濃度與巴必妥酸塩濃度對於致死程度即是相互效應。
兩個變數如果對於模式提供相同的知識,代表兩變數有重合性,例如心臟的收縮壓與舒張壓。
一個研究其內容如果包括大量變數,一定要檢定這些變數是否有交互效應與重合性。
No.14. 數據對於模式的符合性並未報導
符合性(Goodness-of-fit)代表在數據中呈現的模式符合程度。殘差圖檢查最能代表數據與模式是否符合。
No.15. 模式是否有效或是如何有效並未報導
多變方的迴歸模式必須以數據驗証其有效性與預測能力。第一種方法是以70%的數據建立模式,30%的數據以驗証其預測能力。第二種方法為一次移走一個數據,以其餘數據建立模式,再以移出數據驗証預測能力。有些統計教科書以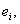 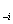 , ,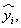 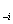 表示。在化學計量學稱為jack-knife法。 表示。在化學計量學稱為jack-knife法。
No.16.
對估計值的信賴區間並未報導
進行統計檢定用以表示是否有顯著不同,差異性的大小與方向都必須評估,才能顯示其臨床差異性。因為實際對象是針對有興趣的母群進行樣本抽樣,並不是對於母群中的全部樣本進行普查。因此統計檢定的結果只是差異性的估計值。在評估差異性時,必須考慮差異性的估計精確度(the
precision of estimate)。
在臨床研究最慣為使用於估計值的精確性是95%的信賴區間,只有顯示估計值容易引起誤解。許多科學期刊要求報導差異質之95%信賴區間,而不是只報告兩處理的差異質。除此之外,也要報導差異值為P值。
最典型的報導如下:
"The
mean diastolic blood pressure of the treatment group dropped from 110 to
92 mmHg (P=0.02)"。
此敘述代表平均差異有18
mmHg之不同,也報導95%信賴區間,但是估計值的精密性並未報導。
另一種更詳細的報導方式如下:
"The
drug lowered diastolic blood pressure by a mean of 18 mmHg, from 110 to
92 mmHg (95%=2
to 34 mmHg,
P=0.02)"。
No.17. 只有報導相對的差異值,而未報導絕對差異值
兩個族群絕對的差異值只是數學上數值的不同。相對的差異值則以百分比表示。以相對的差異值容易導致誤解。例如50%的存活率可以來自2
/ 4之病人比例或是2000
/ 4000病人之比例。以絕對值而言,兩者樣本數值各為4與4000。因此雖然絕對比例值相同,2
/ 4之數目則因樣本數目太少而失去意義。
在科學論文,比例值的分子與分母都應該列舉。因此才能顯示絕對數值。尤其樣本數目低於100,更需要清楚表示。典型的報導舉例如下:
"In
the Helsinki study of hyper. men, after 5 years, 84 of 2030 patients on
placebo (4.1%)
had heart attacks, where only 56 of 2051 men treated with gemfibroil
(2.7%)
had heart attacks (P<0.02)"。
No.18. 樣本的數據並未一一檢視
以三次的臨床醫療為例。第一次醫療中,患病之樣本經治療後自6人減為5人,第二次自4人減為2人。第三次卻自2人增為8人。如果未加檢視三次醫療行為是否有差別,只是以平均值計算治療行為之有效性。治療前病人數目平均值為(6+4+2)/3
= 4,治療後數目平均值為(5+2+8)
/ 3 = 5。第三次醫療行為的影響性在平均值計算中被忽視。
No.19. Post-hoc Analyses與Plannet
Analyses未加以區分
Post-hoc Analyses是在數據分析之後再加以進行。在數據分析之前,對於數據收集未有計劃性。Plannet
Analyses是預先規劃試驗內容。Post-hoc
Analyses需要更嚴謹的判別標準,而且數據數目要更多。 |