|
Title : Use and Misuse of the
P-value
Author : Emmanuel Lesaffre
Source : Bulletin of the NYU
Hospital for Joint Disease, 66(2):146-149, 2008.
此篇精采的文章並不是醫學期刊內的評論(Review),而是美國紐約大學附設醫學院所編輯的期刊。作者身份為荷蘭鹿特丹Erasmus
Medical Center的生物統計學家。
在許多醫學研究中,P值是最普遍用以歸納結論的工具。雖然P值的使用如此普及,其基本原理很少被瞭解,因此在醫學文獻中經常被誤用。在此篇文章,以一個實例的醫學研究案例進行討論。此項研究為兩種隨機而且雙盲的臨床試驗,對照組給予安慰劑(PL)。第一種處理為etoricoxib
30mg qd (ET),第二種處理為COX-2抗化劑配合celecoxib
200mg qd (CE)。研究期間為12週,對象為患有髕關節炎與膝關節炎的對象。559個對象隨機分成三組:PL,ET與CE。在第二個研究中,病人有608人。治療效果以三個方式加以評估:WOMACPA,WOMACPH與PGADs。
一、The P-value與統計試驗
以WOMCPA量測值為例,以EC對PL進行比較。12週的ET處理後,WOMPCA量測值自67.4降至39.6。PL的處理,自66.6降至54.2。以平均值改變量加以比較,ET治療的降低量為27.8。
PL治療的降低量為15.4。ET與PL之差異平均值為-15.07,其P值小於0.001。
假設ET與PL之處理對治療效果相同,真正的差異平均值△為零。如果△=0,可期待研究的結果其數據差異的平均值(DA)值為零。而且只要重複進行試驗,此DA值也都接近為零。然而研究者面對的問題如下:DA值要多大,才能夠顯示ET的治療效果與PL是不相同。為了計算P值,以另一角度討論此問題。如果DA
= 0,那麼DA
= -15.7或是比-15.7更小的機率是多少?在此狀況下,PL與ET的治療效果完全相同的假設稱為虛無假設,以H0
=△=
0代表。在此P
= 0.05代表H0為真實的情況下,DA屬於極端數值的機率(5%)。P
= 0.01則是代表DA為極端數據而H0仍為真的機率(1%)。
P值的計算基於機率條件,而其數據是來自統計檢定方法計算的結果。統計檢定是用以証實虛無假設是正確。如果研究人員希望推翻”PL與EC的治療效果是一樣好”的結論,那就代表對立假設Ha
=△≠0為真。因而必須決定要有多大的DA值,或是多小的P值,才可拒絕H0。習慣上,研究人員採用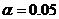 ,稱為顯著水準,這個 ,稱為顯著水準,這個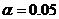 也是進行判定的門檻。應用的方法如下: 也是進行判定的門檻。應用的方法如下:
1.如果P<(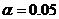 ),如果H0為真,此結果十分極端,發生的機率十分低。因此可以拒絕H0。換言之,我們不相信△=
0,因此在0.05機率下此結果為顯著。 ),如果H0為真,此結果十分極端,發生的機率十分低。因此可以拒絕H0。換言之,我們不相信△=
0,因此在0.05機率下此結果為顯著。
2.如果P≥0.05,代表此結果與H0
=△=
0無極端不同,因雖然觀察的差異值不等於零,但是並未顯示△≠0。因此在0.05顯著水準,兩個方法無顯著不同。
在上述研究中,以WOMACOH量測的數據,ET與CE之數值差異比較,P
= 0.367。因此無法宣稱ET的性能與CE不同。
上述的比較稱為雙尾檢定(△≠0),也有比較△>0或△<0的單尾檢定。除了上述方法,其他的統計檢定包括:
1.成對或非成對t檢定:比較兩組獨立的群組其平均值是否顯著差異,假設條件必須為常態分配,變異數相同。
2.卡方分配檢定:比較兩個獨立群組之比例值。
3.多變方分析:比較兩組以上的群組其平均值之差異。
4.非參數檢定:例如Wilcoxon
test與Kruskal-Wallis test。
統計檢定中基於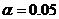 顯著水準,如果P<0.05則拒絕H0。如果H0仍然為真,這種拒絕則是不正確。這種錯誤稱為第一型錯誤(TypeⅠerror)。而H0應該拒絕。兩者真正有顯著差異而未遭拒絕,稱為第二型錯誤(TypeⅡerror)。 顯著水準,如果P<0.05則拒絕H0。如果H0仍然為真,這種拒絕則是不正確。這種錯誤稱為第一型錯誤(TypeⅠerror)。而H0應該拒絕。兩者真正有顯著差異而未遭拒絕,稱為第二型錯誤(TypeⅡerror)。
產生第一型錯誤的機率(TypeⅠerror)稱為false
positive vate,恰好等於 值。此機率可加以控制。第一型錯誤的機率稱為 值。此機率可加以控制。第一型錯誤的機率稱為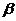 。為了降低 。為了降低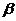 值,樣本數目需要調整。 值,樣本數目需要調整。
二、Misuse of the P-value
A. Multiple Testing
對一個統計檢定以0.05顯著水準,代表拒絕此虛無假設的機率等於0.05。因此H0如果為真,而被加以拒絕的風險為5%。換言之,如果有100個學生進行統計檢定,有5個學生可能錯誤。如果進行多重檢定,則必須控制此種或然率以避免得到錯誤的結論。應用多重檢定的問題舉例如下:
1.有兩種處理,但是有不同的量測值。例如上述兩種處理(ET,PL)進行比較,其量測值各有三種:WOMACPA,WOMACPH,PGADS。
2.兩個以上的處理進行比對,例如上述研究的三種治療方法:ET,CE與PL。
3.兩種處理但是以幾個次組群進行比對。例如上述之各族群再分類成男性,女性,或是65歲以上,65歲以下。只要其中次族群為顯著不同,即代表處理彼此不同。
4.兩個處理在幾個不同的時間點進行比較。
5.使用幾個統計檢定方式以評估兩個處理有否不同。
如果同時進行統計檢定,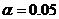 的機率就不是獨立事件。以上述三原理。(ET,CE,PL),相互成對比較共有三項,三個統計檢定不能都以P=0.05為比較標準。為控制此種誤差率,有一種調整方式稱為Benferroni調整,P值之檢定極限值則為0.05/3。詳細理論請參考統計之教科書。 的機率就不是獨立事件。以上述三原理。(ET,CE,PL),相互成對比較共有三項,三個統計檢定不能都以P=0.05為比較標準。為控制此種誤差率,有一種調整方式稱為Benferroni調整,P值之檢定極限值則為0.05/3。詳細理論請參考統計之教科書。
B. Interpretation of a
non-significant result and sample size calculation
如果P值大於0.05,此為非顯著性,因此虛無假設未被拒絕。有些統計檢定宣稱結果為負,代表無顯著不同。但是在增大樣本數目之後,統計檢定結果反而為正,有顯著不同。因此樣本數目也會影響檢定結果。
有句成語如下:缺乏證據並不代表證據缺乏
(absence of evidence is not evidence of absence)。換言之,如何我們無法顯示"差異性",那不代表一定是"無差異"。在此情況下,我們不能宣稱H0為可接受(H0
is accepted),只能宣稱不拒絕H0
(not reject H0)。
在樣本數目太小情況下,第二型錯誤的犯錯機率相對變大。研究者要確定實驗方法,使得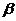 值變小,或是(1- 值變小,或是(1-
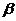 )值變大。除了樣本數目,影響統計檢定正確性的因子有: )值變大。除了樣本數目,影響統計檢定正確性的因子有:
1.試驗效果的量測或評鑑方式
2.統計檢定方法
3.顯著水準
4.臨床相關顯著標準(△S)
C. Statistically significant
versus clinically relevant
統計檢定的顯著結果不代表與臨床治療有相關。例如有兩種藥劑(A與B)用以治療MI病人。以1年之後死亡率為量測值。對2個族群,各為400人,A藥與B藥之治療結果死亡率各為2%(A藥)與10%(B藥)。以卡方分析,P<0.01,代表高度顯著差異性。各以100,000人進行試驗,A藥結果為0.002%,B藥結果為0.001%。以卡方分配檢定,P值亦顯著高度顯著不同。對真正臨床治療而言,A藥對B藥比較無實質意義。此代表樣本數目對統計檢定之重要。
三、95%顯著區間
雖然P值仍為許多醫學研究者用以檢定不同醫療處理是否有顯著差異。但是許多醫學期刊已認知使用P值很難得到有用的解釋。目前例如the
New England Journal of Medicine與The
Lancet,都要求以95%顯著區間confidence
interval(CⅠ)以報導結果。
以上述例如,兩個處理平均值之差異,DA
= -15.07。事實上DA只是一個估計值,對於真正的差異值仍然未知。以95%顯著區間即可表示此種不確定性。換言之,95%CI代表真正差異值(△值)95%機率的出現範圍。如果CI愈窄,代表對△的估計愈佳。以WOMACPA量測值為例,95%CI之報導如下:
1.CE-ET:(
-7.02 , 0.77 )
2.ET-PL:(
-19.72 , -10.41 )
3.CE-PL:(
-16.57 ,
-7.34 )
因此以95%CI進行解釋,比P值更容易理解。例如以第3項檢定而言,CE與PL的真實差異值有95%的機率位於-16.57與-7.34。
P值與95%CI仍然有關係存在。如果95%CI未包括零,代表P值小於0.05。自95%CI顯示CE與ET並無顯著不同,因為其95%CI包括零。
由此可知,95%CI顯示的資訊比單純的P值還多。兩個方法都可用以進行統計檢定。然而CI容易解釋,也可以配合醫學專業進行判斷。 |