英國整型外科研究期刊論文對"無顯著差異"之誤用

中興大學 生物系統工程研究室 陳加忠

此篇論文之出處如下：

Author : SA Sexton, N Ferguson, C. Pearace, DM Ricketls

Dept. of Orthopaedic Surgery, Princess Royal Hospital, West Sussex, UK

Title :  The misuse of "no significant difference" in British orthopaedic literature

Source : Ann R Coll Surg Engl 2008; 90:58-61.

此篇文章的4名作者對關於整型外科的3種研究期刊加以搜尋，發現許多論文已進行統計檢定，而且其結論是"無顯著的差異"，但是這些論文都未曾進行檢驗力分析(Power Analysis)。由於未曾進行檢驗力分析，因此對於"無顯著差異"之結果則難以解釋。

任何治療試驗之實驗程序往往針對以下之影響因子進行統計檢定，例如外科程序，藥物處理，義肢使用或是其他因子等。在進行試驗研究之前，必須進行統計假設。基本的假定是新的方法或新的藥劑之影響結果其母群平均值與對照值(或稱控制組，control)之母群平均值並無顯著差異。另一個對立假設是新的方法或心的藥劑其母群平均值與對照值母群之平均值有所差異。

進行實驗即是自大量母群中抽取樣本進行調查，以樣本之結果代表母群。主要的問題是樣本本身的變異程度是否會導致於錯誤的結論。甚至於採用高標準的試驗設計與試驗，這些試驗樣本還是有微小的機會導致錯誤。其主要原因是因為樣本太少而無法得到正確的結果。換言之，每一個試驗都可能產生第一型(TypeⅠ)與第二型( TypeⅡ)之錯誤。

第一型錯誤：虛無假設(null hypothesis)被拒絕，但是事實上此虛無假設是正確。產生第一型錯誤之機率稱為α，通常以P value稱呼，例如(P＜0.05)。

第二型錯誤：虛無假設是錯誤，但是檢定的結果並沒有拒絕。實際上有顯著差別，而結論竟是無顯著差別。得到第二型錯誤之機率為β。

在理想的研究設計中，α值愈低，則可避免將無差別的結果誤判為有顯著差異。同樣地β值降低，則可避免第二型錯誤。然而α與β值相互關連。在所有條件都不變之下，降低α值則增加β值了。因此要同時降低α與β值的方法是增加樣本數目。為了處理樣本數目，檢定力分析(Power Analysis)則被引入研究界。

檢定力代表在虛無假設為錯誤時，試驗結果能夠拒絕虛無假設之能力。在大多數的外科研究試驗之中，β值通常為0.2或0.1。因此檢定力則是0.8(1-0.2)或是0.9(1-0.1)。換言之，如果不同處理之影響能夠真正的呈現，其呈現的機率是80％或90％。在外科學術期刊常常看到此結論"there is no significant difference between groups"。這個結論的可能意義是對於進行研究的不同處理樣本，其試驗結果無統計性差異(there is no statistically detected difference between the groups in our study)。但是讀者有興趣知道是如下的敘述："is there no clinically significant difference between the groups in the study"。

藉由檢定力分析則可告訴讀者以下兩種敘述之不同：

1.          There is no significant difference between groups

2.          There is no statistically significant detected difference between the groups and our study had on 80％(or 90％) probability of detecting our minimum specified difference in treatment effect.

在醫學研究中，可進行試驗的樣本總是有限。在不增加樣本數目，不改變P值而能增加檢定力的方法有5種：

1.      對於對照組，低風險性，成本低等樣本增加數目。

2.      在比較平均值時降低其標準差。改善標準差的方法包括使用更準確的量測技術，或是組群內的樣本其均勻性更好。

3.      增加對照值之樣本數，尤其是有可能受到影響之樣本。

4.      以連續性的量測方式可減少樣本數目。例如對同樣的樣本進行連續性分數評估因此可減少樣本數目。

5.      避免使用太多的試驗群組。太多的群組使得每組內的樣本數目減少。

最理想的檢驗力分析是有大量的樣本數目，而且有很小的標準差。相反的，一個試驗如果樣本數量小，變異量又大，其試驗檢定結果如果是無顯著差異，對實際研究無多少用途。

上述的原理也適用於信賴區間的計算。如果樣本數目太小，信賴區間之範圍則極大，第二型錯誤就容易產生。

試驗開始執行，就應該使用檢驗力分析。但是研究界對此仍有爭議。如果正確使用，檢驗力分析十分有用。如果使用錯誤，則產生嚴重的問題。例如試驗檢定結果樣本無顯著差異，但是因為檢驗力十分低，其實際結果不見得如此。使用檢驗力計算對研究者可提供一種工具，用以判別其統計檢定之結論"無顯著差異"是否合理。

此篇文章之作者對3種期刊進行調查，其結果如下：

執行檢驗力計算最大的困難在於如果比較之族群不僅於兩群，計算方式更為複雜。

對於檢驗力加以計算，對於統計檢定結果不會造成改變。以乙經完成試驗的觀察值再計算樣本需求數目似乎是無用。但是此數值，檢驗力的大小，可以給予讀者一個參考數值。用以評估第二種錯誤的風險有多大。理想的研究是開始進行試驗即需要評估此檢驗力。

文章之附錄：使用檢驗力分析以計算樣本數目

在兩組數據都是來自常態分佈，在進行t檢定以比較兩組數據平均值是否有顯著差異，其所需樣本數之計算公式如下：所需變數(Variables)必需先預定如下：

1.      α代表P值或是顯著水準，通常為0.05與0.01。

2.      檢定力(1-β)通常為80％或是90％。

3.      E代表關於診斷試驗之最小的有效影響量。

4.      σ為樣本的標準差。

5.      △等於。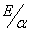

推薦使用之公式為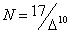：。 此公式之文獻來源為：Dallal GE. 1992. The 17/10 rule for sample size determination. Am Stat, 46 :70。

應用實例：在兩種人工膝蓋之功能比較中，兩種人工關節之差異要求為10度，量測數據標準差為20度，所需要之樣本為：E=10，σ=20，Δ=10/20=0.5

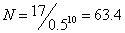
因此在進行試驗時，所需之樣本數目各為64人，共需128人。

在上述的計算個例中，量測數據之基本假設為常態分佈。有關計算所需樣本之基本假設與對樣本數目之影響如下：

1.      如果數據非常態分佈，檢定力將降低。需要更多的樣本數目才能檢查其影響是否顯著。

2.      如果是進行單尾試驗(顯著大於或是顯著小於)，檢定力則是增加，需要的樣本數目降低。但是檢定結果必需與原先的大於或小於方向一致。

3.      成對檢定(paired tets)的檢定力比非成對檢定更高。

4.      如果試驗結果之顯示為類比數據(Categorical data)，檢定力則降低，樣本數目需要增加。

5.      上述實例之差異性為10度，如果差異性為20度，檢定力則是增加，所需樣本數減少。但是E值不能增加太大，否則就失去診斷治療之意義。

6.      改變α值也改變了檢定力，因此P值要避免大於0.05。在有些狀況下，初步試驗可以降低P值，但是樣本數目也會增加。

        如果量測設備的準確性愈差，量測結果的標準差也將是愈差愈大，需要更多的樣本數目。因此量測的準確性與敏感性對決定樣本數目十分重要。