|
此篇文章"Statistical
Methods in Biomedical Research and Measurement Science"發表於斯洛伐克所發行的期刊"Measurement
Science Review"(2005)5:1-10。作者Julia
Volaufora原來任職於斯洛伐克科學院,現今為美國路易斯安那州公衛部門擔任生物統計專家。此篇文章介紹五個生醫研究常常見到的子題:
1.
變異的來源
(Sources of Variability)
量測數據是研究的第一步,要自這些數據進行歸納得到結論,因此統計原理十分重要。對於量測科學,統計學是基本學科。尤其在於量測理論,量測方法,數據與誤差分析,標準與校正等都需要統計學。量測研究中自各種數據來源(量測設備、量測系統、實驗室比對資料等)要進行確認與估計,進行不確定度綜合評估等。而且更進一步推衍一些方法對量測系統進行品質控制程序,信賴性建立等工作都需要統計學。
生醫統計本來就是統計學的一部份。生醫統計關心的主題是進行公共健康與生醫研究的實驗設計與數據分析。在進行生物性的試驗時,科學家必需面對幾種彼此獨立的變異來源。通常實驗設計即是用以比較對照組與試驗組是否有所差異。為了達到此目的,先選擇一些變數(Variables)以進行量測。通常是以一個固定的時間間隔,對相同的變數進行重覆量測。這些量測具有一些變異性,而這也是量測系統中量測誤差的特性。針對試驗對象要得到結論則必須針對一些特定的族群進行觀察。自族群中取出一些樣本進行量測。
為了減低樣本的偏差,必須以隨機方式進行取樣。例如對兩個族群:觀察組與對照組,都是以隨機方式進行觀察。對照組在此作為一個判別標準,一種比較的參考,以判別試驗組的效力。在進行試驗中可以發現至少存在三種可能的變異值。
1.
生物性本身的變異影響。
2.
量測對象因為觀測時間不同對其本身的影響。
3.
由於量測設備產生的量測誤差。
對工程技術而言,其量測結果也具有此三項誤差(系統內個體之誤差、在系統內因時間不同因而相互不同、量測誤差)。在工程研究中,第一種系統內個體的誤差可以忽略,第二種系統內因時間不同的相互不同也不嚴重。但是在生醫研究中,生物體本身變異與組群內量測時間不同影響的變異性反而遠遠高於量測誤差。
2.
混合線性模型-雙維異質性混合模型
為了考慮各種變異來源的影響,首先假設各種觀察對象彼此量測值都是相互獨立。任何一個量測值的影響因子來自樣本本身、處理、時間與重覆性。最簡單的模型:
|
 |
(1) |
 代表在第i組處理群,第j個對象,在第k個時間,第 代表在第i組處理群,第j個對象,在第k個時間,第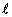 的量測值。μ代表未知的母群平均值, 的量測值。μ代表未知的母群平均值,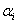 代表第i個處理的固定影響,也是此研究進行量測之對象。 代表第i個處理的固定影響,也是此研究進行量測之對象。 為對象(subjects)之變異,其平均值為零,族群的變異量為 為對象(subjects)之變異,其平均值為零,族群的變異量為 。 。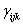 代表族群與處理間之隨機效應,平均值為零,變異量為 代表族群與處理間之隨機效應,平均值為零,變異量為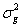 。 。 為量測對象間的隨機效應,平均值為零,變異量為 為量測對象間的隨機效應,平均值為零,變異量為 。 。
如果在每次量測中只有一個量測值(無重覆性),對象中之隨機誤差則為 ,兩者無法加以確定區分。在公式(1)中的隨機變異代表彼此獨立。對一個觀察值 ,兩者無法加以確定區分。在公式(1)中的隨機變異代表彼此獨立。對一個觀察值 而言,其變異量為 而言,其變異量為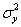 ,因此 ,因此
|
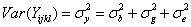 |
(2) |
此公式對所有i,j,k,l皆相同。
對於相同對象,在相同時間點的不同量測值其共變數(covariance)
|
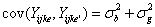 |
(3) |
對所有i,j,k,但是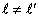 。對相同對象,在不同時間點的共變數: 。對相同對象,在不同時間點的共變數:
|
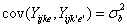 |
(4) |
此對所有數據點 有效。 有效。
對於不同取樣單位的兩個觀察點,其共變數為零。將上述變異值以數學公式表現,包含固定與隨機影響,因此可稱為混合線性模式,或是雙維混合線性模式。
對公式(1)可以進行各種修正。例如在同一時間對同一對象的重覆量測值,為增加其精確性,以減少量測誤差的變異量,對量測值加以平均之後,
|
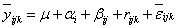 |
(5) |
如果在每一時間點,對所有量測對象之量測重覆數目都是相同(n),公式(5)可修正為:
|
 |
(6) |
上述的混合線性模式是用以估算固定效應(fixed
effects)。但是在實際應用上,只能稱為特殊案例。在醫學研究中涉及對一對象進行多種計算,例如體脂比例,血壓等。但是對Meta分析則不適用。
3.
量測方法之比較
以圖示法比較兩種方法對處理對象是否有相同的量測結果,最常用的方法是J.
M. Bland與D.
G. Altman之論文。
1.
J. M. Bland與D.
G. Altman(1986). Statistical methods for assessing agreement between two
methods of clinical measurement. Lancet, 307-310.
2.
J. M. Bland與D.
G. Altman(1995). Comparing methods of measurement why plotting
difference against standard method is misleading. Lancet, 346,
1085-1087.
在2005年3月為止,上述論文已被引用超過9000次。因為此方法簡單而且一目暸然。
以一篇論文之數據進行比較,108個12歲的兒童,以數種身體成份量測方法進行量測。傳統的量測方式稱為X-ray
energy absorptionmetry (DXA),成本十分昂貴。因此建立另一個簡便方法是使用人體4種成份(密度,水分含量,身高與體重)以計算人體脂肪比例。對每一個兒童而言,各有一個DXA量測值與簡便公式計算值。在圖示方法中,Y座標為由4個成份所計算之體脂比例。X為DXA量測的數值。
此種觀察值之比對模式:
|
 |
(7) |
在此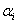 為對象之間的影響值, 為對象之間的影響值,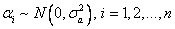 , ,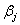 為固定的方法影響, 為固定的方法影響,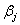 代表每一方法的偏差值,因為只有兩種方法(DXA法與公式計算法),因此j=1,2, 代表每一方法的偏差值,因為只有兩種方法(DXA法與公式計算法),因此j=1,2, 為誤差項, 為誤差項,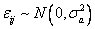 ,代表兩種方法不同的變異數。此模式假設這些變數彼此獨立,而且都是常態分佈。 ,代表兩種方法不同的變異數。此模式假設這些變數彼此獨立,而且都是常態分佈。
如果兩個方法有共同的偏差(bias)與共同變異數(Variance),兩個方法可認為相同。以模式進行兩個方法之比較牽涉其平均值,而此數值受到對象之影響(因為每個小孩都有其體脂值),而且兩個方法本身之量測值也有差異。
為了評估兩個方法是否一致,檢定條件如下:
|
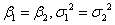 |
(8) |
因為每一個方法只有一個量測值,量測值誤差之變異數無法估算,只能測試是否相同。對於量測誤差之變異數測試其是否相等,其方法在統計學界早已提出。
如果兩個方法其量測值各為Y1與Y2,其相異為Y1-Y2,相同為Y1+Y2,兩者的共變數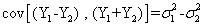
因此將兩個量測方法的差異值對兩者的平均值進行迴歸分析,檢定其迴歸直線的斜率是否為零。如果斜率為零則通過檢定,代表兩個量測值之變異量為相等。
對公式(7)而言,其中一個方法被認為是標準法,通常此標準法的偏差與變異數仍然需要與新方法進行比對。
為了簡化此比對,簡易法如下:
|
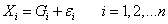 |
(9) |
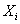 為新方法的量測值,量測誤差為 為新方法的量測值,量測誤差為 ,平均值為零,變異量為 ,平均值為零,變異量為 ,而且與標準法完全獨立。 ,而且與標準法完全獨立。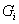 為標準法量測值,其平均值為μ,變異量為 為標準法量測值,其平均值為μ,變異量為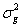 。兩者量測試樣的相關係數: 。兩者量測試樣的相關係數:
|
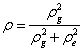 |
(10) |
統計學家對上述方法提出批評,認為此方法並未考慮相對之偏差。適當的方法是以迴歸分析進行斜率與截距的同時檢定。檢定斜率為1.0,截距為0是否同時成立。
4.
檢定偏差與變異量是否相等
如果兩者的方法其量測數目相同,對平均值 與 與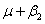 的檢定並不需要估計其變異量。檢定假設為 的檢定並不需要估計其變異量。檢定假設為 ,另一個對立假設 ,另一個對立假設 ,用以進行成對比較。 ,用以進行成對比較。
在此情況下,變異量是否相等,可使用t檢定。以兩量測值之差(y1-
y2)對兩量測值之平均值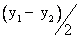 進行迴歸分析,以檢定其斜率是否為零。 進行迴歸分析,以檢定其斜率是否為零。
5.
數個方法之比較:測試偏差是否相等
如果量測方法不只兩種,或是每一方法不僅是一個量測值,可用的模式為:
|
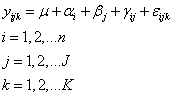 |
(11) |
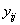 來自方法與不同對象之交互影響。 來自方法與不同對象之交互影響。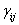 為隨機,常態分配,平均值為零,變異數為 為隨機,常態分配,平均值為零,變異數為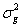 。使用的量測方法有J種,每次量測的重覆數目為K。進行之檢定為 。使用的量測方法有J種,每次量測的重覆數目為K。進行之檢定為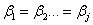 。因為具有J個量測誤差變異數,代表J個量測方法之變異。 。因為具有J個量測誤差變異數,代表J個量測方法之變異。
此多重比較最好使用最大近似法(Maximum
Likelihood method, REML),而以近似F-test進行檢定。有兩篇論文可加以參考引用:
1.
Fai, A.H.T. and P.L. Cornelius (1996). Approximate F-test of
multiple degree of freedom hypothesis in generalized least squares
analyses of unbalanced split-plot experiments. J. Stat. Comput Simul.
54, 363-378.
2.
Kenward, M.G. ard J.H. Roger (1997). Small sample, inference for
fixed effected from restricted maximum likelihood. Biometrics, 53,
983-997. |