|
論文出處:
1.
作者:John
Ludbrook, Dept. of Surgery, The University of Melbourne, Melbourne, Au
2.
篇名:Statistics
in Biomedical Laboratory and Clinical Science: Applications, Issues and
Pitfalls
3.
期刊:Medical
Principles and Practice, 2008; 17:1-13
此篇論文是討論如何結合生醫研究與統計學。與純粹統計學教材或期刊論文有所不同,其中最大的不同在於作者是外科醫生非統計學家。
A.
研究之試驗設計
進行科學研究,代表研究人員有一個想法或有一個疑問。因此為了解決問題,科學家提出一個假設。這個科學假設需要有一個方法以測試。一些研究是依襲以前的方式,新的試驗則必須建立自己的試驗,通常先進行預先試驗(pilot
study)。先期試驗有兩種目的。第一是改善或校正試驗方法,但也可以進行統計作業。現今之研究首先要估計最小的樣本需求量,有時稱為檢定力分析(power
analysis)。因此需要研究者評估所需要進行的試驗數目。最小數量的估算是因為樣本數目必須足夠。在試驗之前,需要研究人員進行初期試驗,用以瞭解進行之試驗與現行的方法是否有顯著的不同。樣本大小的決定是具有雙重目的。一方面樣本數目不能太小,才可避免因樣本代表性不足引起誤差。一方面樣本數目又不能太大,太多的樣本需要龐大的試驗成本。
在進行實驗之前,醫學人員應該與生醫統計專家討論以確定實驗設計。生醫統計專家可以協助修正改良實驗設計以及建議數據分析的最佳方式。無論是臨床或科學試驗,統計專家將協助在兩尾檢定顯著水準(p=0.05)之情況下,接受或拒絕統計假定的需要樣本數目。有經驗的研究人員則可藉由統計表或相關軟體計算結果。
B.
暫時性的統計分析
在實驗進行階段尚未完全結束即進行數據分析,對研究結果的判定是十分危險。研究者應該依據預先決定的樣本數目完成試驗工作。只有在下列兩種情況下,才可以違背此定律,在試驗過程中停止試驗。
1.
系列分析(Sequential
Analysis)
系列分析代表有足夠數量的試驗單位可以在研究過程中抽離,每個試驗單位的試驗時間不能太長。在此種試驗研究中,有兩個邊界值。如果最新的試驗樣本與補充得到的另一對照樣本,顯示在p<0.05的條件下有足夠的顯著性,則顯示兩處理為相異性。如果最新的試驗樣本交叉影響(crosses)另一對照組的邊界值,代表在p>0.05之狀況,兩者有顯著的不同。
2.
數據監視
每一臨床試驗應該有一個委員會進行監督(Data
Monitoring Committee, DMC)。DMC由此研究領域的專家與一位統計學家所組成。DMC的成員與研究者完全無關,在研究過程中一但到達預定階段,統計學家的功能是對DMC分析其數據,是否表現出對照組與試驗組有那些不成比例之數據,而且根據這些結果顯示兩處理有顯著的差異。DMC可建議研究人員終止試驗或是統計專家以此建議研究人員重新估計所需的最小樣本數目。如果樣本數目超過估計值,DMC對研究者重提建議,例如採用更多的樣本,或是因為可試驗之樣本數目太少而放棄此研究。
C.
試驗結果的統計分析
研究人員在進行假設檢定之前,必須決定使用的檢定技術。第一步驟是整理數據,使其合乎檢定之需要。首先將連續性的數據以散佈圖加以表示。分類性(categorical)數據以表格或頻率圖表示。檢查數據的第一步是檢視是否有遺失的數據或是偏離太大的數據。
1.
遺失之數據
在Excel表中,遺失的數據以空白欄表示。研究人員必須檢視為何有遺失之數據。在臨床試驗中,可能是病人在診療過程中不再接受治療。
研究人員在追涉遺失的數據之後,要決定如何處理。有些數據是因為儀器損壞,觀察人員的失誤,或是實驗動物無預期的死亡。有時在兩組或多組獨立試驗組群中,遺失的數據只是一個微小的干擾。但是在長期時間性(longitudinal)研究中,例如採用RM-ANOVA(Repeated-measures
analysis of variance),遺失數據可能導致大的失誤。對Two-way或multi-way
ANOVA,其影響則不大。
如果遺失的數據對統計分析有極大的影響,有個方法可填補此數據。對樣本數目不大的數據群,對人員進行計算即可進行此動作。但是對大量數據,遺失數據可能高達10%至20%,則需要以電腦軟體以計算補充數據。
2.
離群組(Outlying)之觀察
通常認為離群組可以以X-Y散佈圖加以觀察。但是有關生物性的調查數據往往並不是常態分布,需要進行轉換。可用的轉換為對數轉換。離群值在經過對數轉換之後,則不見得是離群值。
另一種對付離群值的方法稱為修整法(trimming),將數據群中最小與最大值之10%加以刪除。
3.
選擇最佳的統計程序
目前已有許多商業化的統計軟體,但是如果統計方法不正確,使用商業軟體也無法得到正確答案。
自R.A.
Fisher’s的學說提出之後,顯著性測定是與p值比較。p值代表對立假設為真的機率。但是二十幾年來,信賴區間也被採用為另一種評估技術,通常採用95%信賴區間。
在執行顯著性比較時,必須考慮第一型與第二型錯誤。此兩種錯誤在統計學教科書可找到詳細資料。
4.
多重比較的問題
如果只有比較兩組數據,以單一p值為標準並無問題。但是如果執行多重檢定,以p=0.05為基準就容易產生許多問題。以一個實例說明多重比較值,判別之p值其數值的不同。以下四處理以ANOVA檢定顯示
|
表1.
四處理之ANOVA分析有顯著差異 |
|
|
組群 |
|
處理 |
|
數目 |
|
平均血壓 |
|
|
|
A |
|
Placcbo |
|
4 |
|
116±1.8 |
|
|
|
B |
|
B-blocker |
|
4 |
|
106±1.3 |
|
|
|
C |
|
Diuretic |
|
5 |
|
104±1.5 |
|
|
|
D |
|
B-blockert + Diuretic |
|
5 |
|
90±1.5 |
|
|
|
|
|
與A組進行成對比較之結果 |
|
|
|
|
|
比較 |
|
未修正之p值 |
|
以Dunnett法修正p值 |
|
|
|
A vs B |
|
0.121 |
|
0.270 |
|
|
|
A vs C |
|
0.021 |
|
0.052 |
|
|
|
A vs D |
|
<0.001 |
|
<0.001 |
|
5.
取樣方法與統計歸納方法
在古典的統計理論中,樣本是來自母群的大量任意數據。這種取樣稱為自族群均勻不偏取樣。
在生醫研究中,研究者對於樣本分成兩組或更多組,分別給予不同的處理。
在統計檢定時,對連續性數據進行t檢定,對分類型數據進行χ2檢定。但是樣本數不大,數據非常態分佈之情況下要另行處理,通常為非參數統計法。
D.
通用線性模式(The
general linear model)
大多數的統計理論其基礎是來自連續性的數據,包括t檢定,各種型式的ANOVA與線性迴歸分析。這些統計技術基於三種假設:
a.
自一定的族群進行隨機抽樣。
b.
這些族群是常態分佈,或者至少是對稱分佈。
c.
這些族群的變異數是相同(相等)。
第a個假設在醫學研究上難以檢驗,但是可以忽略。第b假設則不是十分重要。由Monte
Carlo模擬研究顯示ANOVA方法對於不是十分合乎常態之分佈仍然可以適用。然而假設c則是十分重要。如果兩個族群的變異數其倍率是2或3,對t檢定與ANOVA造成極大傷害。
通用線性模式的一些方程式列舉如下:
在這些公式中,a,bi代表迴歸係數。
公式(1)可用以One-way
ANOVA。公式(2)為multi-ANOVA與多重迴歸分析。公式(3)為two-way
ANOVA與交互效應。
1.
兩個平均值之比較
這種統計檢定通常採用t檢定或One-way
ANOVA。以兩組數據加以比較(表2)。未經轉換之數據,其p值為0.049,代表有顯著差異。經過對數轉換之後,P值為0.052,代表無顯著差異。如果以非參數統計法進行檢定,Wilcoxon-Mann-Whitney程序的檢定結果p=0.072代表不顯著。但是以此非參數統計法是否適用此檢定?因此在無其他證據之情況下,不建議採用非參數檢定。相關的數據如表2。
2.
多組平均值之比較
此種檢定在傳統上採用ANOVA。進行此種檢定其基本前提在於各處理必須相互獨立。如果檢定結果為有顯著差異,可以以Post
hoc Paired contrast法進行成對比較。Dunnett’s法適用於以一個控制組群與其他組群比較。Tukey-Kramer法適用於所有可能的成對比較。
3.
許多相關組群其平均值之比較
對於two-way或multi
way ANOVA即適用此情況。其結果包括主要效應與交互效應。
4.
一系列觀察值其平均值之比較
此種實驗設計在於一組或數組樣本置放於不同的情況下,在一系列的時間間隔下進行調查。以一典型的例證說明此種比較。使用的統計方法稱為Greenhouse-Geisser與Huynh
Feldt。圖1與表3顯示RM-ANOVA之結果。對於doze與處理之相互影響,其p=0.0156。顯示無交互影響。
E.
其他與醫學研究相關的統計分析
針對比例或頻率之分析,常用方法列舉如下。這些方法都可以在統計教科書找到詳細說明,
1.
Tables of Independent Frequencies.
2.
Tables of Related Frequencies.
3.
Tests for Trends.
4.
Binomial Logistic Regression Analysis.
5.
Survival Analysis.
F.
研究報告中有關統計方法與結果之描述
在發表研究論文時,有關統計分析之方法與結果,其程序如下:
1.
在方法(method)章節寫下使用之統計方法。為什麼選擇這些方法,這些方法能得到那些結論。
2.
說明使用的統計軟體,版本,出版商例如:SPSS
V.14 (SPSS Inc., Chicago IL.,USA)。
3.
將統計分析的結果與相關數據以圖表表示。
4.
將名詞加以定義,例如n(樣本數目),p(虛無假設之機率),95%
CI(信賴區間),s(標準差),r(相關係數)等。
5.
對於統計註解加以描述,例如平均值±標準差(Meau±standard
error),平均值±標準偏差(Meau±standard
deviation )。對於顯著水準加以定義。例如雙尾p≦0.05。
6.
儘可能將p值加以表格化或是在圖形說明(Legends)加以註明。p值要以數值表示,例如:p=0.13,或p<0.001,或P
always>0.07。避免使用以下的表式方法p<0.05
或NS(not
significant)。
|
表2.
Outcomes of analyzing the data |
|
a. Descriptive statistics |
|
Data set |
n1 |
n2 |
 |
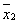 |
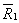 |
 |
SE1 |
SE2 |
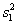 |
 |
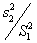 |
|
Raw |
10 |
10 |
14.2 |
15.4 |
8.2 |
12.8 |
0.31 |
0.52 |
0.99 |
2.68 |
2.71 |
|
log10 |
10 |
10 |
1.15 |
1.19 |
8.2 |
12.8 |
0.03 |
0.04 |
0.0009 |
0.0020 |
2.22 |
|
b. Analytical statistics |
|
Test |
t |
d.f. |
Two-sided p |
|
Raw data |
|
|
|
|
tpooled
variance |
2.114 |
18 |
0.049 |
|
tseparate
variance |
2.114 |
14.8 |
0.052 |
|
Exact Wilcoxon-Mann-Whitney |
|
|
0.072 |
|
Exact permutation on means
|
|
|
0.049 |
|
log10-
transformed data |
|
|
|
|
tpooled
variance |
2.123 |
18 |
0.048 |
|
tseparate
variance |
2.123 |
15.8 |
0.050 |
|
Exact Wilcoxon-Mann-Whitney |
|
|
0.072 |
|
Exact permutation on means
|
|
|
0.048 |
|
n1,n2
= Group sizes; , ,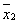 =
means for groups xl and x2 (normal ,
chronic obstructive =
means for groups xl and x2 (normal ,
chronic obstructive
airway disease);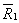 , , =
mean ranks for groups xl and x2 ; SE1,
SE2 = standard errors for =
mean ranks for groups xl and x2 ; SE1,
SE2 = standard errors for
xl and x2 ; 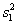 , , =
sample variances for xl and x2. =
sample variances for xl and x2.
|
|
表3.
Global outcome and multiple pair-wise contras by dose, from
RM-ANOVA (see fig.1) |
|
Dose, μg |
p |
p’ |
|
6.25 |
0.041 |
0.164 |
|
12.5 |
0.469 |
0.938 |
|
25 |
0.027 |
0.135 |
|
50 |
0.0012 |
0.0072 |
|
100 |
0.064 |
0.192 |
|
200 |
0.728 |
0.938 |
|
For parallelism of fall in blood pressure
according to dose of placebo and antagonist:Pg-g=
0.0156(Greenhouse-Geisser cor- rection). Thus the profiles
placebo and antagonist over increas- ing dose can be
regarded as different. p= Raw two-sided p values for
contrast of placebo versus antago-nist; p’= raw p values
adjusted for 6 comparisons by Ryan-Holm step-down Bonferroni
procedure. |
|
 |
|
圖1.
兩處理對於血壓降之影響顯著性比較 |
|
|
|
附錄1:常用的統計符號 |
|
N |
樣本或母群數值 |
|
 |
樣本或母群平均值 |
|
SE |
平均值標準差 |
|
s |
樣本或母群標準偏差 |
|
s2 |
樣本變異數 |
|
T |
學生氏t檢定 |
|
F |
F檢定 |
|
r |
皮爾孫之相關係數 |
|
x2 |
卡方分配 |
|
p |
第Ⅰ,Ⅱ型誤差之或然率 |
|
p’ |
p之調整值 |
|
α |
第Ⅰ型錯誤之機率 |
|
β |
第Ⅱ型錯誤之機率 |
|