|
此篇文章出自:Biochemia
Medica 2009,19(2):127-136。為此期刊「Lessons
in biostatistics」之系列文章。題目為「Describing
and interpreting methodological and statistical techniques in
meta-analyses」。
「Meta-analysis」已成為一個普遍使用的統計技術,自各個研究文獻進行解釋,由相近的報導、技術或處理,將其數據或結果整合在一起加以分析。對於一些大量且不一致的數據,或是不相同(inconclusive)的文獻,或是原始的數據,加以了解其真實的意義。使用Meta-analysis最大的挑戰是其資料來自不同的研究設計,各研究有不同的研究標準,尤其在醫學上不同的解釋方法。使用Meta-analysis進行分析,必須了解此統計方法、意義、目的與最終的影響。使用此方法係自文獻資料中解釋結果,必須了解其優點與限制條件。
一、引論
Meta-analysis是一個已使用30年的統計技術,用以整合知識。在醫學、工業與基礎科學的領域,嘗試自各種資訊中加以歸納。在過去的許多研究論文,研究者經常使用的文獻是這些文獻的結論合乎他們自己的研究。新的數據與新的敘述都是作者在現有的期刊加以表現用以更新其研究領域。這些方法也可稱為「部份Meta-analysis」。因為有過去的文獻歸納知識,增加他們自己對於新數據、新的發現,而藉以更新新的知識。但是這些新的數據研究並未以確實的統計方法整合過去的數據。只是採用過去的數據以判斷比對現有的研究。
Meta-analysis則是將有的知識背景(base)加以組合。不管是已出版的論文或是原始未處理的數據,以統計技術合成所有的知識。所得到的結論是基於這些資料在過去的貢獻。
Glass對Meta-analysis的定義如下:「Mate-analysis是對分析對象進行分析,以統計技術對於各個體所得到的大量資料進行分析。其目的就是整合所有的發現」。在許多學門,統計分析的結果可能是平均值影響,反應比例,風險比例,相關性等。以下的內容只是Meta-analysis的簡介。更複雜的統計分析,例如Bayesian與非參數檢定則不加以介紹。
二、系統性的評論
醫學的研究都是一個問題開始,例如「Statins是否能夠減低癌症風險?」「Plasma
vitamin是否為Vitamin
C所吸收的生物性指標?」。這些問題可以自研究論文或研究報告,加以分析,以得到一個肯定性結論(definitive
conclusion)。這種方法稱為系統性評論(systematic
review)。這些系統性評論其研究步驟包括:1.研究的問題2.對原始之論文進行系統性搜集3.選用適合的論文4.對於選取論文進行分析。在醫學上常使用的文獻庫有:
1.
MEDLINE(Medical
Library of Medicine database)
2.
EMBASE(medical
and pharmacologic database by Elsevier publicly)
3.
CINAHC(cumulative
index to nursing and allied health literatures)
4.
CANCERLIT(cancer
literature research data base)
對於文獻的資料不論是定量或是定性,進行系統性的評論與數據解釋,這些都是Meta-analysis。統計分析的結果。包括常見的mean
effects, response rates, odds ratios, correlation等。
三、樣本大小的影響
樣本數目對於統計差異性的影響,由最簡單的兩個處理比較開始。例如A是新的處理,用以降低血壓值。B是對照值,樣本影響大小(Sample
effect size, ES)
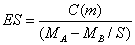
MA為A處理所血壓降低的平均值,MB為B處理對降低血壓的平均值。S為兩組數據的綜合標準偏差。
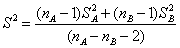
SA與SB為樣本A與B的標準偏差(standard
deviations)。nA與nB與A與B處理的樣本大小。C(m)稱為校正子。用以評估因為樣本數目太小時對真正影響值ES的偏估量(bias
estimating)。其計算公式:
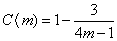
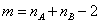
樣本數目不斷增加後,C(m)值收斂而趨近1.0。ES的變異量其計算公式如下:
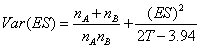
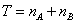 ,3.94為校正常數。 ,3.94為校正常數。
更複雜的例子如下:有更多的研究數據,K>6。原來的對照組為A,但是在meta-analysis,A組之數據形式(form)不見得與其他數據資料相同。例如其他一個處理可能是配合運動,另一個處理可能是添加維他命C。對對照組而言,某一處理之對照組可能給予安慰藥,而另一處理之對照組可能是運動。而進行Meta-analysis,有興趣的問題在於其他方法是否比對照組A,更能降低血壓。
在K處理中,其影響因子ES,可標誌為ES1,ES2…ESk,平均影響大小(mean
effect size)為ES(mean)。

Wi代表自
1,2,…,k,的加權係數。
對Mata-analysis而言,每組數據的加權比重不應相同。例如一組數據有500個量測對象,其加權比重應該高於一組數據有80個量測對象。加權係數也可依據量測之時間點而不同。以存活分析而言,10年的調查數據,其加權比重應該高於5年的調查數據。加權係數的評估計算其實十分複雜。最常用的方法,是將加權係數取為ES變異數的倒數。
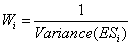
較大型的研究,有更多的精確值,其變異數較小,因此其加權值則是更大。
另一種加權係的選擇方法是其對研究的貢獻比例。例如Nt為參與研究樣本總數,共有K個研究,
 ,Wi的計算公式為: ,Wi的計算公式為:
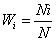
此種方法的基本條件為自i=1至K,每組數據其變異數不能相差太大。
每一個i處理,其變異假設相近,此稱為meta-analysis的固定影響。如果每個處理的變異都加以考慮,此稱為任意影響(random
effects)
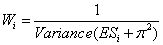
π2為各研究之變異。π2之計算十分複雜,許多統計計算軟體已經有此程式提供計算。
以最簡單的A、B處理為例證,A為新的處理,B為對照組。來自原有K個研究結果。
假設δ為所有綜合ES(mean)的族群值,虛無假設為新處理A與原來K組研究之B處理,兩者無差異,H0:δ
=0,其對立假設Ha: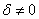 。以95%信賴區間計算族群平均值的信賴區間。 。以95%信賴區間計算族群平均值的信賴區間。
[ES(mean)-1.96π , ES(mean)+1.96π]
如果此信賴區間包括零,即代表A處理是無差異。
以下以一個例證進行說明,處理A與處理B有9個研究報告,其ES之比較為:0.574,
-0.642, 0.363, -0.840, -0.783, 0.833, 0.842, 0.803, -0.345。這些數據顯示,五個為正,代表A較好。四個為負,代表B較佳。計算結果對固定影響ES(mean)
= 0.86,t=0.109。對任意影響π=0.243。固定影響之95%信賴區間(-0.127,
0.299),任意影響信賴區間(-0.387,
0.563)。兩者都包含零。因此在9個研究顯示A處理並未顯著優於B處理。任意影響之信賴區間其範圍高於固定影響,這是來自變異數之影響。
四、異質性的討論
Meta-analysis另一個判別是處理之間是否顯著相異,此稱為異質性分析。使用之統計量稱為Q,用以判別異質性的程度。如果Q值接近零,代表無異質性。Q為k-1自由度的平方分佈。Q值經過計算與卡方分配的臨界值(critical
valve)比較。虛無假設H0,
Q=0代表所有數據群無顯著差異。對立假設HA:Q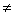 0,代表有顯著的差異性。例如在9個研究中,其卡方分配,df=8。α=0.05之臨界值為16.919,Q值為計算值為38.898,代表虛無假設被拋棄。此結果並不是代表A處理無顯著差異,而是警告研究人員關於資料來源的異質性。這些異質性可能來自臨床試驗的不同,例如選擇的病人對象,疾病嚴重性的底線等。另一方面,研究方法也可能有所不同。 0,代表有顯著的差異性。例如在9個研究中,其卡方分配,df=8。α=0.05之臨界值為16.919,Q值為計算值為38.898,代表虛無假設被拋棄。此結果並不是代表A處理無顯著差異,而是警告研究人員關於資料來源的異質性。這些異質性可能來自臨床試驗的不同,例如選擇的病人對象,疾病嚴重性的底線等。另一方面,研究方法也可能有所不同。
異質性的比例,可以以I2此統計參數加以表示。I2由ESi值加以計算。I2之解釋為π2值引起之變異比例。I2=79.4%,代表79.4%的變異或是異質性是來自π2值,或是說來自研究之間的變異值。
五、Publication
bias
將ES對樣本大小製圖,或是以ES對標準差(SE)製圖,稱為Funnel
plots,用以評估Meta-analysis的有效性。
如果Meat-analysis無固定偏差,Funnel
plots為左右對稱之圖形。如有有固定偏差存在,funnel
plots為不對稱或是呈現Skewness
Funnel plots的對稱性可以以迴歸分析檢定。以ES對估計值精密性進行迴歸,精密度為標準差的倒數。線性公式如下:
ES = a + b*精密性。
由於精密性與樣本的大小相關,小樣本其精密性在水平軸將接近零。如果截距為0,則無法拒絕虛無假設。代表上述程式之a值與零無顯著差異。 |