|
執行迴歸分析研究之後,研究人員往往討論如下的問題,使用的模式與這些量測數據有多大的符合性?最被使用的判別標準即是決定係數(Coefficient
of determination),R2。在學術研究上最通俗的觀念是R2愈接近1.0愈好。
R2是什麼,在統計教科書的定義如下:
R2= SSReg/SSTotal
(1)
SSReg稱為迴歸模式的變異量,SSReg計算公式如下:
SSReg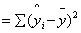
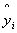 為迴歸模式在yi點的預測值, 為迴歸模式在yi點的預測值,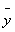 為所有yi值的平均值。 為所有yi值的平均值。
SSTotal稱為yi值之變異量,SSTotal計算公式如下
SSTotal 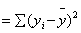 (2) (2)
R2的定義代表迴歸模式之變異值與所有yi變異量之比例,R2愈大,代表此迴歸模式能夠解釋全體yi變異量的比例愈大。因此R2愈接近1.0,代表此模式愈有解釋能力。
使用R2值作為判別標準,至少有兩大問題:
1. R2值要多大才是有價值?
關於社會科學研究,R2值為0.5或0.6則是常見,R2值大於0.7則很少見。生物或農業研究,R2大於0.9也是不多。但是在儀器效正公式,R2值通常為0.999。因此R2值要多大才有判別價值?
2. R2值愈大,不見得模式是正確。
許多線性迴歸式,R2值高達0.99,但是其殘差圖檢定顯示多項式才是正確的校正公式。
以R2值為判別的標準,最大的問題是R2值可以人為加以調整改變,由R2值計算公式可以推導成如下公式:(R.
H. Myer,Classical and Modern Regression with Application, PWS and Kent
Publisher, 1986)。
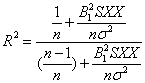 (3)
(3)
以W
= 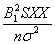 (4) (4)
公式(3)可以改為
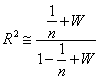 (5)
(5)
因為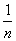 與W比較,可以忽略,公式(5)為 與W比較,可以忽略,公式(5)為
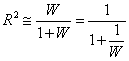 (6)
(6)
公式(6)代表W愈大,R2相對愈大。只要人為增加W,R2值就變大。影響W值的因子有三個。
1.
B:迴歸模式的斜率
2.
Sxx,Sxx的計算公式為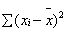 。因此數據在X軸愈分散,Sxx愈大,R2就愈大。 。因此數據在X軸愈分散,Sxx愈大,R2就愈大。
3.
n,n為數據數目,n愈小,W愈大,R2愈大。
由上述討論可知如何提高R2值,這些技巧(Tricks)在生物感測器最常見。
1.
提高Sxx值,將迴歸分析之數據點其分布範圍擴大,例如X之範圍原來為20ppm~35ppm,只要增加一個數據點Xi
= 100ppm,其R2值即暴增。
實例一:以一個生物反應器之研究論文為例,X值為MBA
Titer,Y值為Reference
Vessel Titer。圖1代表X數據分佈為1600以內,其迴歸公式:
Y1 = 53.113+1.1127X, R2= 0.853。
增加一組數據(X
= 2225),分佈如圖2,其迴歸式:
Y2 = 16.4975 +1.2011X, R2= 0.912。
再增加一組數據(X
= 3750),分佈如圖3,其迴歸公式:
Y3 = 73.4804 +1.0830X, R2= 0.981。
由此實例可知,增大X之分佈,即增大Sxx值,對R2之影響有多大。
2.
減少n值
常用的方法是以各組平均值代替所有數據,例如Xi為10,20,30,40,50ppm,在每個Xi值有3個量測值(yi1,
yi2, yi3),共有15組數據。如果以Xi條件之3個量測值加以平均值為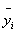 ,則只有5組數據。 ,則只有5組數據。
以15組數據與5組數據進行迴歸分析,以線性公式為例,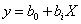 。兩種數據所得之bo與b1值完全相同,但是R2值大有所不同。5組數據迴歸所得R2值遠大於15組數據之R2值。 。兩種數據所得之bo與b1值完全相同,但是R2值大有所不同。5組數據迴歸所得R2值遠大於15組數據之R2值。
實例二:一篇電化學伏安法量測農藥殘留濃度之論文,其原始數據分佈如圖4,其迴歸公式為:
Y1 = -0.2613+0.8560X, R2= 0.923
以Yi之平均值對Xi重新製圖,數據分佈如圖5,其迴歸公式為:
Y2 = -0.2644+0.8552X, R2= 0.983
由此可知以原始數據或以平均值進行迴歸分析,對R2值影響有多麼顯著。
R2是否有意義的判別標準?看看許多學術論文其數據呈現方式即可看出端倪。
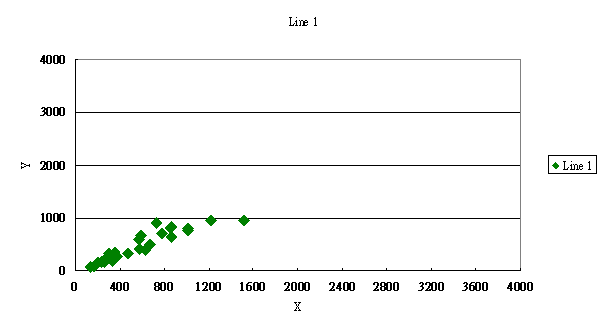
圖1.
X數據分佈範圍為0- 1600之間
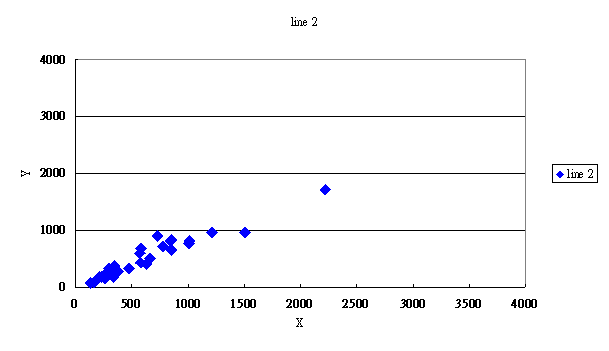
圖2.
X數據分佈範圍為0- 2225之間
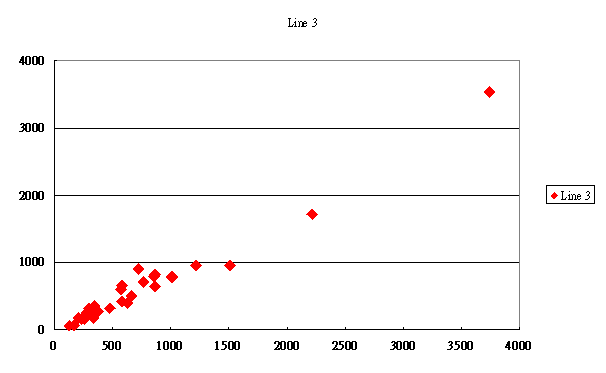
圖3.
X數據分佈範圍為0- 3750之間
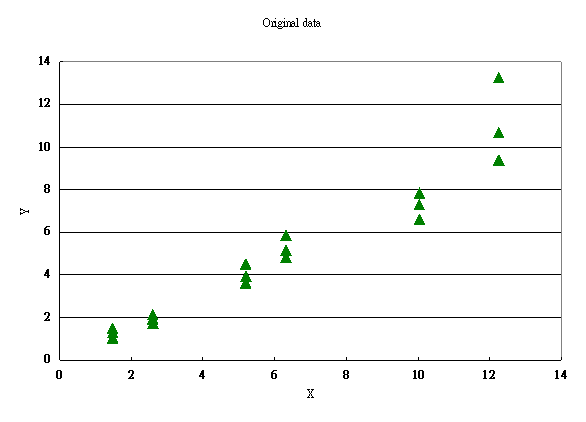
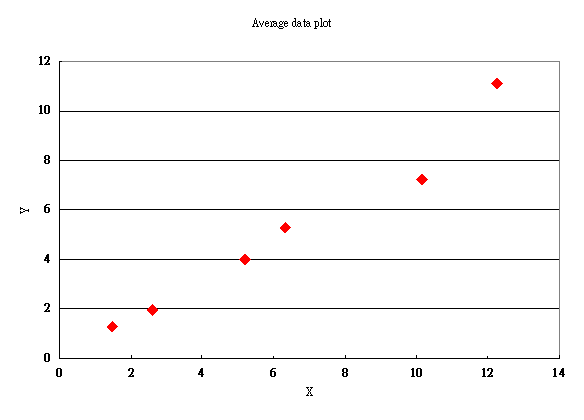
圖5.
電化學伏安法量測農藥殘留濃度之研究其平均值數據分佈
|