P值要多小？

中興大學 生物系統工程研究室 陳加忠

資料來源：Weimo Zhu，P<0.05，<0.01，……..<0.000001，or<0.0000001，

Journal of Sport and Health Science 5(2016)77-79

在科技期刊上似乎進行著最小P值的競賽，代表有更多顯著性的發現。在網路上搜尋〝P<0.00000001〞，就可發現有許多論文報導，其P值是如此之小，P值真的能夠如此之小？目前的統計軟體都有P值得報導，此導致了科學研究的沼澤或是死巷。

為了瞭解為何只憑藉著P值是一個錯誤方法，首先討論在沒有電腦運算之前，P值，假設檢定(hypothesis testing，HT)與統計假設檢定(statistical hypothesis testing，SHT)。現在P值與假設檢定都是在統計假設檢定的保護傘下使用，但是根源不同。P值與其在科學研究之利用是來自於1925年英國統計學家Sir Ronald Aylmer Fisher。在Fisher的查詢系統中，一個檢定量的統計量以機率表示，稱為P值。在虛無假設下，試驗統計使用機率分配，P值只是用以輔助。在收集數據之後，評估此觀察統計量是一個簡單任意事件或是確實屬於一種符合科學家其科學假設下得一個單一事件。而且0.05或0.01並不是唯一用以進行判斷(決策，decision)之唯一標準。因此Fisher的P值查詢系統是一種後天性(posteriori)決策系統。代表〝有變化性，更適合特別指定之研究計畫，用以進行簡單的歸納與檢定力分析，沒有對立假設〞。

相反的，假設檢定(HT)是1933年來自波蘭數學家，Jerzt Neyman與美國統計學家Egon Pearson。為了應用於重複性試驗而且希望能夠改善Fisher的方法。Neyman與Pearson認為除非可以提出一個替代(alternative)假設，否則虛無假設不應該加以考慮。

與Fisher系統不同，Neyman-Person系統強調了要使得第一型錯誤為小化(Type Ⅰerror to minimize )，檢定的標準與相應的系統區域必須事先預定。因此Neyman-Pearson系統屬於先天(Priori)決策系統。此系統特別適用重複取樣的研究。

目前主要的統計假設檢定是推導於Neyman-Pearson系統。P值由現代的統計軟體加以計算。因此研究人員開始將兩系統加以混合，結果導致統計假設檢成為培育偽科學(pseudoscience)的一種工具。

對於電腦時代之前的統計假設檢定作法加以複習，就瞭解上述觀點，一個典型的統計假設檢被應用於決策系統，必須包括以下步驟：

1.決定虛無假設(H₀)與對立假設(H₁)

H₀：假設為真

H₁：通常為研究這的假設

2.設定第一型錯誤的臨界值(α)，代表H₀為真不應該被拒絕，結果被拒絕錯誤機率。實際上，α值往往被P值取代，由α值形成一個特別區域，用以區隔拒絕或不拒絕的臨界範圍。

3.選擇一種統計試驗與設定決策規律。此即用以揚棄虛無假設。此設定包括第一型錯誤機率，使用一尾檢定或二尾檢定，樣本數目等。

4.以選用的檢定方法計算統計量。

5.由上述(3)以進行決策。

統計假設檢定類似美國法院審判制度，人被假設無罪，直到證明有罪。

H₀：被告是無罪。

H₁：被告是有罪。

如果H₀被拒絕而事實上H₀是事實，此稱為第一型錯誤。代表一個無辜者被判有罪，而實際上他是無罪。因此第一型錯誤必須比第二型錯誤更加嚴格管理。在使用電腦軟體計算之前，P值或第一型錯誤值必須預先決定。通常只有兩種選擇，例如對於人體工學研究，P=0.05，對於藥學研究，P=0.01。因此統計假設檢定屬於先天系統。評估的機率標準或是信賴區間，必須預先建立，再來計算統計量，然後進行決策。

以一個研究案例說明上述步驟。一個研究人員研究男女生其體脂含量比例是否不同，而假設女生有較高的體脂肪比例。試驗人數共10人(5男，5女)。

統計假設檢之步驟如下：

1.設定H₀與H₁

H₀：女生肢體脂比例=男生之體脂比例

H₁：女生肢體脂比例≠男生之體脂比例

2.設定第一型錯誤

α=0.05

3.選擇檢定方法與建立判別規定

使用獨立t檢定，α=0.05，雙尾試驗，自由度df=8，t檢定量由t表查為2.3060。

如果-2.306< t值<2.306，H₀不能拒絕

如果t≦-2.306或是t≧2.306，拒絕H₀

4.計算t值

女生：平均值=23.958，標準差8.33

男生：平均值=15.942，標準差10.646

t：(23.958-15.942)/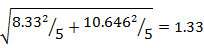

5.進行決策

因為t值不小於-2.306或不大於2.306，H₀不能拒絕。使用電腦軟體計算時，提供了精確的P值。例如上述試驗之P值為0.221，因為H₀無法拒絕，男生與女生在體脂肪比例並無差別。

在普遍使用電腦軟體之後，研究人員開始在其論文報導P值，而對相關重要資訊不再說明，結果導致現在在科學期刊看到的P值最小值競賽。

假如不需要其他統計資訊，P值可以得到相同結論，那就沒有問題？然而P值有兩個問題。

1.改變了統計假設檢定決策中事先決定統計量之概念。原來在進行決策之前，必須先決定判定標準。

    2.更嚴重之問題，P值受到樣本數目嚴重影響，使得決策標準的不一致。

已上ㄧ個例子而言，要使P值小於0.05或拒絕H₀並不是困難，只要具有足夠的檢定力，就可以判定H₀為偽。

有4個因子影響了檢定力：

a.α值

b.單尾或雙尾檢定

c.結果大小(Effect size，ES)

d.樣本大小

因為α值與單尾或雙尾檢定，通常已是固定，ES與樣本大小實際上影響統計檢定力，ES可由Cohen´s d index加以計算

ES(cohen´s d)=

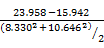                      = = 0.839

依據Cohen´s ES標準(> 0.8，大；<0.8至>0.2，中等；≦0.2，小)。此例子中男生與女生之ES值為顯著大。那麼為何H₀未被拒絕，原因在於樣本數目，以ES=0.839，計算足夠的樣本數目，樣本數目為24。因此上述試驗男生與女生需要各再進行19次試驗。以上述數據重複使用4次

女生體脂比例：平均值 = 23.958，標準差 = 7.644

男生體脂比例：平均值=15.942，標準差=9.75

 t=2.89， P=0.006

上例說明，平均值不變，標準差變小，t值變大，P值小於0.05，結論為顯著差異。

由此可知，樣本數目太小，無法得到真結論，而且在樣本數目很大時，只有一點點差異，或低相關性都可能成為顯著差異。這種不一致結果，使得在進行統計檢定時P值反而無用。

由上述程序可知，只要先決定ES，要得到P<0.005之樣本數目即可計算。因為Cohen´s d檢定可用以評估小，中，大之比例。因此不能只用P值進行判別。

對P值與統計假設檢之批評，至少已有80年之歷史。P值被批評濫用，是因為被做為唯一的判別條件。除了使用ES，其他可用方法包括探索數據分析(exploratory data analysis)，信賴區間(confider interval)，mete - analysis與Bayesian應用。

現在有許多期刊，要求報導P值，對於統計檢定建議如下：

1.證明決定α值，例如〝We used an α level of 0.05 for all statistical tests〞。

2.對於相關係數，使用絕對標準。

  0~0.19，無相關

  0.2~0.39，低相關

 0.4~0.59，中度相關(moderate correlation)

 0.6~0.79，相關性高(moderately high)

 ≧0.8，高度相關

3.對於回歸分析，要報導其他統計量。

4.對其他歸納統計，df，ES等統計量要報導。

5.有兩個方法報導P值

a.報導P值是基於α值，例如α〝P>0.05或P值<0.05〞

b.報導確定之P值，如果P值小於0.001，報導如下：P<0.001

6.以〝statistically not significant〞表達，而不使用〝not significant〞。