|
此篇論文來自一個特別的醫學期刊,Nepal
journal of Epidemiology創刊號第一篇文章2010,1(1):4-10,篇名為「Relevance
of Sample Size Determination in Medical Research」。
一、背景
在醫學研究,樣本的數目大小十分重要,才能確保可靠的結論。如果研究已經過良好的設計,又有足夠的樣本數目,其標準差將是降低,其精確性與檢定力更好。在研究中的統計程序則是有效。
歸納統計法包含兩部份,母群參數的統計值與假設檢定。根據醫學研究的型式,上述兩個方法都可應用。參數估計主要應用於流行(Prevalence)敘述(descriptive)研究。假設檢定主要應用於世代(Cohot),病例對照(Case
Control),與臨床試驗(Clinical
trials)。使用參數估計方法,可得到母群特性最佳估計值,例如流行程度(Prevalence)發生率(incidence),mean
,standard,deviation等。使用統計檢定,變量之間的關係能夠加以評估驗證。
醫學研究數據在進行統計分析之前,必須先進行兩項統計假定。第一個檢定是常態分佈檢定。由常態分佈檢定結果,再決定使用參數分析或非參數分析。第二個檢定是樣本的數目。如果樣本數目不適當,處理之間實質上有差異,統計結果應是不顯著。樣本數目太小,導致不正確的結果,浪費研究者的時間與資源。樣本太大,損失了研究經費,浪費研究人力。
二、樣本數目的影響因子
1.
研究的檢定力
檢定力(Power)代表探查真正差異的機率。例如在病害已出現能夠得到正結果的可能性。一個好的研究,其檢定力至少要大於80%。增加試驗的樣本數目,或是試驗組與對照組的差異愈大,檢定力就增加。然而樣本數據的標準差愈大,顯著水準(significance
level)增大,試驗之檢定力則減低。
2.
顯著水準
顯著水準代表如果此事件(虛無假設)是真實,在統計檢定時被拒絕的機率。因此在假設檢定進行之前,在計算樣本數目之前,都必須先固定此數值。
在進行假設檢定與估計樣本數目之前,必須先決定信賴水準。通常信賴水準數值為0.05或0.01。信賴水準與檢定力之代表數目如下表一:
-------------------------------------------------------------------------------------------
信賴水準
檢定力
(Significance level) (Power)
---------------------------------------------------------------------------------------------
5% 1% 0.1% 80% 85% 90% 95%
----------------------------------------------------------------------------------------------
1.96 2.58 3.29 0.84 1.04
1.29 1.64
-----------------------------------------------------------------------------------------------
3. 事件率(Event
rate)
對研究對象(族群)而言,如果事件比例是預先且固定,檢定力則較高。如果試驗所得事件比例低於期望值,樣本數目要重新估計。
4. 順從性(Compliance)的影響
Compliance是直接影響樣本數目的重要因子。其調整公式如下。
每一研究群的樣本數目原來為n,調整公式:
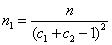 (1)
(1)
c1與c2為每一族群的平均順從性比例。
三、敘述性研究之樣本數目
1.研究參數為平均值
E代表量測誤差的臨界值,95%的信賴區間,其計算公式是1.96乘以標準差。
 ,因此 ,因此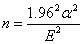 (2)
(2)
如果為99%的信賴區間:
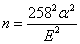 (3) (3)
例題如下:心跳數目為70次/min,標準差為8次/min,在α=1%,可允許之誤差為1次/min,需要的樣本數目:
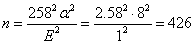
2.
研究參數為比例值
P為母群之比例值,Q=1-P
95%信賴程度,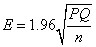 , ,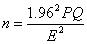 (4)
(4)
例題:未處理HooKworm流行率為30%,在5%之信賴度,允許誤差為10%,需要之樣本數:
E=30% X
10% =30%

四、分析性研究
分析性的研究設計是用以檢查病原(etiology)與原因(Cause)之關聯性。此種統計分析稱為分析性研究(Observational
studies)與實驗性研究-臨床試驗(Experimetal
studies-Clinical trials)
1. 對病例-控制(Case-control)研究-雙頂(binary
exposure)計算樣本數
研究病例群樣本的數目為n,r為對照群(Controls)對病例群(Cases)之比例
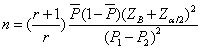 (5)
(5)
(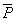 )
與( )
與(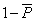 ):差異數的量測(類似標準差) ):差異數的量測(類似標準差)
Zβ:預定的檢定力,如表一。
Zα/2:預定的統計顯著水準,例如1.96
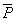 =(P1+P2)/2 =(P1+P2)/2
Pcontrol-exp為控制群之比例值。
Pcase-exp為對照群(Case
group)之期待比例值,其計算公式:
 (6)
(6)
例題:在一項觀察研究中,希望觀察之勝算比(Odds
Ratio (OR))為2.0或2.0以上,ZB
= 0.84。對0.05信賴水準,Zα/2
= 1.96。
R為病例群與對照值之數目比例。此研究中r
= 1.0,對照組之比例值為20%。
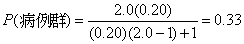
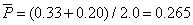 ,代入公式
(5) ,代入公式
(5)
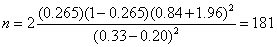
因此樣本所有數量為362。(病例181,對照181)。
2.
病例與對照為continuous exposure,計算其樣本數目
n計算公式如下:
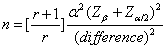 (6)
(6)
n:病例群之樣本數
r:控制組對病例組之比例
α:結果變數(outcome
variable)之標準差
difference:平均值差異性之有效值
例題:80%的檢定力,Zβ
= 0.84,Zα/2
= 1.96,r
= 1.0,σ
= 10.0
Difference = 5.0,代入公式
(6)
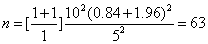
需求樣本數量為126(case:63,control:63)
3.
獨立世代(Cohot)研究之樣本大小
A需要預先決定之知識或條件
1. 檢定力(Power)
2. α值
3. P0:控制組之事件或然率
4. P:病例組之事件或然率
5. RR:對病例組與控制組事件之相對風險(risk)
RR=P1/P0
6. m:每一試驗對象的控制數據
B、注意事項:
1. 經常使用的Power值為80%,85%,與90%
2. α值通常為0.05
3. P0可由現有觀察流行病中得到比例值
C、n之計算公式

 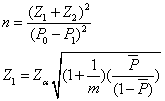 (7,8) (7,8)
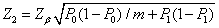 (9)
(9)
 (10)
(10)
 (11)
(11)
β = 1 – Power
Nc:為continuous
corrected sample size
五、實驗性研究
1.
比例值差異性之簡易公式
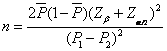 (12)
(12)
n:每一試驗群的樣本數目
(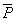 )( )(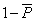 ):差異值之量測變異數 ):差異值之量測變異數
P1-P2:有效的差異值(比例值的不同)
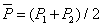
2.
平均值差異性之簡易公式
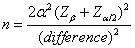 (13)
(13)
3.
每一試驗群的樣本數目不同之計算公式
(1). λ:代表安慰劑使用之樣本數
(2).
每一個情況(Case)其數目不大於4-5個
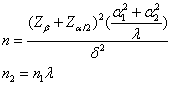 (14)
(14)
4 .
一定比例之樣本數目
條件:每一樣本的變異值相等
樣本之比例值為:
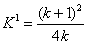 (15)
(15)
應用例子:二個相同樣本群其總數為26,希望樣本比例為2
: 1
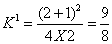
總數目:26*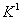 =29.25,樣本數目為30. =29.25,樣本數目為30.
因此第一群數據為20,第二群數目為10.
5.
調查的事件數目(number of events)特別重要
此公式針對世代(Cohort)試驗中,exposed與非exposed對象
其相對風險R,π1為未暴露族群之流行率
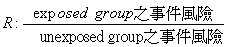 (16)
(16)
 (17)
(17)
n1: unexposed group之事件數目
n2: Rn1 = exposed group之事件數目
N = n1/π
N代表每一組群中需要的樣本數目
6.
重點為受測對象,其共變數與數目
a.每一研究主題至少10個樣本,使用LOGISTIC迴歸分析,主要用以穩定樣本(Stability)非用以檢定力(Power)。
b.
進行主成份分析(PCA),樣本數目N,N
> 10m+50或n
> ㎡+
50 (18)
m為每一試驗對象之控制組樣本數目。
7.
進行單一t檢定或成對t檢定
a. 目的是假設檢定,H0 :μ=k,
b.
雙尾檢定,樣本數目
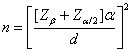 (19)
(19)
8. Lehr‘s公式
用於成對或非成對t檢定,或是卡方檢定。
a. 檢定力為0.8(80%),α
= 0.05
b. 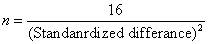 (20) (20)
c.
非成對檢定,每一族群小於30
Standanrdized differance =
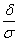 (21) (21)
每一數據群,樣本數目為N/2
d.
假設兩樣本群之變異相等。
五、聚集任意試驗(Cluster
randomised trial)
研究工作面臨經費、人力、時間等限制,而且疾病集中於特定區域,可使用聚集任意試驗以估計樣本數目。
常用的符號如下:
k:聚集數目,例如村莊、社區、學校、班級等
m:聚集大小(至少5人)
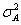 :聚集之間變異數(Varicnce
among the clusters) :聚集之間變異數(Varicnce
among the clusters)
 :聚集之內變異數(Within
cluster variability) :聚集之內變異數(Within
cluster variability)
ρ:ICC(intracluster
correlation coefficient)
i:
intervention group(i
= 1,treatment;i
= 2,control)
1. Design effect
N = 1 +(聚集數目(Number
per Cluster) -1)x
ICC (22)
此公式假設每一聚集的數目相同
2. Continuous outcome
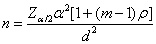 (23)
(23)
σ:結果的標準偏差
ρ=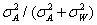
聚集需求數目k
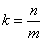 (24)
(24)
3.
兩項式結果(binary outcome)
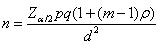 (25)
(25)
ρ與k之計算與上式(24)相同
4.
假設檢定(Testing of Hypothesis, RCT)
用以比較平均值,每一聚集的數目相同
虛無檢定為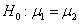
 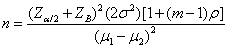 (26)
(26)
 :intervention
group 平均值 :intervention
group 平均值
 :Control
group平均值 :Control
group平均值
如果聚集群之數目不同,以 或mmax代替m 或mmax代替m
六、經驗與建議
1.
如果與對照組比較,臨床處理的影響並不顯著,試驗的檢定力不高,P值較低於預期值,樣本數目需要增加。
2.
如果量測值變化太大,使用平均值或增加重覆數次。
3.
以專業決定可接受的信賴程度(α)與可接受檢定力(1-β)。
4.
自類似的族群先行估計事件率。
5.
以初步試驗,配合統計技術決定樣本數目、試驗檢定力,與順從性(compliance)等。
6.
在一個族群內分成多重次族群,每一次族群之樣本數目應該增加至適當數目。
7.
對小負面試驗(Small negative trials)可使用meta-analysis。
8.
如果需要與其他單位配合以進行大樣本數目的試驗,建議使用
Multi-centre trials。 |