|
資料來源:
Biochemia Media 2013; 23(2):143-149.
獨立性的卡方檢定又稱為Pearson卡方檢定,或是簡稱卡方檢定。在醫學研究上,卡方檢定可以用以檢定類別型數據,因此為一種有用的統計技術。卡方檢定不僅可提供任何觀察值是否顯著差異,也可得到哪項類別是歸因於此顯著差異。其檢定結果以陣列方式呈現其結果。
每一項統計檢定都有其基本假設,卡方檢定用於顯著性檢定,也有其基本假設。卡方檢定是一種非參數統計技術,在以下情況下加以採用:
1.
所有變數的量測值為類別型(nominal)或順序(ordinal)型
2.
每一研究群的標本數目不相同,一些特殊之卡方檢定其母群數據數目需要相等或是類似相等。
3.
原始數據之量測有其間隔或是比例程度,但是違反了下述的參數檢定:
a.
數據分佈為嚴重的偏斜(skew)或是峰態(kurtotic)。
b.
數據的變異量非常數。
c.
因為一些特殊原因,連續性之數據被歸類成為小族群。
一、卡方檢定之假設
非參數檢定其最基本假設為數據為隨機取樣。但是在歸納檢定中,數據也有來自便利抽樣(convinience
sample)。因此對每一試驗條件,至少要有多個重覆。卡方檢定之相關假設條件為:
1.
每一檢定格子(cell)內的數據應該設為頻率或計數數目,而不是百分比或是經過轉換之數據。
2.
每一變數之類別或水準(Level)相互排除。一個變數在一個特定水準只歸於一類。
3.
每一研究對象只能歸於某一特定格子,例如一個樣本在不同的時間進行測試,三個不同時間內得到之數據就無法採用卡方檢定。
4.
研究族群必須相互獨立。例如樣本為成對(母女),則不可使用卡方檢定,而是使用其他統計技術。
5.
通常以兩個變數加以分類。數據可為類別層次。數據也可能是順序數據。間隔或比例數據加以區隔成類別數據也可使用。卡方分析格子的數據數目未有限制,但是超過20格子則很難進行檢定與解釋。
6.
至少有80%以上的格子,其數據至少大於5。樣本數目至少要為格子數目的五倍。
二、個案研究
一家公司的經理希望其員工都能維持健康,病假人數愈低愈好。肺炎在此地區十分普遍,導至員工病假。目前有疫苗可以對付球菌肺炎,經理相信疫苗可以使得員工免於患病。但是疫苗數量有限,只有半數之員工有機會接受疫苗。因此員工分成兩群:接種疫苗與未接種疫苗。公司對每一員工進行檢查,是否有感染肺炎。其調查數據如下:
第一群:接種疫苗(N1=92)
第二群:未接種疫苗(N2=93)
員工之檢查結果有三型:
1.感染球菌肺炎型之肺炎
2.感染其他型肺炎
3.無感染
此公司開始探討接種疫苗是否對於肺炎此病害有否效果。卡方檢定被採用以回答此問題。疫苗之預防結果如表一。
|
表一 疫苗接種之影響 |
|
結果 |
|
未接種 |
|
接種 |
|
球菌肺炎型肺炎 |
|
23 |
|
5 |
|
他型肺炎 |
|
8 |
|
10 |
|
健康 |
|
61 |
|
78 |
三、卡方值計算
卡方值之計算公式:
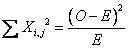
O為觀察次數,E為期望次數
χ2:每一格子之卡方數
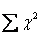 :所有格子卡方值之總值 :所有格子卡方值之總值
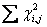 :代表自i格子至j格子的總和 :代表自i格子至j格子的總和
每行與每列之總值為邊際值
(marginal)。表一重新整理如表二。
|
表二 邊際值之計算 |
|
結果 |
|
未接種 |
|
接種 |
|
列(Row)邊際
值 |
|
球菌肺炎型肺炎 |
|
23 |
|
5 |
|
28 |
|
他型肺炎 |
|
8 |
|
10 |
|
18 |
|
健康 |
|
61 |
|
78 |
|
139 |
|
行(Column)邊際值 |
|
92 |
|
93 |
|
N=185 |
(二)卡方檢定的第二個步驟是計算每一格子之期望值。期望值代表無疫苗的影響時,每一格子之估計值,期望值的計算公式:
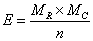
MR:行邊際值之格子
MC:列邊際值之格子
n:所有樣本數
(三)卡方檢定第三個步驟是計算χ2值。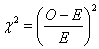 ,以表三代表每一格子之期望值與平均值。 ,以表三代表每一格子之期望值與平均值。
|
表三 邊際值之計算 |
|
|
|
未接種 |
|
接種 |
|
結果 |
|
期望值 |
|
卡方值 |
|
期望值 |
|
卡方值 |
|
肺炎球菌型肺炎 |
|
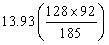
|
|

|
|
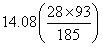
|
|
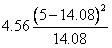
|
|
他型肺炎 |
|
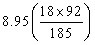
|
|
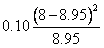
|
|
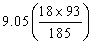
|
|
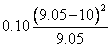
|
|
未感染 |
|
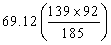
|
|
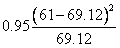
|
|
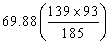
|
|
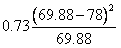
|
每一格子的卡方值完成計算之後,即可總計χ2統計量。
此個案之χ2值為12.36(5.82+0.1+0.95+4.56+0.1+0.73)
χ2表之自由度其計算公式:
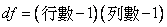
此個案中自由度為(2-1)(3-1)=2。查卡方表,卡方值12.35。自由度2時,其P值小於0.005,由精密計算之結果。P=0.0011:由於P值小於0.05,此研究之結果如下;拒絕H0,接受H1。
對於有接種疫苗與沒有接種疫苗之兩群,其肺炎之發生有顯著之不同。但是不同點在哪裡,需要進一步的解釋。
四、格子的χ2值之解釋
由表三可知,最大χ2值5.92發生於格子1。因為實際發生值為23。預期值為13.2。此格子之數據代表觀察結果顯著大於機率發生之數值。格子1代表非接種疫苗之員工其得到肺炎的人數遠大於預期值。第二大的χ2值為4.56,出現在格子2。代表觀察之數值(5)遠低於預期值(12.53)。有接種的員工其感染之人數遠低於預期人數。其它格子的卡方值都小於0.99。一個格子內之卡方值小於1.0,代表觀察得到的數值幾乎接近於預期值。因此對於非球菌之肺炎之患者獲健康無感染者,疫苗接種對其無顯著影響。
五、卡方與其相關檢定
類別型數據需要採用非參數統計,常用的方法有3種。第一種也是最常用的方法是卡方分析。第二種為Fisher’s
exact test。此方法比卡方分析更精確,但是只能使用於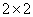 之表格。第三種方法稱為最大近似比例卡方檢定(maximum
likelihood ratio Chi-square test)。主要使用於樣本數太小的情況。 之表格。第三種方法稱為最大近似比例卡方檢定(maximum
likelihood ratio Chi-square test)。主要使用於樣本數太小的情況。
以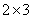 之表為例,共有6個格子,卡方檢定要求80%之格子其樣本數大於5。 之表為例,共有6個格子,卡方檢定要求80%之格子其樣本數大於5。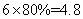 。由表一得知,每一格子(cell)內數據都大於5,因此可執行卡方檢定。 。由表一得知,每一格子(cell)內數據都大於5,因此可執行卡方檢定。
以表四說明小樣本數目之檢定。
|
表四 |
|
|
|
無疫苗接種 |
|
有接種 |
|
結果 |
|
數目 |
|
期望值 |
|
卡方值 |
|
數目 |
|
期望值 |
|
卡方值 |
|
球菌型肺炎 |
|
4 |
|
2.22 |
|
1.2 |
|
0 |
|
1.75 |
|
1.78 |
|
他型肺炎 |
|
2 |
|
1.67 |
|
0.07 |
|
1 |
|
1.33 |
|
0.08 |
|
無感染 |
|
14 |
|
16.11 |
|
0.28 |
|
15 |
|
12.89 |
|
0.35 |
雖然樣本數目39已超過基本要求(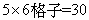 ),但是有4個格子其樣本數目十分小,以違背卡方分析之假設,因此必須使用最大近似比例卡方分析。 ),但是有4個格子其樣本數目十分小,以違背卡方分析之假設,因此必須使用最大近似比例卡方分析。
如果卡方檢定之基本假設已被違背,其檢定結果則不可靠。以卡方檢定面對適當或不適當使用之數據,其結果有三類,
1.
適當或不適當的檢定都得到相同結論
2.
適當檢定為顯著差異,不適當檢定得到無顯著差異,因此為第Ⅱ型錯誤。
3.
適當之檢定為無顯著差異,不適當檢定為有顯著差異,因此為第Ⅰ型錯誤。
六、卡方檢定之強度
以上述個案為例,P=0.0011,代表千分之1.1的機率代表有接種疫苗與無接種疫苗有千分之1.1之機會,兩者無差異。如果判別為差異,則可能得到第一型錯誤。因此進行卡方檢定也要測定此統計方法的強度(strength)。
統計顯著不見得代表臨床醫療的顯著。臨床顯著代表此處理有多大的改善。例如統計檢定之結果為顯著,但是肺炎感染之人數只有降低兩人,公司為了184名員工接種,比不接種處理只有減少兩名感染人數,在醫療成本上為不合乎經濟效益。
對於卡方檢定而言,最常使用的強度檢定稱為Cramer’s
V test。其計算公式如下:
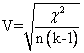
N為樣本數,k為行或列數目。
以此個案為例
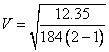 =0.259 =0.259
相關性為0.259,代表弱相關。
在上述個案中,有5個接種疫苗之員工感染球菌肺炎,大多數其他員工仍然健康,因此其相關性度不高,因此有顯著性。此強度檢定方法可用以解釋統計之結果。
七、結論
卡方檢定是一種高價值之工具,針對類別型數據進行檢定。在數據為隨機取樣,樣本數目又是足夠大,卡方檢定之能力十分適當。在數據之差異數不是常數,t檢定與ANOVA檢定無法適用,卡方分配可用以檢定。卡方值與Cramer’s
V值都容易計算。除了卡方分配,還有許多非參數檢定方法,都值得留意。 |