|
Statistical methods
for bioimpedance analysis
J Electr Bioimp,
vol. 5, pp. 14 –27, 2014
Christian
Tronstad1,3 and Are H. Pripp2
Department of
Clinical and Biomedical Engineering, Oslo University Hospital, Oslo,
Norway
Department of
Biostatistics, Epidemiology and Health Economics, Oslo University
Hospital, Oslo, Norway
E-mail any
correspondence to:
christian.tronstad@gmail.com
摘要
本文提供了有關生物阻抗測量分析其相關統計方法的基本概述,目的在於回答如下問題:如何開始進行實驗計劃?我需要進行幾次測量?如何處理大量的頻率掃描數據?我應該使用哪種統計檢定測試,以及如何驗證結果?從假設和研究設計開始,基於量測和統計分析進行推理的方法框架加以解釋。接下來是對相關量測和減少數據的簡短討論,然後概述了用於各組比較,因子分析,關聯性,迴歸和預測的統計方法,並在生物阻抗研究的背景下進行了解釋。給出了用於選擇統計方法的流程圖。
一.簡介
在進行測量時,如果我們要描述數據(敘述性統計)或要基於數據得出結論(推論統計),則需要統計。文獻中有大量的統計方法,選擇方法取決於我們想知道的內容和擁有的數據類型。在本文中,我們概述了最基本和最相關的生物阻抗分析方法,以及生物阻抗領域的實例。由於生物阻抗量測通常是作為頻率掃描進行的,因此會產生大量相關且可能是多餘的數據,因此與數據縮減解決方案一起討論推論統計的含義。生物阻抗研究的目標通常是開發用於預測生物變量或狀態的方法,並概述用於開發和測試預測模型的最相關方法。
二.假設與研究設計
2.1.
研究設計
傳統方法是從量測類型作為選擇統計方法的基礎。在此,從獲取量測之前應該進行的假設和研究設計開始,以擴展了視角。原因是我們通常對於我們要通過生物阻抗量測進行研究的想法已有所了解,並且我們不會以完全隨機地進行量測。為了正確地進行調查,首先要從研究假設開始,在該假設中,我們以可檢定的方式制定需要調查的內容。例如,如果我們想要確定凝膠電極是否比紡織品電極有更低的生物阻抗測量,我們的假設可以表述為:“與使用紡織品電極相比,使用凝膠電極時,其生物阻抗更低”。我們現在有了一個可檢定的假設,我們的假設可以被實驗接受或拒絕。駁斥一個假設要比證明一個假設容易得多,因為只需要一個可靠的證據就可以拒絕它,而要證明它是正確的則需要無數的證據。這就是為什麼統計方法基於否定相反假設(稱為虛無假設)而不是嘗試證明假設的原因。在我們的例子中,我們測試了”使用凝膠電極相比使用紡織電極時,生物阻抗並不低”,這是我們的虛無假設。如果我們對測量的統計分析發現虛無假設是不可能的,則我們拒絕虛無假設,從而接受我們的原始假設。統計分析提供了一個p值,這是我們的測量結果或與虛無假設之間存在較大偏差的概率,假設虛無假設實際上是正確的。是否拒絕虛無假設基於p值是否低於預定臨界值alpha(α)(即顯著性水平)。在醫學和生物學中,α通常設置為0.05,這意味著如果我們的測量結果小於5%(假設原假設為真),我們將拒絕原假設。
上面的假設示例非常籠統,可以通過提高其專門特性來提高可測試性。如果這是我們要測試的相關設置,則“使用凝膠電極測量時,Trans-thorocic生物阻抗低於使用兩電極設置的織物電極所測量的胸阻抗”。檢定該假設較為容易,因為它僅是暗示一種特定類型的度量,並減少了得出不確定結果的機會。一個假設應該是簡單,具體且預先聲明[1]。假設決定了研究設計,我們需要進行的實驗類型,以及需要進行的量測類型。該假設主要決定哪種類型的統計檢定是合適的。例如,如果我們要調查兩種類型的組織樣本其生物阻抗是否顯著不同,則代表著我們必須評估每種類型的組織樣本其中兩組生物阻抗測量值之間的差異,並且適當的統計檢定將是對兩組中的兩種平均值進行比較的檢定,例如學生t檢定。我們還可以進行檢定力分析,以估計我們需要多少組織樣本,以便在實際存在差異的情況下有很大的機會找到差異。因此,研究的計劃應以明確的假設開始。從研究計劃到量測的統計分析的整個過程如圖1所示。
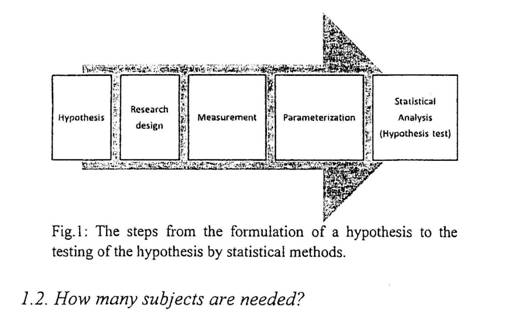
1.2.需要多少樣本?
知道需要多少單元(即項目或對象)以檢定我們的假設是一個好主意。除非我們能夠測試總體母群中的所有單位,否則我們僅能測試整個總體的樣本。為了對總體做出通用性結論,我們需要證明我們觀察到的效果不太可能是來自樣本的隨機變化。如果選擇的樣本太少,可能會導致結果不確定,研究毫無價值。選擇的樣本太多,則會浪費資源(例如犧牲過多的動物)。因此,樣本量的考慮具有倫理意義[2]。
在假設檢定中,我們希望減少兩種錯誤的機會:錯誤地拒絕一個真實的虛無假設(I型錯誤)和拒絕一個錯誤的虛無假設(II型錯誤)的機會。
I類錯誤概率由α(通常為5%)確定。對於給定的α,我們還可以計算beta(β),這是II型錯誤的概率。例如,假設您要複製對兩種材料(材料A和B)的生物阻抗所做的初步研究。您想基於t檢定來測試它們是否不同,但是您不確定是哪個樣品檢定假設所需的數目(N)。根據試驗數據,您可以估計測試材料之間的差異有多大,以及每種材料自身都有很大的差異。
以平均值為10歐姆的預期差異和標準偏差也為10歐姆為例,對於每種材料,N
= 5(對於每種材料)得出的beta為71%,這是發生II型錯誤的可能性太大。將N增加到10,我們得到44%的beta,而當N
= 20時,β降低到13%。檢定的統計檢定力為1-beta,可以當作是在假設為假時,正確拒絕原假設的能力。研究中的檢定力要求,取決於調查的類型,但通常認為檢定力>
0.8是可以接受的。
結果大小是我們正在研究的結果的相對大小。比較各組時,結果大小可能是以在各組之間|
Z |的差異,除以合併的標準偏差,或者用於測試關聯性,例如使用確定係數R2。因此,較小的效應差異量需要較大的樣本才能被檢定並且避免II型錯誤。在上面的示例中,結果大小為1(10歐姆/
10歐姆)。如果結果大小為2,只需要N
= 6即可獲得,結果為1,而N
= 20相同的檢定力。為給定的統計檢定進行樣本量估計所需的信息是:
1.
所需的α(錯誤拒絕真值的概率虛無假設)
2.
所需的β(未能拒絕錯誤的虛無空值的可能性假設)
3.
預期樣本分佈(分佈類型和差異量)
4.
預期差異或關聯的幅度。
樣本數量估計並不是一門精確的科學,通常這些輸入將是“合格的猜測”。即使如此,評估我們是否需要10或100個樣本/項目仍然很重要。我們已經根據假設決定了測試的類型,我們的α通常會設置為0.05,而beta會高於0.8。我們仍然需要提供的是結果大小。如果不知道,首先要先查詢類似的研究。也許其他研究者已經在相似的樣本上發布了具有相似量測值的數據。如果沒有以前可用的數據,則進行先期初步研究,可以用來很好地說明這些值。也許我們收集的信息表明樣本變異量可能在100到500歐姆之間,平均值之間的差異在1k到2k歐姆之間。在這種情況下,最好在確定樣本大小時考慮最壞的情況(變異量=
500歐姆,平均值之差異=
1k歐姆)。
實際上,樣本大小的計算不是人力完成的,而是電腦程序(例如免費的G
* Power©),讓您使用選擇統計檢定。軟體詢問必要的輸入(即α,β,變異量和效果大小),並為您提供所需的最小樣本量。給定樣本大小,α,β和結果的大小,它們還可以用於確定測試的檢定力。由於所有這些未知數,最好向生物統計學家諮詢這些問題。
2.3.多變量和數據約簡
通常在生物阻抗測量中,我們要檢查每個樣本或每次量測中的多個生物阻抗變量。有時,我們在研究之前對生物阻抗影響的知識知之甚少。為了最大程度地提高能夠發現變化,我們可以從一項測量在獲取多個頻率的條件下量測多個生物阻抗參數(即|
Z |,G,θ)。假設這為我們提供了100個用於比較兩種不同組織類型的變量的集合,那麼很可能我們會發現純粹由於偶然性,而在至少一個變量中存在顯著差異。對這種多重比較測試可以進行調整。例如採用
Bonferroni校正方法[3,4]。該方法通過將單比較水準除以分析中包含的多個比較次數來調整顯著性水平臨界值。對於生物阻抗分析,由於大量變數的比較,這種方法通常是不適用。除非比較次數很少,否則更好的方法是通過數據縮減或基於模型的方法來減少變量的數量。尤其是對於生物阻抗頻率掃描,這些數據通常高度相關並且可以減少為一小組變量,這些變量佔有量測中的大多數消息。生物阻抗領域中的一種常用方法是假設樣品的電學特性可以通過等效電學模型(參見5,
Chap.8)(例如Cole模型)來描述,並通過測量值來對數字模型的通稱值估算成份組(component)。有了模型和測量結果之間的良好一致性,該方法將測量結果減少為幾個不相關的參數,從而更容易進行統計處理。數據縮減也可以在沒有等效模型假設的情況下完成。減少數據的一種方法是使用主成分分析(PCA),將數據計算轉換為各組不相關的成分。該變換的工作方式是使用數據的線性組合來構造分量,這些分量盡可能解釋數據的變異量,並具有所有分量必須不相關。
PCA可以提供數據子集,通過該數據子集。幾乎所有信息(即99%)僅由幾個成份來解釋。與基於模型的方法相比,PCA的缺點在於其轉換是一個“黑匣子”。並且相對於我們要測量的內容,主要成分往往毫無物理意義。
4.統計方法的選擇
如有必要在將數據簡化為一組實際參數之後,下一步是執行統計分析。用以測試我們的原先假設是否可以被拒絕。統計方法的選擇主要由假設決定。但量測結果也可能影響最合適方法的選擇。圖2提供了根據研究類型選擇統計方法的流程圖。
4.1.
比較兩組
讓我們回到兩種組織類型的alpha參數的例示,假設兩種組織類型之間的alpha不同。自然選擇的測試是兩樣本t檢定,該檢定目的在測試兩組數據的均值是否不同,但是,如果我們的假設也考慮組織類型之間差異的方向。例如“組織A的alpha參數大於組織B的alpha參數”,則統計檢定也必須包括該正負方向。想像一下,如果我們扔出五枚硬幣,獲得所有都是正面或所有都是反面的概率為0.03,但是只要獲得所有正面或是所有反面都可以的概率為兩倍(0.06)。在第一個假設(單面)中,所有頭均具有統計學顯著性(p
<0.05)。但對於第二個假設(雙面都可)則無統計學意義。當比較兩個組的一個方向的差異時,單面(也稱為單尾)t檢定考慮了這一點。在醫學中,除非有很好的理由,否則應使用雙面假設和檢定。如果使用單面檢定,則必須事先指定檢定的方向[6]。
t檢定屬於參數檢定系列,它假設我們的數據遵循數學概率分佈,在這種情況下為常態分佈,這是在完成所有量測之前通常不知道的事情。我們的Alpha值分佈可能是不對稱的,Alpha的超重接近1,越來越少的Alpha值趨向於零。然後,我們有兩種選擇,一種是將我們的數據轉換成常態分佈,另一種是使用不需要這種分佈的統計檢定。不滿足常態分佈假設的未配對數據的另一種檢定類型是Wilcoxon
ranksum檢定(也稱為Mann-Whitney
U檢定),該檢定基於比較組內值的等級。這種類型的檢定不依賴於描述數據分佈的任何參數(例如標準差),並且屬於非參數統計檢定系列,通常處理基於數據排名的不同類型的假設檢定。
阻抗分析中,我們經常對測量值進行數學轉換,以便以不同的方式解釋或圖形化。在進行統計分析時,我們需要記住,轉換也可能會改變數據的分佈。例如當將常態分佈Z個量測值轉換為Y時,常態分佈可能會變為非常態分佈。
在前面的例子中,測量來自獨立樣本。如果我們有成對的組織類型,而且每對數據都來自同一隻動物,那麼我們就不能獨立考慮兩種組織類型的樣本,而我們必須使用統計檢定來說明每對組織中的相關性,例如成對的t-檢定或非參數Wilcoxon
Signed rank檢定。使用這些測試的典型情況是生物測試治療前後的阻抗變化。
4.2.比較兩個以上的數據組
如果我們要以統計比較兩組以上的量測值,則另一種類型的檢定更適合變方分析(ANOVA)。該測試將每個組中的變異量與組之間的變異量進行比較,並且還克服了多個成對比較的問題(如第3章所述)。變方分析具有以下假設:組與組之間的獨立性,常態分佈和組內的均等變異數。有關理論,檢定和違反這些假設的更多詳細信息,可參見文獻[7]。對於非常態數據,大多數統計軟體都提供了rank-based變方分析,而普通變方分析也被認為具有強大的功能,可以避免違反常態性假設[8]。用於比較兩個以上獨立組的單向變方分析(ANOVA)首先計算F統計量(基於組間變異性與組內變異性之間的比率),再與自由度一起確定以下項下的p值:虛無假設。假設所有組的數據均來自具有相同平均值的總體。進一步地,可以類似於t檢定來測試組間的每個成對組合之間的差異,但是需要對於多重測試進行校正。
4.3.
因子分析
當我們僅將研究量測結果的分組只有一個因素(例如不同的類型組織)時,單因子變方分析非常有用。如果我們要研究除組織類型以外,電極配置如何影響生物阻抗,我們就有兩個因子的因子設計,可以使用雙向因子變方分析。該檢定的輸出為我們提供了統計量(F統計量,p值),該統計量告訴我們那兩個因素中的那一個是否對生物阻抗都有重大影響。此外,雙因子變方分析可以測試兩個因素之間是否存在顯著的相互作用。組織類型之間其生物阻抗的差異可能取決於電極系統。作為處理兩個或兩個以上因子的程序,建議首先測試所有可能的交互作用項目。如果發現沒有顯著意義,則繼續使用無這些交互項目的ANOVA。如果存在重要的相互作用項目,則主要影響(例如組織類型和電極系統對生物阻抗的影響)可能會變得毫無意義。因為這兩種影響因子都必須受到另一個因子進行限定。在這種情況下,最合乎邏輯的方法是執行單向因子變方分析,以評估一個因素在所有水準下,而其他因子固定於一個水準(也稱為簡單效應)。如果一種或多種因子其簡單效應是顯著,則可以在給定因子水準的特定組之間,進行其他比較(例如,使用四電極系統時,組織類型A與組織類型B對比)。因子(factorial)設計和factorial
ANOVA的優點在於,它允許只有使用一部分受試者,進行單獨的實驗。就可以評估同一組假設(以同等檢定力)。以評估實驗條件之間是否有相互作用的可能性[9]。
與不成對或成對的t檢定,分別適合比較因變數和應變數組的方法是否相同。還有適用於應變數組的ANOVA方法,即重複測量repeated
measures ANOVA。考慮比較來自三個不同電極位置的生物阻抗測量值,如果所有量測都是針對不同的對象,則單向ANOVA是合適的檢定。但是,如果對每個對象進行多次量測(電極位置不同),則單向重複測量ANOVA是合適的檢定。重複量測檢定具有更高的統計檢定力,並且重複實驗設計需要的對象更少。重複測量ANOVA也可以用於因子設計(例如雙向重複量測ANOVA)和非參數數據(例如ranks
repeated measures ANOVA,Kruskal-Wallis檢定)。但是對等級執行因子ANOVA(factorial
ANOVA)時應格外小心,因為對於某些設計,或
rank轉換過程可能不穩定[10]。
在因子重複測量設計中,可以通過將時間(或重複實驗條件)作為因素納入雙因子repeated
measures ANOVA中以來研究時間的影響。重要的是要知道,變變異量分析不考慮時間點的順序的影響,而只是考慮它們之間的差異。如果我們要評估時間影響的趨勢或關係,最好使用迴歸方法。
在實驗中,可能還有除實驗因子以外的其他可觀察變量。這些變量可能會對因變量產生影響。該變量可能是連續的,因此很難在設計中添加為一個因素。在這種情況下,可以將變量作為共異變量(covariate)添加到設計中。以在不同化學反應期間,量測溶液中的阻抗為例。溫度變化可能是未知且不可控制的,但可能會影響阻抗。溫度無法將其添加為分析中的因子,而應添加為共異變量。適當的統計方法是ANCOVA(Analysis
of covariance),它是變方分析和迴歸分析組合。通過這種方法,我們在控制溫度效應的同時,發現不同化學反應的阻抗之間是否存在顯著差異。在某些情況下,我們要檢查多個因變量。如果它們是相關的,例如|
Z |和相同測量的相位,可以在同一測試中研究兩個因子變量。同時通過MANOVA(multivariate
ANOVA,
變異量的多變量分析)控制它們之間的相關性。如果因變量不相關,則適合使用單獨的變方分析。
MANOVA評估每個因子對每個因變量的影響(每種情況具有p值),以及獨立變量之間和因變量之間的相互作用。這種方法的優點是可以在一個測試中研究多個因變量,從而避免了多次比較增加的I型錯誤率,因變量之間的相關性將被納入分析中,並且該測試甚至可以找到重要的結果當所有因變量對每個因變量的影響不夠強時,將它們綜合起來。為了向MANOVA添加共異變量,合適的檢定是MANCOVA(共異變量的多變量分析),它與MANOVA相同,但是增加了對一個或多個可能影響因變量的共異變量的控制。
一種包含以上所有內容的測試(t-測試,ANOVA,ANCOVA,MANOVA和MANCOVA以及普通線性迴歸)稱為是通用線性模型(general
linear model, GLM)。該方法包含在幾個統計軟體中,是分析許多不同類型數據的便捷工具。
4.4.
混合模型
到目前為止,我們已經討論了具有固定作用的各組比較或因子分析。固定效應代表著在我們嘗試進行任何實驗複製時,我們獨立變量的水準都將相同(固定)。我們已經選擇了感興趣的某些級別,並且沒有嘗試將這些級別推廣到其他級別。例如,讓我們考慮不用電極類型的阻抗比較。我們可以進行一項研究,其目的是比較具有不同特定選擇的性能特性電極類型,電極類型將成為固定因素。我們還可以進行一項研究,其目的是評估電極類型是否對所量測的阻抗有影響。電極類型將是一個隨機因素,我們的電極類型(水準)其樣本將被視為可能電極類型/製造商總數的隨機選擇。在第一種情況下,我們的測試結果將是所選電極類型的阻抗之間的顯著差異。但是在第二種情況下,測試結果將是電極類型對阻抗的一般影響。
在某些情況下,我們的實驗可能同時包括固定因素和隨機因素,因此分析模型稱為混合效應模型。在過去的幾年中,混合模型分析方法取得了巨大的進展,並且與其他“傳統”方法相比,當前可用的統計工具具有許多不同的功能和優勢。例如,混合模型分析不會像重複Repeated
ANOVA一樣被缺失值所削弱。混合模型還可以處理數據中的層次結構。例如,我們可以研究來自不同生產商的不同電極類型的樣品,而來自每個不同生產商的電極類型也不同。用統計術語來說,我們有兩個因子(電極類型和生產廠商),其中一個因素的不同水準不會在另一個因素的所有水準上發生,這稱為巢式(Nested)(或分層)設計。混合模型方法的第三個優點是我們的量測時,不需要在相同的時間點進行。例如,如果我們在一個隨時間變化的過程中追踪不同材料的阻抗,但無法同時測量所有材料,則可以將所有量測值及其各自的時間加入到混合模型中,並檢查兩種材料類型和時間,即使每個時間點只有一個測量值。綜合所述,建議對重複(缺少值)和/或巢式(Nested)數據進行混合模型分析。這種分析可以在統計軟體(例如R,SPSS,STATA和SAS)中進行。由於選擇和設置的數量眾多,因此與ANOVA等方法相比,該過程更為先進。在開始使用混合模型之前,建議
仔細閱讀該主題或諮詢生物統計學家。
4.5.
相聯分析
到目前為止,我們一直在研究調查群體之間的差異以及不同因子對於這些差異的影響。現在,我們轉到評估變量之間相聯的方法。最基本的情況是通過皮爾遜積矩相關係數(the
Pearson product-moment correlation)檢定兩個變量之間的線性關係(也稱為雙變量關聯)。該檢定的輸出是r統計量,它表示兩個變量之間關係的強度(絕對值0-1)和方向(取決於r的正負)。R無法說明關係的因果關係或依存關係,無論X是依賴於Y還是Y是依賴於X,還是彼此獨立而又依賴於其他另一個因素,r都是相同的。
r也沒有說出X和Y之間是否有一致性。通過完全不同的尺度上的成對觀測值,您可以獲得r
= 1(完美相關)。這使得r不足以測試兩種方法之間的一致性。但是對於探索線性假設下,兩個變量之間的關聯性非常有用。
以p值和假設檢定可以對相關性進行統計推斷。r的平方也經常使用,稱為決定係數。
R2更易於解釋,尤其是對於較大的r,因為R2表示一個變量的變異數比例,該比例可以由另一變量的變易量來解釋。例如,如果我們測量BMI和全身|
Z |,並得到r
= 0.5,那麼我們可以說|
Z |的25%變異量可以由BMI解釋。
皮爾遜積矩相關係數(以及確定係數)基於變異量相等的假設(在統計術語上稱為均質變異量)。如果我們將兩個變量相對繪製,並且離散點在整個範圍內的大小,大致相同,則數據是均質性。與此相反(稱為變異性不等),相關性在兩個變量的整個範圍內將不一致。大多數統計軟體中提供了不同的均質變異量檢定。這種方法的另一個缺陷點是,它對異常值或極值十分敏感,從而導致對相關性的高估。另一個問題是,對任何一個變量範圍的限制都會直接減小r的值。通常建議從變異相互繪製開始,以研究其相關性和這些假設,並在結果發佈時提供這些圖表以及統計量(完全不同的圖可能對應於相同的r)。繪製X對Y變量圖還可以讓我們知道是否應該假定線性關係。也許因此我們看到了二次多項式關係或指數關係。在這種情況下,我們可以簡單地轉換一個變量並使用線性方法以簡化操作。如果我們不想考慮這種關係的函數,而只是測試是否存在單存相調性(兩個變量在相同或相反的方向上增加),則可以應用Spearman的等級順序相關性方法。
4.6.
迴歸方法
兩個變量之間的關係也可以在數學通過迴歸方法上描述。也許我們已經發現生物阻抗與人體總水分含量(TBW)之間存在顯著關聯,並且我們希望找到表達它們之間的公式。基本方法是簡單的線性回歸。它估計一個直線最適合相互繪製的變量,並提供該直線的截距和斜率。使用截距和斜率值,以及新的生物阻抗測量值,我們可以對TBW值做出預測。測得的TBW與預測的TBW之差稱為殘差。殘差可用於檢查所選模式(在這種情況下為線性)是否有效。殘差的散佈圖(在本例中為生物阻抗與殘差)提供了有關線性,均質變異量,常態分佈性和誤差項目相互獨立的信息,這些都是進行迴歸分析的假設。例如,如果我們看到點的分佈在x軸周圍不對稱,也稱為偏斜(Skew),則可能違反常態分配假設。這時穩健迴歸(robust
regression)方法是使用最小平方法的替代方法,可以適當地使用對於非常態分佈或有離群值存在。從殘差中,我們還可獲得了預測誤差的值,例如均方根誤差(RMSE),它是迴歸直線與所有點的接近程度的平均值。r,R2和RMSE都是評估適合程度的量度,但是RMSE更能夠告訴我們,所要預測的數量有多大的誤差。重要的是要注意,RMSE或類似的誤差值代表了我們分析過的測量樣本中的誤差,而不是整個總體。也許我們已經發現,基於生物阻抗的TBW預測的RMSE很大,如果我們要開發TBW設備,我們需要減少此誤差。我們可能知道有其他與TBW相關的因子,或是可使生物阻抗發生變化但與TBW不相關的因素(混雜變量,
confounding variables)。如果這些變量是獨立的,可以通過將其他變異作為重線性迴歸中的預測變量來減少預測誤差。例如我們可能會加上BMI和Age,並假設它們會糾正BMI和Age中的差異。
通過生物阻抗估算TBW。多元回歸為我們提供了R2和相同的誤差量,例如RMSE。同樣這些統計數據只有代表樣本而不是總體,並且針對其所基於的樣本最佳化了多重回歸的結果。隨著更多預測變量的添加,統計數據的虛假膨脹和第I型錯誤的機會增加,因此建議數據點的數量至少應為預測變量的數量的10倍[11,
p1456頁]
。建議將預測變量的數量保持較低(5個或更少),並且這些變量接近不相關,以便找到最簡單的變量其可能的預測模型。包括生物阻抗頻率掃描的所有點是多重回歸的不良預測集的一個示例。
可以根據現有的經驗數據或理論來選擇預測變量,但是也有半自動方法可以幫助篩選出多餘的預測變量。這些方法之一稱為逐步回歸,它提出了一個模型,該模型基於變量的係數估計值的t統計值連續添加或刪除變量的模型。此過程可以向前或向後。在前向過程中,變量將根據變量在預測中產生的顯著增加的程度逐一添加,直到添加的變量對迴規模式不再做出重大貢獻。向後選擇採用類似的過程,但從包含所有預測變量的模型開始。通常,正向過程最適合在很多可能的變數中找到很少的重要預測變量。而後向過程最適合消除一些變量以微調預選模型。儘管如此,仍然總是有過度擬合的機會。例如通過虛假誇大的統計數據,獲得不佳的模型,因此建議對所得迴歸模型再一次進行驗證。
對於數據例如生物阻抗頻率掃描,當我們的預測數可能比觀察數據更多。或是預測變量高度相關,這情況下其他類型的迴歸方法可能更為適合,例如主成分回歸(PCR)和偏最小平方和迴歸(PLS)。兩種方法都通過將預測變量的初始集合構建為一組新的正交(獨立)分量的線性組合,來對初始預測變量進行轉換。在PCR中,可以解釋這些預測變量的大部分變異量的主要成分都將進行主要變量回歸。通常前幾個主要成分解釋了大部分差異(通常超過90%),這些成分在PCR模型中使用。但是迴歸公式的選擇是基於包括預測變量而不是自變量的最大變異量。
PLS通過找到與因變量最相關的預測變量集的組合(通過同時分解預測變量和因變量,同時具有盡可能多地解釋之間的共變數的約束來解決此問題。對於PCR和PLS來說,選擇要包含多少個組件都是很重要的事情,並且長期以來一直是統計領域中討論的主題[12]。通常,應該使用某種交叉驗證,以便比較所包含的組件數量是否比較具有預測能力。
4.7.
分類方法
到目前為止,我們一直在處理將連續結果作為因變量的預測。假設我們已經研究了關於組織類型的生物阻抗,並發現了兩種類型的組織之間的顯著差異,現在我們要試驗如何使用生物阻抗來區分這些組織類型。Logistic回歸是這樣一種方法,它基於預測變量找到最佳模型,並為每個類別和整體類別計算正確類別的百分比。對於兩個以上的結果,另一個該方法稱為多項式邏輯回歸。其自變量可以是連續和實際數值,二變量(0或1),類別或這些類型的組合。依線性回歸計算的R2統計量對邏輯回歸適合性會有誤導性的指示,因此並提出了幾種替代類似標準[13,
ch 9.5.1]。如果結果是有序性(好good,更好better,最好best),則另一種有序邏輯回歸的變數是更合適的。邏輯回歸方法預測變量不需要為常態分佈[14,p.575]。
另一種分類方法是判別函數分析,該數學函數框架最基於與MANOVA相同的原理,而不是使用迴歸。儘管MANOVA處理的是多組之間是否在因變量方面存在顯著差異。但判別函數分析處理分佈是針對預測變量的線性組合,是否可以在組之間進行區分。其假設是預測變量為常態分佈,均質差異量,每組內所有預測變量之間有線性關係,以及預測變量中不存在多重共線性和離群值(與MANOVA相同)[9]。判別函數分析在抵制違反上述假設的情況下,通常具有相當強的強韌性,尤其是對於大樣本和每組之間數量相等的觀察值而言[9]。
生物醫學研究中使用的其他分類方法包括人工神經網絡(ANN),決策樹,支持向量機(SVM),naive貝葉斯分類器和k最近鄰方法。這些方法是機器學習領域中的重要方法。在機器學習領域中,通過從樣本數據中學習以對看不見的數據進行分類來開發研算法。這些方法在包括生物阻抗在內的生物醫學工程領域中,被越來越多地採用。
人工神經網絡是一種接受中樞神經系統啟發運作的分類方法。通過建構分層組織的互相連節點(“神經元”)網絡,通過最佳優化每個節點到節點連接的權重(代表它們之間的連接強度)來開發(也稱為訓練的)分類算法。將選定的要素其新的輸入通過網絡饋送,網絡末端的輸出層將提供建議的分類。
決策樹基利用於最大程度地分離數據的方式分割輸入數據。從而形成樹狀結構[15]。有一些可以建議樹結構的算法,例如Hunt算法。但是這些算法通常採用貪婪(greedy)策略,通過制定一系列局部最佳化決策來生長一棵樹。該方法的另一個缺點是連續變量在分拆過程中被隱性離散,從而遺失了信息[16]。
由於SVM該方法在手寫識別等問題中表現出的性能,此SVM已變得流行起來。該原理基於將數據表示為空間中的點,然後找到稱為超平面的最佳曲面,該曲面最大化了類之間的餘量。如果這些類別在原始數據空間中不是線性,而可分離的,則通過使用稱為內核技巧的數學投影將數據映射到更高維度的空間(稱為特徵空間)。在該處找到新的超平面。這使得SVM對非線性分類也很有效。
Naive貝葉斯分類使用貝葉斯定理和“Naive”獨立假設來計算類成員的概率。可以直接使用僅具有一個特徵和先驗概率的貝葉斯定理來預測班級成員資格。
例如,考慮我們正在研究以生物阻抗值作為傷口癒合的標誌。假設我們在一個實驗中收集了100個測量結果,其中有50個傷口可以自行癒合。在自行癒合的傷口中,35個其阻抗增加了。在50個未癒合的傷口中,有5個阻抗增加了。現在,我們可以計算出屬於“癒合”類別的傷口的條件概率
根據使用貝葉斯定理確定阻抗是否增加。如果阻抗增加,則為88%。如果阻抗不增加,則為25%。當包含幾個條件特徵時,由於特徵之間的關係,數學通常會出現問題,但是樸素的貝葉斯分類器假定所有特徵都是獨立的,因此易於計算。
k最近鄰居(kNN)演算法其基於該空間中k個相鄰點的已知屬性,來預測特徵空間中某個點的類別。例如假設我們要基於一組獨立的生物阻抗特徵(例如Cole參數)來預測組織狀態。使用具有已知組織狀態的測量數據集,kNN算法將首先在多維空間中構造類別標記的向量,每個特徵都具有一個維度。然後,根據到新點的距離(通常為歐幾里得距離),將基於k個最近鄰居的大多數類成員,對新度量進行類預測。這些分類方法使用不同的原理和規則來學習和預測分級資格,但通常會產生一個可以比較的結果。在文獻中說明一些方法比較[17、18]。儘管諸如SVM之類的現代方法已經表現出非常好的性能,但其缺點是該模型變成了一個難以理解的“黑匣子”,從而刪除了諸如邏輯回歸模型是量化方法。但是分類性能通常超過了對可理解模型的需求。主成分分析(PCA)已應用於基於生物阻抗測量的分類。從技術上講,PCA不算是一種分類方法,而是一種數據縮減方法,更適合作為分類分析之前的參數化步驟。
References
Hulley SB,
Cummings SR, Browner WS, Grady D, Hearst N, Newman TB. 2nd ed.
Philadelphia: Lippincott Williams and Wilkins; 2001. Getting ready to
estimate sample size: Hypothesis and underlying principles In: Designing
Clinical Research-An epidemiologic approach; pp. 51–63.
Bacchetti P,
Wolf LE, Segal MR and McCulloch CE. Ethics and sample size. Am. J.
Epidemiol. 2005;161(2):105-110.
http://dx.doi.org/10.1093/aje/kwi014
Bonferroni CE.
Teoria statistica delle classi e calcolo delle probabilit `a.
Pubblicazioni del R Istituto Superiore di Scienze Economiche e
Commerciali di Firenze. 1936;8:3-62.
Miller, RG.
Simultaneous statistical inference. 2nd ed. Springer Verlag. 1981, pp.
6-8.
http://dx.doi.org/10.1007/978-1-4613-8122-8
Grimnes S and
Martinsen ØG. Bioimpedance and Bioelectricity Basics. 2nd edition.
Academic Press. 2008.
Bland JM and
Bland DG. Statistics Notes: One and two sided tests of significance BMJ.
1994;309:248.
http://dx.doi.org/10.1136/bmj.309.6949.248
7. Dowdy S,
Wearden S and Chilko D. Statistics for research. 3rd Edition, Wiley-Interscience.
2011.
8. Schmider E,
Ziegler M, Danay E, Beyer L and Bühner M. Is it really robust?
Reinvestigating the robustness of ANOVA against violations of the normal
distribution assumption. Methodology: Europ. J. Res. Meth. Behav. Social
Sci. 2010;6:147-151.
9. Sheskin DJ.
Handbook of parametric and nonparametric statistical procedures. CRC
Press. 2011.
10.
Sawilowsky SS, Blair RC and Higgins JJ. An Investigation of the Type I
Error and Power Properties of the Rank Transform Procedure in Factorial
ANOVA. J. Educ. Stat. 1989;14:255- 267.
http://dx.doi.org/10.2307/1165018
Mariscuilo LA and
Levin JR. Multivariate statistics in the social sciences: A researcher's
guide. Brooks/Cole Pub. Co. (Monterey, California). 1983.
Peres-Neto P,
Jackson DA and Somers KM. How many principal components? Stopping rules
for determining the number of non-trivial axes revisited. Comput. Stat.
& Data Anal. 2005;49:974-997.
http://dx.doi.org/10.1016/j.csda.2004.06.015
Ryan TP. Modern
Regression Methods. 2nd ed. Wiley series in probability and statistics.
Wiley. 2008
Tabachnick BG and
Fidell LS. Using multivariate statistics (3. ed.). Pearson. New York.
1996.
Breiman L, Friedman
J, Olshen R and Stone C. Classification and Regression Trees. Belmont,
California: Wadsworth. Dowdy, Wearden, Chilko. Statistics for Research.
Wiley Series in Probability and Statistics. 1984.
Dreiseitl S
and Ohno-Machado L. Logistic regression and artificial neural network
classification models: a methodology review. J. Biomed. Inform.
2003;35:352-359.
http://dx.doi.org/10.1016/S1532-0464(03)00034-0
17. Kotsiantis SB.
Supervised Machine Learning: A Review of Classification Techniques.
Informatica. 2007;31:249-268.
18. Rani P,
Liu C, Sarkar N and Vanman E. An empirical study of machine learning
techniques for affect recognition in human-robot interaction. Pattern
Anal Applic. 2006;9:58-69.
http://dx.doi.org/10.1007/s10044-006-0025-y

|