|
https://ekja.org/journal/view.php?doi=10.4097/kja.20137
在參數統計分析方法中,經常需要滿足一些假設,例如常態性,線性關係和均變異數。從臨床情況或實驗中收集的數據經常違反這些假設。變數轉換提供了機會,使數據可用於參數統計分析而沒有統計誤差。變數轉換為有效的參數統計的分析目的及其最終目標是使用轉換後的變數完美解釋結果。變數轉換通常會更改變數單元的原始特徵和性質。逆變換對於估計結果的解釋十分重要。本文介紹有關變數轉換的一般概念,主要集中在對數轉換上。本文還介紹了逆變換和其他重要考慮因素。
介紹
大多數參數統計分析方法都需要常態性假設。當違背非常態分佈的數據奇統計結果可能是嚴重錯誤的原因。這些都是取得可靠的科學成果的明顯障礙。當樣本的大小就足夠了,即使中央極限理論可以覆蓋常態性要求,許多臨床和實驗數據仍然不能滿足正常的假設,儘管有比較大的樣本量。幸運的是,簡單的統計技術(變數轉換)提供了一種將數據分佈從非常態轉換為常態的方法。此外,變數轉換可以根據非線性關係在變數之間形成線性關係,並可以穩定線性建模中的估計變異數。
儘管變數轉換提供了一種適當的參數統計分析方法,但是對推斷結果的解釋卻是一個完全不同的問題。變數轉換會更改數據的分佈及其原始度量單位[1 ]。為了解釋這種結果或與別人比較結果,要再轉型為基本數值。統計分析始終假定alpha限制內存在允許的誤差,因為此誤差是基於概率的。當採用複雜的轉換方法時,統計分析中包括的誤差項,其反向轉換需要複雜的過程。
本文介紹了可用於醫學統計的變數變換,對數變換和逆變換的一般概念,以及冪變換的概念,特別是關於Box-Cox變換的概念。最後,描述了考慮變數轉換時的一般預防措施、每個變數的分佈以及變數之間的關係
開始統計分析,先行檢查數據的分佈狀況,變數之間的關係,遺失的數據,離群控制等這些都是統計分析和適當建模的干擾方法,這讓我們能夠克服分析過程中可能出現的問題。數據分佈和變數之間的關係決定了不適當的偏斜分佈變數。並顯示了計劃性線性迴歸的可能性。
數據分佈的形式通常在其代表名詞方面,包括平均值,中值,和表示偏離性的標準偏差(標準偏差),四分位數,範圍,最大值和最小值。另外,偏度和峰度顯示了更詳細的數據分佈形狀[2 ],大多數統計軟體提供了有關這些因素的大量資訊。如果一個變數違反常態性假設,則分佈圖或偏度/峰度可提供有關數據分佈的線索(表1)。
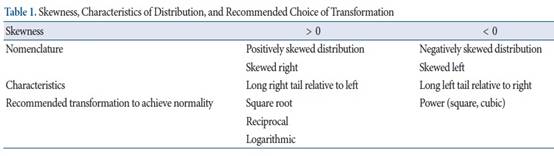
具有常態性檢定的分位數-分位數圖(QQ圖)可能暗示數據分佈偏斜[3 ]。常態分佈的數據顯示為粗糙的直線,而偏斜的數據在QQ圖上顯示為曲線(圖1)。 在臨床情況下,各種數據遵循著正或負偏斜分佈。例如,在平均動脈壓方面,大多數人有正常血壓和一些病人具有高血壓將表現更高的平均動脈壓力,而成為匯總數據的一小部分數據。來自一般人群的隨機採樣平均動脈壓數據則具有正偏分佈。Plasma
hemoglob in濃度對於普通人群則有一個負偏態分佈。
根據數據分佈的特徵,可以使用各種轉換方法來實現對常態性測試的需求(表1)。這些轉換可以使數據對稱分佈,並且偏度的絕對值接近於零[1]。這些轉換方法可以用於確保變數之間的線性關係。許多統計建模方法都是基於處理變數()和反應變數之間的線性關係,並且通過變數轉換增強明顯的線性關係作為統計模型的估計。一個典型的例子是logit變換,它用於二項式logistic迴歸。對數轉換將事件的概率轉換為對數比例,從而允許在二分結果變數和自變數之間進行迴歸分析,而自變數產生線性預測的作用。比值比可用於解釋對數變換迴歸。然而,如果使用更複雜方法進行轉換,或者如果處理()和反應變數()同時進行轉換,估計的結果解釋可能是具有挑戰性。因此轉換應盡可能簡單,以確保對統計推斷的結果進行全面的解釋。
非線性變換
通常,以加,減,乘或除一個常數進行線性變換,因為這些變換很少影響數據的分佈,它們僅根據其性質,在一定範圍上偏移幾何平均值和標準偏差。相反,包括對數變換的其他變換稱為非線性變換。它們可穩定發散,在變數之間建立線性關係,並在確保常態性假設的情況下進行參數統計估計。
儘管這些轉換方法提供了令人滿意的統計結果,但是轉換本身在解釋和報告統計結果方面構成了障礙。轉換後的變數本身有時很有意義,而無需進行反向轉換。例如某種癌症的發病率與吸煙期的平方成正比。該結果基於對觀察到的癌症發生率和吸煙時間平方的線性迴歸分析,其解釋具有意義,不需要逆變換。我們可以以中數,四分之一,四分之二區分之數據進行分析,因為原始數據違反了正常分佈的假設。如果我們比較兩個群體之間的吸煙期間數據,而數據要求平方變換以不違反常態假設,這是很難解釋平方轉換後數據的平均差異的臨床意義。每個平方值之間的差異與兩個原始數值之間的變異數差異不同。在這種情況下,非參數分析使解釋結果更加容易。
有時可能需要進行非線性變換,以符合特定統計分析(例如多元線性迴歸)的假設。如果我們對大量變數使用無關緊要的轉換方法,則很難解釋其統計估計結果。因此,對於複雜的統計分析,最好使用可解釋的轉換方法。另外,使用更自由的統計方法(例如通用線性或非線性模型)可能更合適。
對數變換
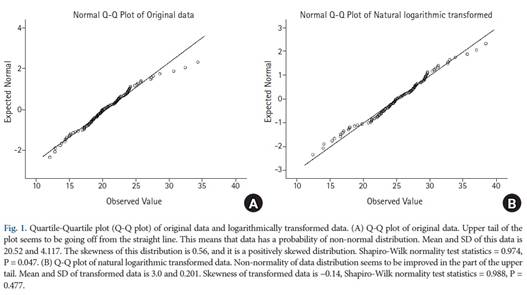
應用對數轉換,每個數值都將根據對數的特徵進行更改。考慮到其特徵,轉換後的數值之間的差異變得比原始比例值更小(圖2)。
對數變換後壓縮了數據的原始數值規模的上部和下部之間的差異。例如,對於100個案例的數據,自然對數轉換後,其偏度自0.56變為-0.14 。使用Shap iro-Wilk檢定的常態性檢定結果也將使其統計量從0.974(P
= 0.047)更改為0.988(P =
0.477)。在對數轉換後,QQ圖也趨於穩定(圖1)。如此所示,一個對數轉換對於正偏態的分佈有穩定的效果。這種轉換後的分佈稱為“對數常態分佈”。對數變換的一個有趣發現是,它的作用包括標準化後縮小數據密度和減小標準偏差 ,此後,它提供了更大的機會來滿足均勻變異數檢定,該檢定常用於各種參數統計推論。從圖1可以看出,原始數據的平均值和標準差分別為20.52和4.117,經對數變換後分別為3.0和0.201。變異係數由20.1%減少為20%。變異數係數是代表數據分佈分散性的標準化度量的代表值。較大的值表示來自數據的一個值極有可能遠離均值。通過降低標準偏差,可以滿足均勻變異數檢定的結果。並且在對數轉換變數後可以使用包括學生t檢定在內的幾種比較方法。
雖然我們可以為了預期分析而轉換數據。推斷統計數據的解釋是另一個障礙。如果我們以變換後的比例顯示推斷的數據,則不容易理解結果本身。因此,我們需要轉回數據,這是該指數轉換轉回[4 ],對於統計結果。如果我們使用自然對數變換,然後再轉回需要自然指數函數。這種計算簡單,但解釋十分困難。對數轉換的平均值應轉換為指數標度。原始數據轉回的數據分別為20.53和e(3.00)
= 20.09,(圖1)。平均值20.09,稱為幾何平均值,是來自轉換數據平均值的逆轉換。與相應的原數據算術平均值相比,幾何平均值受到原始數據值的影響較小,後者來自偏斜分佈。從估計值轉回原始值,其對標準偏差應該考慮。但是,就轉回逆變換而言,“標準”偏差的含義失去了其累加含義,因為此類數據不是常態分佈[5 ]。在轉回逆變換之後,其解釋沒有意義。因此,通常針對這種情況報告其信賴區間(CI)[ 4,6 ]。轉回變換的CI可以更好地理解原始數據。例如,樣本數為100的數據自然對數後再轉換數據的平均值和標準偏差為3.00和0.201。其原始數據95%CI為2.96至3.03。使用指數函數執行轉回變換時,它會從變為19.31~20.89。考慮到幾何平均值為20.09,轉回逆變換後的95%CI來自於幾何平均值轉換,因此不具有對稱位置。有時我們會使用帶有轉換形式的變數。轉回轉換對於統計分析是必不可少的,並且在報告結果時應恢復到原始數值。一個例子是抗體效價。如果一個重症病人肌無力測試為anticho陽性與抗體滴度1:32,這代表著數據應重複五次,抗體效價本身俱有稀釋數冪值的特徵,通常以1:2(稀釋數目)報告。因此幾何平均值應表現為2(mean稀釋數),不能使用滴度平均值。
此外,當使用對數變換時,從t檢定獲得的平均值差異並不表示估計值平均值之間的差異。由於對數轉換值再轉回原始值,導致轉換值差異是一種比例值。與兩個自然對數轉換值後的樣本的平均差為X1
–X2,轉回原始數值之差異為Exp(X1-X2)=Exp(X1)-Exp(X2),對數變換後的平均值差異應解釋為轉回原始數值之平均比例值。例如,如果平均值差異為0.5,Exp(0.5)
= 1.65。代表一個樣品平均值,相比於另一個平均值具有65%的更高值。這不應解釋為165%,我們應該考慮此差異,不是一個簡單的比例值。平均值差異的CI也可以用類似的方式解釋。如果上述樣本的95%CI的估計值為0.4–0.6,則轉回變換範圍為1.49–1.83,則其解釋為“來自一個樣本的平均值為為一樣本的65%較高值。而其95%CI的範圍與其他樣本平均值相為49%至83”
%比。” 可以使用對數轉換後的數據來估算報告統計資訊。報告此資訊時,應隨附有關轉換的資訊。相應的檢定力大小和P值也可以報告為估計值。這種解釋方法可以應用於平均值比較的統計方法。
皮爾遜的相關分析和線性迴歸分析也需要常態性數據。當對數轉換應用於前者的數據時,結果可以描述為估計值。相關係數是具有效應大小特徵的統計量,我們不需要進行進一步的轉回變換。報告有關轉換資訊的結果只需要做一件事。如果將對數變換用於線性迴歸,則在結果解釋方面會產生更複雜的考慮。線性迴歸需要符合幾個假設,包括自變數和因變數之間的線性關係。為了實現這一設想,變數變換可能是需要。如果因變數需要對數轉換,則迴歸係數的含義將從單位更改變為比例。基本上,迴歸係數的定義是“自變數的一個單位變化導致因變數因迴歸係數的增加或減少”。變換後的因變數的算術增量或減量將隨著指數函數的轉回變換而改變為比例。例如,迴歸係數的估計值為0.1,Exp(0.1) =
1.105,其意思是“在獨立變數,增加一個單位,因變數增加10.5%” 與平均差的解釋類似。應注意的是解釋值不是110.5%。如果因變數是普通對數轉換變數,則獨立變數的一個單位變化與原始數據的十倍增加量相同。即自變數有十倍增加量,由迴歸係數估計值加以改變。也可以以自變數增加1%描述。為方便起見,普通對數轉換最好應用於自變數(Yi)轉換。如果應用自然對數轉換,以e為自然對數的基礎很難進行解釋。所述似值為2.71828。如果與都以對數變換來變換,我們可以解釋為獨立變數()的百分比增量產生因變數()的百分位數變化。這些解釋規則可以應用於另一種通用線性建模方法,包括ANCOVA和MANOVA。
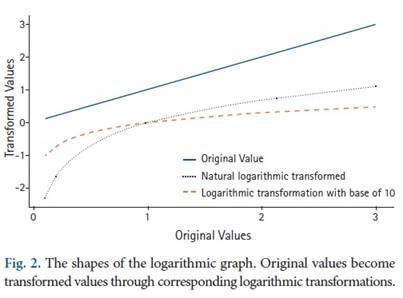
關於對數轉換有幾個問題報告 [7 ]。當原始數值負或零時,則無法進行這種轉換。為了克服這個問題,增加一個正的常數於原始數據是一個比較方使的做法。然而對數圖的形狀在早期從零微妙地改變,然後在後段進入流暢的曲線部分(圖2)。對數變換後的數據的離散度可以根據來自原始定標數據的增加值而變化。例如假設使用隨機創建函數,兩個常態分佈數據一組平均值=
0,標準偏差 = 1,n = 100。另一組平均值=
1,標準偏差 = 3,n = 100。然後,我們添加一個正數使所有的數據都為正,再以10為底的對數變換所有數據集。然後,將它們的平均值和標準偏差繪製在一張圖中,我們可以看到平均值差和標準偏差隨著添加的正數值的增加而變小(圖3)。作為重新統計結果的估計t值和P值也發生變化。當兩組數據平均值差和標準偏差都比較小,但因使用添加正值再進行轉換,估計統計量可能增加。因為即使平均差異和標準偏差都很大,其檢定結果附加值增加。這些類型的錯誤來自因為對數轉換產生的改變。當值較小時,它會增加差異。當值較大時,它會減小差異。從虛假設顯著性檢定的角度來看,除非t統計量非常接近顯著性水準,否則t檢定的顯著性可能不會改變。但是,應注意的是,由於對數轉換可穩定標準偏差值,因此估算的統計量和執行的檢定力也會發生變化。
乘冪變換和Box-Cox變換
冪變換是一種使用冪函數的變換方法。如果我們使用大於1的數字作為冪函數的指引,則它可以將左偏數據轉換為近乎正常分佈的數據。有一種特別的冪轉換稱為Box-Cox變換[8 ],這是經常使用以穩定線性迴歸或相關性分析以穩定變異誤差。Box-Cox變換有幾種擴展形式[9 ],傳統方法如在下面的(等式1)中擁有。
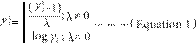
根據λ的值,它執行各種類型的非線性變換。例如,λ=
-1產生到數變換,λ= 2產生平方變換,而λ =
0.5產生平方根變換。因為它包含一個常數,所以也應用了某種程度的線性變換,因為我們已經知道線性變換幾乎不會影響估計的統計量。但是,我們應該注意這種轉換可能會影響統計結果,如上一節所述。如果λ=
0,則Box-Cox變換與對數變換相同。那麼,我們如何確定λ的值以及Box-Cox變換如何穩定變異數呢?我們如果考慮使用線性迴歸。線性迴歸需要的假設包括均勻變異數。這代表著所有觀測值都是從估計迴歸線中均勻分散。一些殘差圖的診斷法提供了有關均勻變異數的資訊。當違反均勻變異量時,Box-Cox變換可以穩定殘差的變異數。使用的yλ代替線性迴歸模型y,例如,yλ=αX+β+ε(α:迴歸係數,β:常數,ε:誤差)。有幾個統計軟體程式可用以找到λ的最佳估計值,並基於最大似然法計算95%CI。使用這個結果,我們可以得到具有均等變異量的線性迴歸模型。雖然Box-Cox變換是一個很好的工具,可以得到線性迴歸的最好的結果,但是它也有一個嚴重的概率結果解釋的問題。其轉回反向轉換不像其他非線性轉換那樣簡單,因為它包含誤差項,該誤差項對於線性迴歸至關重要。有一些自Box-
Cox變換轉回的幾個提議方法[10,11 ],這需要複雜的統計過程。如果嘗試將其解釋為轉換後的變數本身,則還應考慮轉換後的單位,經轉換後的單位可能會失去其真實含義。只有在當其他用於穩定變異數(均變異數)的措施失敗時,才應考慮Box-Cox變換。
結論
參數統計分析經常用於醫學研究。不幸的是,許多醫學研究者還沒有認識到這些分析方法需要數據常態分佈和其他假設。還有許多其他具有更寬泛假設的分析方法,例如通用線性或非線性模型。但是,我們需要簡化和直觀的分析,包括t檢定和變異數分析(ANOVA)。變數轉換是使數據呈常態分佈或形成數據線性關係的強大工具。然而,最重要的轉換數據應轉回轉化成為可解釋的結果。轉換可能很容易,可以在常用的電子表格程式中計算轉換。但是,如果使用複雜的轉換或多個轉換的組合,則轉回轉換並非易事。結果解釋還取決於轉換後的變數的作用。轉化的獨立變數相對簡單(yi)用以解釋。當對因變數(xi)進行轉換時,轉向轉換應依賴於轉換後的誤差項。變數變換提供啟用參數統計分析的一個有吸引力的和方便的方法,和數據的準備應該優先考慮。有關數據分佈的信息(例如偏度,範圍,均值,標準偏差,中位數和四分位數)以及變數之間的關係(散點圖)可用於得出最佳方法。離群值控制,遺失的數據評價和樣本大小的充足應當優先考慮於變數變換之前。如果可能的話,使用統計分析與通用假設是一個選項,非參數統計分析也可保證了科學的結果。 |